logistic map

The logistic map is a discrete dynamical system defined by the quadratic difference equation:

Equivalently it is a recurrence relation and a polynomial mapping of degree 2. It is often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple nonlinear dynamical equations.

The map was initially utilized by Edward Lorenz in the 1960s to showcase properties of irregular solutions in climate systems. It was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation written down by Pierre François Verhulst.
Other researchers who have contributed to the study of the logistic map include Stanisław Ulam, John von Neumann, Pekka Myrberg, Oleksandr Sharkovsky, Nicholas Metropolis, and Mitchell Feigenbaum.

Two introductory examples

Dynamical Systems example

In the logistic map, x is a variable, and r is a parameter. It is a map in the sense that it maps a configuration or phase space to itself (in this simple case the space is one dimensional in the variable x)

$$$$

It can be interpreted as a tool to get next position in the configuration space after one time step. The difference equation is a discrete version of the logistic differential equation, which can be compared to a time evolution equation of the system.

Given an appropriate value for the parameter r and performing calculations starting from an initial condition $x_0$, we obtain the sequence $x_0$, $x_1$, $x_2$, .... which can be interpreted as a sequence of time steps in the evolution of the system.

In the field of dynamical systems, this sequence is called an orbit, and the orbit changes depending on the value given to the parameter. When the parameter is changed, the orbit of the logistic map can change in various ways, such as settling on a single value, repeating several values periodically, or showing non-periodic fluctuations known as chaos.

Another way to understand this sequence is to iterate the logistic map (here represented by $f(x)$) to the initial state $x_0$

$\begin x_&=f(x_)\\ x_&=f(x_1)=f(f(x_))\\ x_&=f(x_2)=f(f(f(x_)))\\ x_&=...\\ \end$

Now this is important given this was the initial approach of Henri Poincaré to study dynamical systems and ultimately chaos starting from the study of fixed points or in other words states that do not change over time (i.e. when $x_n=...=x_1=x_0=f(x_0)$). Many chaotic systems such as the Mandelbrot set emerge from iteration of very simple quadratic nonlinear functions such as the logistic map.

Demographic model example

Taking the biological population model as an example is a number between zero and one, which represents the ratio of existing population to the maximum possible population.
This nonlinear difference equation is intended to capture two effects:
* ''reproduction'', where the population will increase at a rate proportional to the current population when the population size is small,
* ''starvation'' (density-dependent mortality), where the growth rate will decrease at a rate proportional to the value obtained by taking the theoretical "carrying capacity" of the environment less the current population.

The usual values of interest for the parameter are those in the interval , so that remains bounded on . The case of the logistic map is a nonlinear transformation of both the bit-shift map and the case of the tent map. If , this leads to negative population sizes. (This problem does not appear in the older Ricker model, which also exhibits chaotic dynamics.) One can also consider values of in the interval , so that remains bounded on .

Characterization of the logistic map

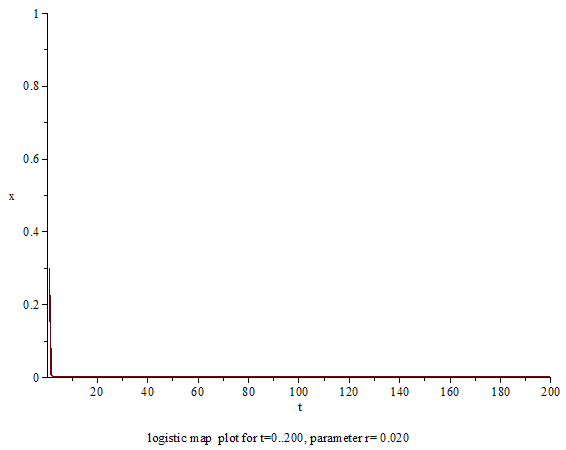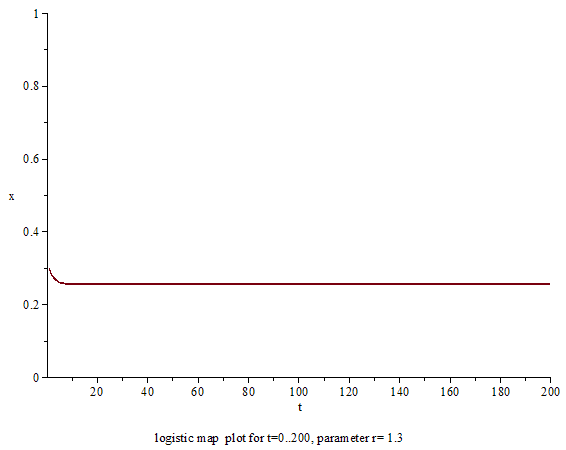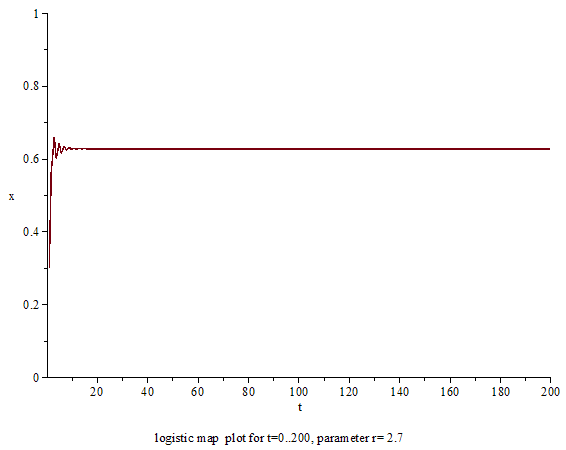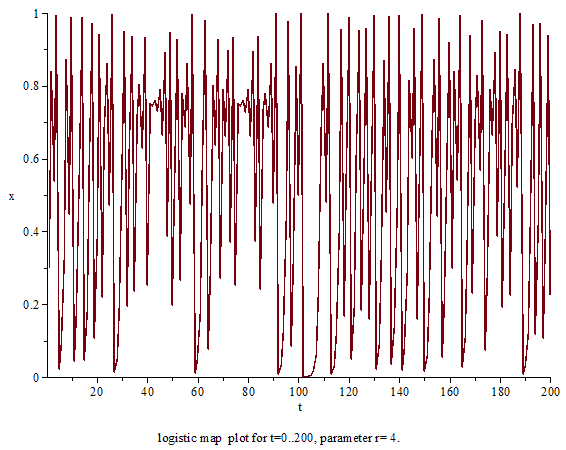The animation shows the behaviour of the sequence $x_n$ over different values of the parameter r. A first observation is that the sequence does not diverge and remains finite for r between 0 and 4. It is possible to see the following qualitative phenomena in order of time:
* exponential convergence to zero
* convergence to a non-zero fixed value (see Exponential function or Characterizations of the exponential function point 4)
* initial oscillation and then convergence (see Damping and Damped harmonic oscillator)
* stable oscillations between two values (see Resonance and Simple harmonic oscillator)
* growing oscillations between a set of values which are multiples of two such as 2,4,8,16 etc. (see Period-doubling bifurcation)
* Intermittency (i.e. sprouts of oscillations at the onset of chaos)
* fully developed chaotic oscillations
* topological mixing (i.e. the tendency of oscillations to cover the full available space).

The first four are also available in standard linear systems, oscillations between two values are available too under resonance, chaotic systems though have typically a large range of resonance conditions.
The other phenomena are peculiar to chaos. This progression of stages is strikingly similar to the onset of turbulence.
Chaos is not peculiar to non-linear systems alone and it can also be exhibited by infinite dimensional linear systems.

As mentioned above, the logistic map itself is an ordinary quadratic function. An important question in terms of dynamical systems is how the behavior of the trajectory changes when the parameter changes. Depending on the value of , the behavior of the trajectory of the logistic map can be simple or complex. Below, we will explain how the behavior of the logistic map changes as increases.

Domain, graphs and fixed points

As mentioned above, the logistic map can be used as a model to consider the fluctuation of population size. In this case, the variable x of the logistic map is the number of individuals of an organism divided by the maximum population size, so the possible values of x are limited to 0 ≤ x ≤ 1. For this reason, the behavior of the logistic map is often discussed by limiting the range of the variable to the interval , 1

If we restrict the variables to 0 ≤ x ≤ 1, then the range of the parameter r is necessarily restricted to 0 to 4 (0 ≤ r ≤ 4). This is because if $x_n$ is in the range , 1 then the maximum value of $x_$ is
r/4. Thus, when r > 4, the value of $x_$ can exceed 1. On the other hand, when r is negative, x can take negative values.

A graph of the map can also be used to learn much about its behavior. The graph of the logistic map $x_= r x (1-x_n)$ is the plane curve that plots the relationship between $x_n$ and $x_$, with $x_n$ (or x) on the horizontal axis and $x_$ (or f (x)) on the vertical axis. The graph  of the logistic map looks like this, except for the case r = 0:

It has the shape of a parabola with a vertex at

When r is changed, the vertex moves up or down, and the shape of the parabola changes. In addition, the parabola of the logistic map intersects with the horizontal axis (the line where $x_ = 0$) at two points. The two intersection points are $(x_n, x_) = (0,0)$ and $(x_n, x_) = (1,0)$, and the positions of these intersection points are constant and do not depend on the value of r.

Graphs of maps, especially those of one variable such as the logistic map, are key to understanding the behavior of the map. One of the uses of graphs is to illustrate fixed points, called points. Draw a line y = x (a 45° line) on the graph of the map. If there is a point where this 45° line intersects with the graph, that point is a fixed point. In mathematical terms, a fixed point is

It means a point that does not change when the map is applied. We will denote the fixed point as $x_f$. In the case of the logistic map, the fixed point that satisfies equation (2-2) is obtained by solving $rx (1 - x)= x$.

(except for r = 0). The concept of fixed points is of primary importance in discrete dynamical systems.

Another graphical technique that can be used for one-variable mappings is the spider web projection. After determining an initial value $x_0$ on the horizontal axis, draw a vertical line from the initial value $x_0$ to the curve of f(x). Draw a horizontal line from the  point where the curve of f(x) meets the 45° line of y = x, and then draw a vertical line from the point where the curve meets the 45° line to the curve of f(x). By repeating this process, a spider web or staircase-like diagram is created on the plane. This construction is in fact equivalent to calculating the trajectory graphically, and the spider web diagram created represents the trajectory starting from $x_0$. This projection allows the overall behavior of the trajectory to be seen at a glance.

Behavior dependent on

The image below shows the amplitude and frequency content of a logistic map that iterates itself for parameter values ranging from 2 to 4. Again one can see initial linear behaviours then chaotic behaviour not only in the time domain (left) but especially in the frequency domain or spectrum (right), i.e. chaos is present at all scales as it is in the case of Energy cascade of Kolmogorov and it even propagates from one scale to another.

By varying the parameter , the following behavior is observed:

Case when 0 ≤ r < 1

First, when the parameter r = 0, $x_1 = 0$, regardless of the initial value $x_0$. In other words, the trajectory of the logistic map when a = 0 is a trajectory in which all values after the initial value are 0, so there is not much to investigate in this case.

Next, when the parameter r is in the range 0 < r < 1, $x_n$ decreases monotonically for any value of $x_0$ between 0 and 1. That is, $x_n$ converges to 0 in the limit n → ∞.
The point to which $x_n$ converges is the fixed point $x_$ shown in equation (2-3). Fixed points of  this type, where orbits around them converge, are called asymptotically stable, stable, or attractive. Conversely, if orbits around $x_f$ move away from $x_f$ as time n increases, the fixed point $x_f$ is called unstable or repulsive.

A common and simple way to know whether a fixed point is asymptotically stable is to take the derivative of the map f. This derivative is expressed as $f'(x)$,
$x_f$ is asymptotically stable if the following condition is satisfied.

We can see this by graphing the map: if the slope of the tangent to the curve at $x_f$ is between −1 and 1, then $x_f$ is stable and the orbit around it is attracted to $x_f$. The derivative of the logistic map is

Therefore, for x = 0 and 0 < r < 1, 0 < f  '(0) < 1, so the fixed point $x_$ = 0  satisfies equation (3-1).

However, the discrimination method using equation (3-1) does not know the range of orbits from $x_f$ that are attracted to $x_f$. It only guarantees that x within a certain neighborhood of $x_f$ will converge. In this case, the domain of initial values that converge to 0 is the entire domain , 1 but to know this for certain, a separate study is required.

The method for determining whether a fixed point is unstable can be found by similarly differentiating the map. For r<1 if a fixed point $x_f$ is unstable if

If the parameter lies in the range 0 < r < 1, then the other fixed point $x_ = 1 - 1/a$
is negative and therefore does not lie in the range , 1 but it does exist as an unstable fixed point.

Case when 1 ≤ r ≤ 2

In the general case with between 1 and 2, the population will quickly approach the value , independent of the initial population.

When the parameter r = 1, the trajectory of the logistic map converges to 0 as before, but the convergence speed is slower at r = 1. The fixed point 0 at r = 1 is asymptotically stable, but does not satisfy equation (3-1). In fact, the discrimination method based on equation (3-1) works by approximating the map to the first order near the fixed point. When r = 1, this approximation does not hold, and stability or instability is determined by the quadratic (square) terms of the map, or in order words the second order perturbation.

When r = 1 is graphed, the curve is tangent to the 45° diagonal at x = 0. In this case, the fixed point $x_ = 1 - 1/r$, which exists in the negative range for $0 < r < 1$, is $x_=0$.
For $x_ = 0$, that is, as r increases, the value of $x_$ approaches 0, and just at r = 1  , $x_$ collides with  $x_ = 0$. This collision gives rise to a phenomenon known as a transcritical bifurcation.
Bifurcation is a term used to describe a qualitative change in the behavior of a dynamical system. In this case, transcritical bifurcation is when the stability of fixed points alternates between each other. That is, when r is less than 1, $x_$ is stable and $x_$ is unstable, but when r is greater than 1, $x_$ is unstable and $x_$ is stable. The parameter  values at which bifurcation occurs are called bifurcation points. In this case, r = 1 is the bifurcation point.

As a result of the bifurcation, the orbit of the logistic map converges to the limit point $x_ = 1 - 1/r$ instead of $x_ = 0$. In particular, if the parameter $1 < r \le 2$, then the trajectory starting from a value $x_0$in the interval (0, 1), exclusive of 0 and 1, converges to $x_$ by increasing or decreasing monotonically. The difference in the convergence pattern depends on the range of the initial value. $0 < x_0 < 1 - 1/r$

In the case of $1 - 1/r< x_0 < 1/r$
Then, it converges monotonically,
$1/r< x_0 < 1$, the function converges monotonically except for the first step.

Furthermore, the fixed point $x_ = 0$ becomes unstable due to bifurcation, but continues to exist as a fixed point even after r > 1. This does not mean that there is no initial value other than $x_$ itself that  can reach this unstable fixed point  $x_$. This is $x_0 = 1$, and since the logistic map satisfies f (1) = 0 regardless of the value of r,  applying the map once to $x_0 = 1$ maps it to $x_ = 0$. A point such as x = 1 that can be reached directly as a fixed point by a  finite number of iterations of the map is called a final fixed point.

Case when 2 ≤ r ≤ 3

With between 2 and 3, the population will also eventually approach the same value , but first will fluctuate around that value for some time. The rate of convergence is linear, except for , when it is dramatically slow, less than linear (see Bifurcation memory).

When the parameter 2 < r < 3, except for the initial values 0 and 1, the fixed point $x_ = 1 - 1/r$ is the same as when 1 < r ≤ 2.
However, in this case the convergence is not monotonically. As the variable approaches $x_$, it becomes larger and smaller than $x_$ repeatedly, and follows a convergent trajectory that oscillates around $x_$.

. The value that is mapped to $x_$ by applying the mapping once is $f(\tilde_) = x_$
-->

In general, bifurcation diagrams are useful for understanding bifurcations. These diagrams are graphs of fixed points (or periodic points, as described below) x as a function of a parameter a, with a on the horizontal axis and x on the vertical axis. To distinguish between stable and unstable fixed points, the former curves are sometimes drawn as solid lines and the latter as dotted lines. When drawing a bifurcation diagram for the logistic map, we have a straight line representing the fixed point $x_ = 0$  and a straight line representing the fixed point $x_ = 1-1/a$
It can be seen that the curves representing a and b intersect at r = 1, and that stability is switched between the two.

Case when 3 ≤ r ≤ 3.44949

In the general case With between 3 and 1 +  ≈ 3.44949 the population will approach permanent oscillations between two values. These two values are dependent on and given by $x_=\frac\left(r+1\pm\sqrt\right)$.

When the parameter is exactly r = 3, the orbit also has a fixed point $x_ = 1-1/r$.
However, the variables converge more slowly than when $2 < r < 3$. When $r = 3$, the derivative $f'(x_)$ reaches −1 and no longer satisfies equation (3-1). When r exceeds 3, $f'(x_)<-1$, and $x_$ becomes  an unstable fixed point. That is, another bifurcation occurs at $r = 3$.

For $r = 3$ a type of bifurcation known as a period doubling bifurcation occurs. For $r > 3$, the orbit no longer converges to a single point, but instead alternates between large and small values even after a sufficient amount of time has passed. For example, for $r = 3.3$, the variable alternates between the values 0.4794... and 0.8236....

An orbit that cycles through the same values periodically is called a periodic orbit. In this case, the final behavior of the variable as n → ∞ is a periodic orbit with two periods. Each value (point) that makes up a periodic orbit is called a periodic point. In the example where a = 3.3, 0.4794... and 0.8236... are periodic points. If a certain x is a periodic point, then in the case of two periodic points, applying the map twice to x will return it to its original state, so

If we apply the logistic map equation (1-4) to this equation, we get

This gives us the following fourth-order equation. The solutions of this equation are the periodic points. In fact, there are two fixed points $x_ = 0$ and $x_ = 1 - 1/a$
also satisfies equation (3-4). Therefore, of the solutions to equation (3-5), two correspond to $x_$ and $x_$, and the remaining two solutions are 2-periodic points. Let the 2-periodic points be denoted as $x^_$ and $x^_$, respectively. By solving equation (3-5), we can obtain them as follows

A similar theory about the stability of fixed points can also be applied to periodic points. That is, a periodic point that attracts surrounding orbits is called an asymptotically stable periodic point, and a periodic point where the surrounding orbits move away is called an unstable periodic point. It is possible to determine the stability of periodic points in the same way as for fixed points. In the general case, consider $f^k(x)$ after k iterations of the map.
Let $(f^k)'(x)$ be the derivative  $df^k(x)/dx$ of the k-periodic point $x^_f$. If $x^_f$ satisfies:

then $x^_f$ is asymptotically stable.

then $x^_f$ is unstable.

The above discussion of the stability of periodic points can be easily understood by drawing a graph, just like the fixed points. In this diagram, the horizontal axis is xn and the vertical axis is $x_$, and a curve is drawn that shows the relationship between $x_$ and $x_n$. The intersections of this curve and the 45° line are points that satisfy equation (3-4), so the intersections represent fixed points and 2-periodic points. If we draw a graph of the logistic map $f^2(x)$, we can observe that the slope of the tangent at the fixed point $x_$ exceeds  1 at the boundary $r=3$ and becomes unstable. At the same time, two new intersections appear, which are the periodic points $x^_$ and $x^_$.

When we actually calculate the differential coefficients of two periodic points for the logistic map, we get

When this is applied to equation (3-7), the parameter a becomes:

It can be seen that the 2-periodic points are asymptotically stable when this range is $3 < r < 1 + \sqrt$, i.e., when r exceeds $1 + \sqrt = 3.44949...$, the 2-periodic points are no longer asymptotically stable and their behavior changes.

Almost all initial values in , 1are attracted to the 2-periodic points, but $x_= 0$ and $x_ = 1 - 1/a$
remains as an unstable fixed point in ,1 These unstable fixed points continue to remain in ,1even if r is increased. Therefore, when the initial value is exactly $x_$ or $x_$, the orbit  does not attract to a 2-periodic point. Moreover, when the initial value is the final fixed point for $x_$ or the final fixed point for $x_$, the orbit does not attract to a 2-periodic point. There are an infinite number of such final fixed points in , 1 However, the number of such points is negligibly small compared to the set of real numbers 0, 1

Case when 3.44949 ≤ r ≤ 3.56995

With between 3.44949 and 3.54409 (approximately), from almost all initial conditions the population will approach permanent oscillations among four values. The latter number is a root of a 12th degree polynomial .

With increasing beyond 3.54409, from almost all initial conditions the population will approach oscillations among 8 values, then 16, 32, etc. The lengths of the parameter intervals that yield oscillations of a given length decrease rapidly; the ratio between the lengths of two successive bifurcation intervals approaches the Feigenbaum constant . This behavior is an example of a period-doubling cascade.

When the parameter r exceeds $1 + \sqrt = 3.44949...$, the previously stable 2-periodic points become unstable, stable 4-periodic points are generated, and the orbit gravitates toward a 4-periodic oscillation. That is, a period-doubling bifurcation occurs again at $r = 3.44949...$. The value of x at the 4-periodic point is also

satisfies, so that solving this equation allows the values of x at the 4-periodic points to be found. However, equation (3-11) is a 16th-order equation, and even if we factor out the four solutions for the fixed points and the 2-periodic points, it is still a 12th-order equation. Therefore, it is no longer possible to solve this equation to obtain an explicit function of a that represents the values of the 4-periodic points in the same way as for the 2-periodic points.

As a becomes larger, the stable 4-periodic point undergoes another period doubling, resulting in a stable 8-periodic point. As an increases, period doubling bifurcations occur infinitely: 16, 32, 64, ..., and so on, until an infinite period, i.e., an orbit that never returns to its original value. This infinite series of period doubling bifurcations is called a cascade. While these period doubling bifurcations occur infinitely, the intervals between a at which they occur decrease in a geometric progression. Thus, an infinite number of period doubling bifurcations occur before the parameter a reaches a finite value. Let the bifurcation from period 1 to period 2 that occurs at r = 3 be counted as the first period doubling bifurcation. Then, in this cascade of period doubling bifurcations, a stable 2k-periodic point occurs at the k-th bifurcation point. Let the k-th bifurcation point a be denoted as a k. In this case, it is known that $r_k$ converges to the following value as k → ∞.

Furthermore, it is known that the rate of decrease of a k reaches a constant value in the limit, as shown in the following equation.

This value of δ is called the Feigenbaum constant because it was discovered by mathematical physicist Mitchell Feigenbaum. a∞ is called the Feigenbaum point. In the period doubling cascade, $f^m$  and $f^$ have the property that they are locally identical after an appropriate scaling transformation. The Feigenbaum constant can be found by a technique called renormalization that exploits this self-similarity. The properties that the logistic map exhibits in the period doubling cascade are also universal in a broader class of maps, as will be discussed later. 

To get an overview of the final behavior of an orbit for a certain parameter, an approximate bifurcation diagram, orbital diagram, is useful. In this diagram, the horizontal axis is the parameter r and the vertical axis is the variable x, as in the bifurcation diagram. Using a computer, the parameters are determined and, for example, 500 iterations are performed. Then, the first 100 results are ignored and only the results of the remaining 400 are plotted. This allows the initial transient behavior to be ignored and the asymptotic behavior of the orbit remains. For example, when one point is plotted for r, it is a fixed point, and when m points are plotted for r, it corresponds to an m-periodic orbit. When an orbital diagram is drawn for the logistic map, it is possible to see how the branch representing the stable periodic orbit splits, which represents a cascade of period-doubling bifurcations.

When the parameter $r = r_$ is exactly the accumulation point of the period-doubling cascade, the variable $x_n$ is attracted to aperiodic orbits that never close. In other words, there exists a periodic point with infinite period at $r_$. This aperiodic orbit is called the Feigenbaum attractor. The critical $2^$ attractor. An attractor is a term used to refer to a region that has the property of attracting surrounding orbits, and is the orbit that is eventually drawn into and continues. The attractive fixed points and periodic points mentioned above are also members of the attractor family.

The structure of the Feigenbaum attractor is the same as that of a fractal figure called the Cantor set. The number of points that compose the Feigenbaum attractor is infinite and their cardinality is equal to the real numbers. However, no matter which two of the points are chosen, there is always an unstable periodic point between them, and the distribution of the points is not continuous. The fractal dimension of the Feigenbaum attractor, the Hausdorff dimension or capacity dimension, is known to be approximately 0.54.

Case when 3.56995 < r < 4

= Qualitative Summary

=

* At is the onset of chaos, at the end of the period-doubling cascade. From almost all initial conditions, we no longer see oscillations of finite period. Slight variations in the initial population yield dramatically different results over time, a prime characteristic of chaos.
* This number shall be compared and understood as the equivalent of the Reynolds number for the onset of other chaotic phenomena such as turbulence and similar to the critical temperature of a phase transition. In essence the phase space contains a full subspace of cases with extra dynamical variables to characterize the microscopic state of the system, these can be understood as Eddies in the case of turbulence and order parameters in the case of phase transitions.
* Most values of beyond 3.56995 exhibit chaotic behaviour, but there are still certain isolated ranges of that show non-chaotic behavior; these are sometimes called ''islands of stability''. For instance, beginning at 1 +  (approximately 3.82843) there is a range of parameters that show oscillation among three values, and for slightly higher values of oscillation among 6 values, then 12 etc.
* At $r = 1 + \sqrt 8 = 3.8284...$, the stable period-3 cycle emerges.
* The development of the chaotic behavior of the logistic sequence as the parameter varies from approximately 3.56995 to approximately 3.82843 is sometimes called the Pomeau–Manneville scenario, characterized by a periodic (laminar) phase interrupted by bursts of aperiodic behavior. Such a scenario has an application in semiconductor devices. There are other ranges that yield oscillation among 5 values etc.; all oscillation periods occur for some values of . A ''period-doubling window'' with parameter is a range of -values consisting of a succession of subranges. The th subrange contains the values of for which there is a stable cycle (a cycle that attracts a set of initial points of unit measure) of period . This sequence of sub-ranges is called a ''cascade of harmonics''. In a sub-range with a stable cycle of period , there are unstable cycles of period for all . The value at the end of the infinite sequence of sub-ranges is called the ''point of accumulation'' of the cascade of harmonics. As rises there is a succession of new windows with different values. The first one is for ; all subsequent windows involving odd occur in decreasing order of starting with arbitrarily large .
* At $r = 3.678..., x = 0.728...$, two chaotic bands of the bifurcation diagram intersect in the first Misiurewicz point for the logistic map. It satisfies the equations $r^3 - 2r^2 - 4r -8 = 0, x = 1-1/r$.
* Beyond , almost all initial values eventually leave the interval and diverge. The set of initial conditions which remain within form a Cantor set and the dynamics restricted to this Cantor set is chaotic.

For any value of there is at most one stable cycle. If a stable cycle exists, it is globally stable, attracting almost all points. Some values of with a stable cycle of some period have infinitely many unstable cycles of various periods.

The bifurcation diagram at right summarizes this. The horizontal axis shows the possible values of the parameter while the vertical axis shows the set of values of visited asymptotically from almost all initial conditions by the iterates of the logistic equation with that value.

The bifurcation diagram is a self-similar: if we zoom in on the above-mentioned value and focus on one arm of the three, the situation nearby looks like a shrunk and slightly distorted version of the whole diagram. The same is true for all other non-chaotic points. This is an example of the deep and ubiquitous connection between chaos and fractals.

We can also consider negative values of :
* For between -2 and -1 the logistic sequence also features chaotic behavior.
* With between -1 and 1 -  and for ₀ between 1/ and 1-1/, the population will approach permanent oscillations between two values, as with the case of between 3 and 1 + , and given by the same formula.

=The Emergence of Chaos

=

When the parameter r exceeds $r_ = 3.56994...$, the logistic map exhibits chaotic behavior. Roughly speaking, chaos is a complex and irregular behavior that occurs despite the fact that the difference equation describing the logistic map has no probabilistic ambiguity and the next state is completely and uniquely determined. The range of $r > r_$ of the logistic map is called the chaotic region.

One of the properties of chaos is its unpredictability, symbolized by the term butterfly effect. This is due to the property of chaos that a slight difference in the initial state can lead to a huge difference in the later state. In terms of a discrete dynamical system, if we have two initial values $x_0$ and $\hat_0$
No matter how close they are, once time n has progressed to a certain extent, each destination $x_n$ and $\hat_n$ can vary significantly. For example, use $r = 3.95, x_0 = 0.1, \hat_0=x_0+10^$
If the orbits are calculated using two very similar initial values, 0 = 0.1000000001, the difference grows to macroscopic values that are clearly visible on the graph after about 29 iterations.

This property of chaos, called initial condition sensitivity, can be quantitatively expressed by the Lyapunov exponent. For a one-dimensional map, the Lyapunov exponent λ can be calculated as follows:

Here, log means natural logarithm. This λ is the distance between the two orbits ($x_n$ and
$\hat_n$).
A positive value of λ indicates that the system is sensitive to initial conditions, while a zero or negative value indicates that the system is not sensitive to initial conditions. When calculating λ of numerically, it can be confirmed λ remains in the range of zero or negative values in the range $r < r_$, and that λ can take positive values in the range $r > r_$.

Window, intermittent

Even beyond $r_$, the behavior does not depend simply on the parameter r. Many sophisticated mathematical structures lurk in the chaotic region for $r > r_$. In this region, chaos does not persist forever; stable periodic orbits reappear. The behavior for $r_< a \le 4$ can be broadly divided into two types:

* Stable periodic point: In this case, the Lyapunov exponent is negative.
* Aperiodic orbits: In this case, the Lyapunov exponent is positive.
The region of stable periodic points that exists for r $r_ < r \le 4$ is called a periodic window, or simply a window. If one looks at a chaotic region in an orbital diagram, the region of nonperiodic orbits looks like a cloud of countless points, with the windows being the scattered blanks surrounded by the cloud.

In each window, the cascade of period-doubling bifurcations that occurred before $r_ = 3.56994...$ occurs again. However, instead of the previous stable periodic orbits of 2 k, new stable periodic orbits such as 3×2 k and 5×2 k are generated. The first window has a period of p, and the windows from which the period-doubling cascade occurs are called windows of period p, etc.. For example, a window of period 3 exists in the region around 3.8284 < a < 3.8415, and within this region the period doublings are: 3, 6, 12, 24, ..., 3×2 k, ....

In the window region, chaos does not disappear but exists in the background. However, this chaos is unstable, so only stable periodic orbits are observed. In the window region, this potential chaos appears before the orbit is attracted from its initial state to a stable periodic orbit. Such chaos is called transient chaos. In this potential presence of chaos, windows differ from the periodic orbits that appeared before a∞.

There are an infinite number of windows in the range a∞ < a < 4. The windows have various periods, and there is a window with a period for every natural number greater than or equal to three. However, each window does not occur exactly once. The larger the value of p, the more often a window with that period occurs. A window with period 3 occurs only once, while a window with period 13 occurs 315 times. When a periodic orbit of 3 occurs in the window with period 3, the Szarkovsky order is completed, and all orbits with all periods have been seen.

If we restrict ourselves to the case where p is a prime number, the number of windows with period p is

This formula was derived for p to be a prime number, but in fact it is possible to calculate with good accuracy the number of stable p- periodic points for non-prime p as well.

The window width (the difference between a where the window begins and a where the window ends) is widest for windows with period 3 and narrows for larger periods. For example, the window width for a window with period 13 is about 3.13 × 10−6. Rough estimates suggest that about 10% of r_, 4/math> is in the window region, with the rest dominated by chaotic orbits.

The change from chaos to a window as r is increased is caused by a tangent bifurcation, where the map curve is tangent to the diagonal of y = x at the moment of bifurcation, and further parameter changes result in two fixed points where the curve and the line intersect. For a window of period p, the iterated map $f^p(x)$ exhibits tangent bifurcation, resulting in stable p-periodic orbits. The exact value of the bifurcation point for a window of period 3 is known, and if the value of this bifurcation point r is $r_3$, then $r_3 = 1 + \sqrt = 3.828427...$. The outline of this bifurcation can be understood by considering the graph of $f^3(x)$ (vertical axis $x_$, horizontal axis $x_n$).  

When we look at the behavior of $x_n$ when r = 3.8282, which is slightly smaller than the branch point $r_3$, we can see that in addition to the irregular changes, there is also a behavior that changes periodically with approximately three periods, and these occur alternately. This type of periodic behavior is called a "laminar", and the irregular behavior is called a burst, in analogy with fluids. There is no regularity in the length of the time periods of the bursts and laminars, and they change irregularly. However, when we observe the behavior at r = 3.828327, which is closer to $r_3$, the average length of the laminars is longer and the average length of the bursts is shorter than when r = 3.8282. If we further increase r, the length of the laminars becomes larger and larger, and at $r_3$ it changes to a perfect three- period.

The phenomenon in which orderly motions called laminars and disorderly motions called bursts occur intermittently is called intermittency or intermittent chaos. If we consider the parameter a decreasing from a3, this is a type of emergence of chaos. As the parameter moves away from the window, bursts become more dominant, eventually resulting in a completely chaotic state. This is also a general route to chaos, like the period doubling bifurcation route mentioned above, and routes characterized by the emergence of intermittent chaos due to tangent bifurcations are called intermittency routes.

The mechanism of intermittency can also be understood from the graph of the map. When $r$ is slightly smaller than $r_3$, there is a very small gap between the graph of $f^3(x)$ and the diagonal. This gap is called a channel, and many iterations of the map occur as the orbit passes through the narrow channel. During the passage through this channel, $x_n$ and $x_$ become very close, and the variables change almost like a periodic three orbit. This corresponds to a laminar. The orbit eventually leaves the narrow channel, but returns to the channel again as a result of the global structure of the map. While leaving the channel, it behaves chaotically. This corresponds to a burst.

Band, window finish

Looking at the entire chaotic domain, whether it is chaotic or windowed, the maximum and minimum values on the vertical axis of the orbital diagram (the upper and lower limits of the attractor) are limited to a certain range. As shown in equation (2-1), the maximum value of the logistic map is given by r/4, which is the upper limit of the attractor. The lower limit of the attractor is given by the point f(r/4) where r/4 is mapped. Ultimately, the maximum and minimum values at which xn moves on the orbital diagram depend on the parameter r

Finally, for r = 4, the orbit spans the entire range , 1

When observing an orbital map, the distribution of points has a characteristic shading. Darker areas indicate that the variable takes on values in the vicinity of the darker areas, whereas lighter areas indicate that the variable takes on values in the vicinity of the darker areas. These differences in the frequency of the points are due to the shape of the graph of the logistic map. The top of the graph, near r/4, attracts orbits with high frequency, and the area near f(r/4) that is mapped from there also becomes highly frequent, and the area near $f^2(r/4)$ that is mapped from there also becomes  highly frequent, and so on. The density distribution of points generated by the map is characterized by a quantity called an invariant measure or distribution function, and the invariant measure of the attractor is reproducible regardless of the initial value.

Looking at the beginning of the chaotic region of the orbit diagram, just beyond the accumulation point $r_ = 3.56994$ of the first period - doubling cascade, one can see that the orbit is divided into several subregions. These subregions are called bands. When there are multiple bands, the orbit moves through each band in a regular order, but the values within each band are irregular. Such chaotic orbits are called band chaos or periodic chaos, and chaos with k bands is called k -band chaos. Two-band chaos lies in the range 3.590 < r < 3.675, approximately.

As the value of r is further decreased from the left-hand end of two-band chaos, r = 3.590, the number of bands doubles, just as in the period doubling bifurcation. Let $e_p$ (for p = 1, 2, 4, ..., 2k, ...) denote the bifurcation points where p − 1 band chaos splits into p band chaos, or where p band chaos merges into p − 1 band chaos. Then, just as in the period doubling bifurcation, e p accumulates to a value as p → ∞. At this accumulation point $e_$, the number of bands becomes infinite, and the value of $e_$ is equal to the value of $r_$.

Similarly, for the bifurcation points of the period-doubling bifurcation cascade that appeared before a∞, let a p (where p = 1, 2, 4, ..., 2k, ...) denote the bifurcation points where p stable periodic orbits branch into p + 1 stable periodic orbits. In this case, if we look at the orbital diagram from $r_2$ to $e_2$, there are two reduced versions of the global orbital diagram from $r_1$ to $e_1$ in the orbital diagram from $r_2$ to $e_2$. Similarly, if we look at the orbital diagram from $r_4$ to $e_4$, there are four reduced versions of the global orbital diagram from a1 to e1 in the orbital diagram from $r_4$ to $e_4$. Similarly, there are p reduced versions of the global orbital diagram in the orbital diagram from ap to ep, and the branching structure of the logistic map has an infinite self-similar hierarchy.

A self-similar hierarchy of bifurcation structures also exists within windows. The period-doubling bifurcation cascades within a window follow the same path as the cascades of period-2k bifurcations. That is, there are an infinite number of period-doubling bifurcations within a window, after which the behavior becomes chaotic again. For example, in a window of period 3, the cascade of stable periodic orbits ends at $a_$ ≈ 3.8495. After $a_$ ≈ 3.8495, the behavior becomes band chaos of multiples of three. As a increases from $a_$, these band chaos also merge by twos, until at the end of the window there are three bands. Within such bands within a window, there are an infinite number of windows. Ultimately, the window contains a miniature version of the entire orbital diagram for 1 ≤ a ≤ 4, and within the window there exists a self-similar hierarchy of branchings.

At the end of the window, the system reverts to widespread chaos. For a period 3 window, the final 3-band chaos turns into large-area 1-band chaos at a ≈ 3.857, ending the window. However, this change is discontinuous, and the 3-band chaotic attractor suddenly changes size and turns into a 1-band. Such discontinuous changes in attractor size are called crises. Crises of this kind, which occur at the end of a window, are also called internal crises. When a crisis occurs at the end of a window, a stable periodic orbit just touches an unstable periodic point that is not visible on the orbit diagram. This creates an exit point through which the periodic orbits can escape, resulting in an internal crisis. Immediately after the internal crisis, there are periods of widespread chaos, and periods of time when the original band chaotic behavior reoccurs, resulting in a kind of intermittency similar to that observed at the beginning of a window.

When r = 4

When the parameter r = 4, the behavior becomes chaotic over the entire range , 1 At this time, the Lyapunov exponent λ is maximized, and the state is the most chaotic. The value of λ for the logistic map at r = 4 can be calculated precisely, and its value is λ = log 2. Although a strict mathematical definition of chaos has not yet been unified, it can be shown that the logistic map with r = 4 is chaotic on , 1according to one well-known definition of chaos.

The invariant measure of the density of points, ρ(x), can also be given by the exact function ρ(x) for r = 4:

Here, ρ(x) means that the fraction of points xn that fall in the infinitesimal interval ,x+dxwhen the map is iterated is given by ρ(x) dx. The frequency distribution of the logistic map with r = 4 has high density near both sides of , 1and is least dense at x = 0.5.

When r = 4, apart from chaotic orbits, there are also periodic orbits with any period. For a natural number n, the graph of $f_^n(x)$ is a curve with $2^$ peaks and $2^-1$ valleys, all of which are tangent to 0 and 1. Thus, the number of intersections between the diagonal and the graph is $2^n$, and there are $2^n$ fixed points of $f^n(x)$. The n-periodic points are always included in these $2^n$ fixed points, so any n-periodic orbit exists for $f_^n(x)$. Thus,when r = 4, there are an infinite number of periodic points on , 1 but all of these periodic points are unstable. Furthermore,the uncountably infinite set in the interval , 1 the number of periodic points is countably infinite, and so almost all orbits starting from initial values are not periodic but non-periodic. 

One of the important aspects of chaos is its dual nature: deterministic and stochastic. Dynamical systems are deterministic processes, but when the range of variables is appropriately coarse-grained, they become indistinguishable from stochastic processes. In the case of the logistic map with r = 4, the outcome of every coin toss can be described by the trajectory of the logistic map. This can be elaborated as follows.

Assume that a coin is tossed with a probability of 1/2 landing on heads or tails, and the coin is tossed repeatedly. If heads is 0 and tails is 1, then the result of heads, tails, heads, tails, etc. will be a symbol string such as 01001.... On the other hand, for the trajectory $x_0, x_1, x_2, ...$ of the logistic map, values less than x = 0.5 are converted to 0 and values greater than x = 0.5 are converted to 1, and the trajectory is replaced with a symbol string consisting of 0s and 1s. For example, if the initial value is $x_0 = 0.2$, then $x_1 = 0.64$, $x_2 = 0.9216$, $x_3 = 0.28901$, ..., so the trajectory will be the symbol string 0110.... Let $S_C$ be the symbol string resulting from the former coin toss, and $S_L$ be the symbol string resulting from the latter logistic map. The symbols in the symbol string $S_C$ were determined by random coin tossing, so any number sequence patterns are possible. So, whatever the string $S_L$ of the logistic map, there is an identical one in $S_C$. And, what is "remarkable" is that the converse is also true: whatever the string of $S_C$, it can be realized by a logistic map trajectory $S_L$ by choosing the appropriate initial values. That is, for any $S_C$, there exists a unique point $x_0$ in , 1such that $S_C = S_L$.

When r > 4

When the parameter r exceeds 4, the vertex r /4 of the logistic map graph exceeds 1. To the extent that the graph penetrates 1, trajectories can escape , 1

The bifurcation at r = 4 is also a type of crisis, specifically a boundary crisis. In this case, the attractor at , 1becomes unstable and collapses, and since there is no attractor outside it, the trajectory diverges to infinity.

On the other hand, there are orbits that remain in , 1even if r > 4. Easy-to-understand examples are fixed points and periodic points in , 1 which remain in , 1 However, there are also orbits that remain in , 1other than fixed points and periodic points.

Let $A_0$ be the interval of x such that f  (x) > 1. As mentioned above,once a variable $x_n$ enters $A_0$, it diverges to minus infinity. There is also $r_n$ x in , 1that maps to $A_0$ after one application of the map. This interval of x is divided into two, which are collectively called $A_1$. Similarly, there are four intervals that map to $A_1$ after one application of the map, which are collectively called $A_2$. Similarly,there are 2n intervals $A_n$ that reach $A_0$ after n iterations. Therefore, the interval $\Lambda$ obtained by removing $A_n$ from , 1an infinite number of times as follows is a collection of orbits that remain in I.

The process of removing $A_n$ from , 1is similar to the construction of the Cantor set mentioned above, and in fact Λ exists in , 1as a Cantor set (a closed, completely disconnected, and complete subset of , 1. Furthermore, on $\Lambda$, the logistic map $f_$ is chaotic.

When r < 0

Since the logistic map has been often studied as an ecological model, the case where the parameter r is negative has rarely been discussed. As a decreases from 0, when −1 < r < 0, the map asymptotically approaches a stable fixed point of xf = 0, but when a exceeds −1, it bifurcates into two periodic points, and as in the case of positive values, it passes through a period doubling bifurcation and reaches chaos. Finally, when a falls below −2, the map diverges to plus infinity.

Exact solutions for special cases

For a logistic map with a specific parameter $a$, an exact solution that explicitly includes the time $n$ and the initial value $x_0$ has been obtained as follows.

When r = 4

When r = 2

When r = −2

Considering the three exact solutions above, all of them are

Chaos and the logistic map

The relative simplicity of the logistic map makes it a widely used point of entry into a consideration of the concept of chaos. A rough description of chaos is that chaotic systems exhibits: (see Chaotic dynamics)
* Great sensitivity on initial conditions: i.e. for a small or infinitesimal variation in the initial conditions you may have a large finite effect.
* Topologically transitive: i.e. the system tends to occupy all available states in a similar sense to fluid mixing.
* The system exhibits dense periodic orbits

These are properties of the logistic map for most values of between about 3.57 and 4 (as noted above). A common source of such sensitivity to initial conditions is that the map represents a repeated folding and stretching of the space on which it is defined. In the case of the logistic map, the quadratic difference equation describing it may be thought of as a stretching-and-folding operation on the interval .

The following figure illustrates the stretching and folding over a sequence of iterates of the map. Figure (a), left, shows a two-dimensional Poincaré plot of the logistic map's state space for , and clearly shows the quadratic curve of the difference equation (). However, we can embed the same sequence in a three-dimensional state space, in order to investigate the deeper structure of the map. Figure (b) demonstrates this, showing how initially nearby points begin to diverge, particularly in those regions of corresponding to the steeper sections of the plot.

This stretching-and-folding does not just produce a gradual divergence of the sequences of iterates, but an exponential divergence (see Lyapunov exponents), evidenced also by the complexity and unpredictability of the chaotic logistic map. In fact, exponential divergence of sequences of iterates explains the connection between chaos and unpredictability: a small error in the supposed initial state of the system will tend to correspond to a large error later in its evolution. Hence, predictions about future states become progressively (indeed, exponentially) worse when there are even very small errors in our knowledge of the initial state. This quality of unpredictability and apparent randomness led the logistic map equation to be used as a pseudo-random number generator in early computers.

At = 2, the function $rx(1-x)$ intersects $y = x$ precisely at the maximum point, so convergence to the equilibrium point is on the order of $\delta^$. Consequently, the equilibrium point is called "superstable". Its Lyapunov exponent is $-\infty$. A similar argument shows that there is a superstable $r$ value within each interval where the dynamical system has a stable cycle. This can be seen in the Lyapunov exponent plot as sharp dips.

Since the map is confined to an interval on the real number line, its dimension is less than or equal to unity. Numerical estimates yield a correlation dimension of ( Grassberger, 1983), a Hausdorff dimension of about 0.538 ( Grassberger 1981), and an information dimension of approximately 0.5170976 ( Grassberger 1983) for (onset of chaos). Note: It can be shown that the correlation dimension is certainly between 0.4926 and 0.5024.

It is often possible, however, to make precise and accurate statements about the ''likelihood'' of a future state in a chaotic system. If a (possibly chaotic) dynamical system has an attractor, then there exists a probability measure that gives the long-run proportion of time spent by the system in the various regions of the attractor. In the case of the logistic map with parameter and an initial state in , the attractor is also the interval and the probability measure corresponds to the beta distribution with parameters and . Specifically, the invariant measure is

$\frac.$

Unpredictability is not randomness, but in some circumstances looks very much like it. Hence, and fortunately, even if we know very little about the initial state of the logistic map (or some other chaotic system), we can still say something about the distribution of states arbitrarily far into the future, and use this knowledge to inform decisions based on the state of the system.

Graphical representation

The bifurcation diagram for the logistic map can be visualized with the following Python code:

import numpy as np
import matplotlib.pyplot as plt

interval = (2.8, 4) # start, end
accuracy = 0.0001
reps = 600 # number of repetitions
numtoplot = 200
lims = np.zeros(reps)

fig, biax = plt.subplots()
fig.set_size_inches(16, 9)

lims = np.random.rand()
for r in np.arange(interval interval accuracy):
for i in range(reps - 1):
lims + 1= r * lims * (1 - lims

biax.plot( * numtoplot, lims eps - numtoplot : "b.", markersize=0.02)

biax.set(xlabel="r", ylabel="x", title="logistic map")
plt.show()

Special cases of the map

Upper bound when

Although exact solutions to the recurrence relation are only available in a small number of cases, a closed-form upper bound on the logistic map is known when . There are two aspects of the behavior of the logistic map that should be captured by an upper bound in this regime: the asymptotic geometric decay with constant , and the fast initial decay when is close to 1, driven by the term in the recurrence relation. The following bound captures both of these effects:

$\forall n \in \ \quad \text \quad x_0, r \in$, 1 \quad x_n \le \frac.

Solution when

The special case of can in fact be solved exactly, as can the case with ; however, the general case can only be predicted statistically.
The solution when is:

$x_=\sin^\left(2^ \theta \pi\right),$

where the initial condition parameter is given by

$\theta = \tfrac\sin^\left(\sqrt\right).$

For rational , after a finite number of iterations maps into a periodic sequence. But almost all are irrational, and, for irrational , never repeats itself – it is non-periodic. This solution equation clearly demonstrates the two key features of chaos – stretching and folding: the factor shows the exponential growth of stretching, which results in sensitive dependence on initial conditions, while the squared sine function keeps folded within the range .

For an equivalent solution in terms of complex numbers instead of trigonometric functions is

$x_n=\frac$

where is either of the complex numbers

$\alpha = 1 - 2x_0 \pm \sqrt$

with modulus equal to 1. Just as the squared sine function in the trigonometric solution leads to neither shrinkage nor expansion of the set of points visited, in the latter solution this effect is accomplished by the unit modulus of .

By contrast, the solution when is

$x_n = \tfrac - \tfrac\left(1-2x_0\right)^$

for . Since for any value of other than the unstable fixed point 0, the term goes to 0 as goes to infinity, so goes to the stable fixed point .

Finding cycles of any length when

For the case, from almost all initial conditions the iterate sequence is chaotic. Nevertheless, there exist an infinite number of initial conditions that lead to cycles, and indeed there exist cycles of length for ''all'' integers . We can exploit the relationship of the logistic map to the dyadic transformation (also known as the ''bit-shift map'') to find cycles of any length. If follows the logistic map and follows the ''dyadic transformation''

$y_=\begin2y_n & 0 \le y_n < \tfrac12 \\2y_n -1 & \tfrac12 \le y_n < 1, \end$

then the two are related by a homeomorphism

$x_=\sin^\left(2 \pi y_\right).$

The reason that the dyadic transformation is also called the bit-shift map is that when is written in binary notation, the map moves the binary point one place to the right (and if the bit to the left of the binary point has become a "1", this "1" is changed to a "0"). A cycle of length 3, for example, occurs if an iterate has a 3-bit repeating sequence in its binary expansion (which is not also a one-bit repeating sequence): 001, 010, 100, 110, 101, or 011. The iterate 001001001... maps into 010010010..., which maps into 100100100..., which in turn maps into the original 001001001...; so this is a 3-cycle of the bit shift map. And the other three binary-expansion repeating sequences give the 3-cycle 110110110... → 101101101... → 011011011... → 110110110.... Either of these 3-cycles can be converted to fraction form: for example, the first-given 3-cycle can be written as → → → . Using the above translation from the bit-shift map to the $r = 4$ logistic map gives the corresponding logistic cycle 0.611260467... → 0.950484434... → 0.188255099... → 0.611260467.... We could similarly translate the other bit-shift 3-cycle into its corresponding logistic cycle. Likewise, cycles of any length can be found in the bit-shift map and then translated into the corresponding logistic cycles.

However, since almost all numbers in are irrational, almost all initial conditions of the bit-shift map lead to the non-periodicity of chaos. This is one way to see that the logistic map is chaotic for almost all initial conditions.

The number of cycles of (minimal) length for the logistic map with (tent map with ) is a known integer sequence : 2, 1, 2, 3, 6, 9, 18, 30, 56, 99, 186, 335, 630, 1161.... This tells us that the logistic map with has 2 fixed points, 1 cycle of length 2, 2 cycles of length 3 and so on. This sequence takes a particularly simple form for prime : . For example: 2 ⋅  = 630 is the number of cycles of length 13. Since this case of the logistic map is chaotic for almost all initial conditions, all of these finite-length cycles are unstable.

Universality

A class of mappings that exhibit homogeneous behavior

The bifurcation pattern shown above for the logistic map is not limited to the logistic map . It appears in a number of maps that satisfy certain conditions . The following dynamical system using sine functions is one example :

Here, the domain is 0 ≤ b ≤ 1 and 0 ≤ x ≤ 1 . The sine map ( 4-1 ) exhibits qualitatively identical behavior to the logistic map ( 1-2 ) : like the logistic map, it also becomes chaotic via a period doubling route as the parameter b increases, and moreover, like the logistic map, it also exhibits a window in the chaotic region .

Both the logistic map and the sine map are one-dimensional maps that map the interval , 1to , 1and satisfy the following property, called unimodal .

$f(0)=f(1)= 0$.
The map is differentiable and there exists a unique critical point c in , 1such that $f'( c ) = 0$.
In general, if a one-dimensional map with one parameter and one variable is unimodal and the vertex can be approximated by a second-order polynomial, then, regardless of the specific form of the map, an infinite period-doubling cascade of bifurcations will occur for the parameter range 3 ≤ r ≤ 3.56994... , and the ratio δ defined by equation ( 3-13 ) is equal to the Feigenbaum constant, 4.669... .

The pattern of stable periodic orbits that emerge from the logistic map is also universal . For a unimodal map, $x_ = cf ( x_n )$ , with parameter c, stable periodic orbits with various periods continue to emerge in a parameter interval where the two fixed points are unstable, and the pattern of their emergence (the number of stable periodic orbits with a certain period and the order of their appearance) is known to be common . In other words, for this type of map, the sequence of stable periodic orbits is the same regardless of the specific form of the map . For the logistic map, the parameter interval is 3 < a < 4, but for the sine map ( 4-1 ), the parameter interval for the common sequence of stable periodic orbits is 0.71... < b < 1 . This universal sequence of stable periodic orbits is called the U sequence .

In addition, the logistic map has the property that its Schwarzian derivative is always negative on the interval , 1. The Schwarzian derivative of a map f (of class C3 ) is 

In fact, when we calculate the Schwarzian derivative of the logistic map, we get

where the Schwarzian derivative is negative regardless of the values of a and x . It is known that if a one-dimensional mapping from , 1to , 1is unimodal and has a negative Schwarzian derivative, then there is at most one stable periodic orbit .

Topological conjugate mapping

Let the symbol ∘ denote the composition of maps . In general, for  a topological space X, Y, two maps f  : X → X and g  : Y → Y are composed by a homeomorphism h : X → Y.

f and g are said to be phase conjugates if they satisfy the relation . The concept of phase conjugation plays an important role in the study of dynamical systems . Phase conjugate f and g exhibit essentially identical behavior, and if the behavior of f is periodic, then g is also periodic, and if the behavior of f is chaotic, then g is also chaotic .

In particular, if a homeomorphism h is linear, then f and g are said to be linearly conjugate . Every quadratic function is linearly conjugate with every other quadratic function . Hence,

are linearly conjugates of the logistic map for any parameter a . Equations ( 4-6 ) and ( 4-7 ) are also called logistic maps . In particular, the form ( 4-7 ) is suitable for time-consuming numerical calculations, since it requires less computational effort .

Moreover, the logistic map $f_$ for $r = 4$ is topologically conjugate to the following tent map T  ( x ) and Bernoulli shift map B  ( x ) .

These phase conjugate relations can be used to prove that the logistic map $f_$ is strictly chaotic and to derive the exact solution ( 3-19 ) of $f_$ .

Alternatively, introducing the concept of symbolic dynamical systems, consider the following shift map σ defined on the symbolic string space consisting of strings of 0s and 1s as introduced above :

Here, $s_i$ is 0 or 1. On the set $\Lambda$ introduced in equation ( 3-18 ), the logistic map $f_$ is topologically conjugate to the shift map, so we can use this to derive that $f_$ on $\Lambda$ is chaotic .

Period-doubling route to chaos

In the logistic map, we have a function $f_r (x) = rx(1-x)$, and we want to study what happens when we iterate the map many times. The map might fall into a fixed point, a fixed cycle, or chaos. When the map falls into a stable fixed cycle of length $n$, we would find that the graph of $f_r^n$ and the graph of $x\mapsto x$ intersects at $n$ points, and the slope of the graph of $f_r^n$ is bounded in $(-1, +1)$ at those intersections.

For example, when $r=3.0$, we have a single intersection, with slope bounded in $(-1, +1)$, indicating that it is a stable single fixed point.

As $r$ increases to beyond $r=3.0$, the intersection point splits to two, which is a period doubling. For example, when $r=3.4$, there are three intersection points, with the middle one unstable, and the two others stable.

As $r$ approaches $r = 3.45$, another period-doubling occurs in the same way. The period-doublings occur more and more frequently, until at a certain $r\approx 3.56994567$, the period doublings become infinite, and the map becomes chaotic. This is the period-doubling route to chaos.

Scaling limit

Looking at the images, one can notice that at the point of chaos $r^* = 3.5699\cdots$, the curve of $f^_$ looks like a fractal. Furthermore, as we repeat the period-doublings$f^_, f^_, f^_, f^_, f^_, \dots$, the graphs seem to resemble each other, except that they are shrunken towards the middle, and rotated by 180 degrees.

This suggests to us a scaling limit: if we repeatedly double the function, then scale it up by $\alpha$ for a certain constant $\alpha$:$f(x) \mapsto - \alpha f( f(-x/\alpha ) )$then at the limit, we would end up with a function $g$ that satisfies $g(x) = - \alpha g( g(-x/\alpha ) )$. This is a Feigenbaum function, which appears in most period-doubling routes to chaos (thus it is an instance of universality). Further, as the period-doubling intervals become shorter and shorter, the ratio between two period-doubling intervals converges to a limit, the first Feigenbaum constant $\delta = 4.6692016\cdots$.
The constant $\alpha$ can be numerically found by trying many possible values. For the wrong values, the map does not converge to a limit, but when it is $\alpha = 2.5029\dots$, it converges. This is the second Feigenbaum constant.

Chaotic regime

In the chaotic regime, $f^\infty_r$, the limit of the iterates of the map, becomes chaotic dark bands interspersed with non-chaotic bright bands.

Other scaling limits

When $r$ approaches $r \approx 3.8494344$, we have another period-doubling approach to chaos, but this time with periods 3, 6, 12, ... This again has the same Feigenbaum constants $\delta, \alpha$. The limit of $f(x) \mapsto - \alpha f( f(-x/\alpha ) )$ is also the same Feigenbaum function. This is an example of universality.

We can also consider period-tripling route to chaos by picking a sequence of $r_1, r_2, \dots$ such that $r_n$ is the lowest value in the period-$3^n$ window of the bifurcation diagram. For example, we have $r_1 = 3.8284, r_2 = 3.85361, \dots$, with the limit $r_\infty = 3.854 077 963\dots$. This has a different pair of Feigenbaum constants $\delta= 55.26\dots, \alpha = 9.277\dots$. And $f^\infty_r$converges to the fixed point to $f(x) \mapsto - \alpha f(f( f(-x/\alpha ) ))$As another example, period-4-pling has a pair of Feigenbaum constants distinct from that of period-doubling, even though period-4-pling is reached by two period-doublings. In detail, define $r_1, r_2, \dots$ such that $r_n$ is the lowest value in the period-$4^n$ window of the bifurcation diagram. Then we have $r_1 =3.960102, r_2 = 3.9615554, \dots$, with the limit $r_\infty = 3.96155658717\dots$. This has a different pair of Feigenbaum constants $\delta= 981.6\dots, \alpha = 38.82\dots$.

In general, each period-multiplying route to chaos has its own pair of Feigenbaum constants. In fact, there are typically more than one. For example, for period-7-pling, there are at least 9 different pairs of Feigenbaum constants.

Generally, $3\delta \approx 2\alpha^2$, and the relation becomes exact as both numbers increase to infinity: $\lim \delta/\alpha^2 = 2/3$.

Feigenbaum universality of 1-D maps

Universality of one-dimensional maps with parabolic maxima and Feigenbaum constants $\delta=4.669201...$, $\alpha=2.502907...$.

The gradual increase of $G$ at interval $[0, \infty)$ changes dynamics from regular to chaotic one with qualitatively the same bifurcation diagram as those for logistic map.

Renormalization estimate

The Feigenbaum constants can be estimated by a renormalization argument. (Section 10.7,).

By universality, we can use another family of functions that also undergoes repeated period-doubling on its route to chaos, and even though it is not exactly the logistic map, it would still yield the same Feigenbaum constants.

Define the family $f_r(x) = -(1+r)x + x^2$The family has an equilibrium point at zero, and as $r$ increases, it undergoes period-doubling bifurcation at $r = r_0, r_1, r_2, ...$.

The first bifurcation occurs at $r = r_0 = 0$. After the period-doubling bifurcation, we can solve for the period-2 stable orbit by $f_r(p) = q, f_r(q) = p$, which yields $\begin p = \frac 12 (r + \sqrt) \\ q = \frac 12 (r - \sqrt) \end$At some point $r = r_1$, the period-2 stable orbit undergoes period-doubling bifurcation again, yielding a period-4 stable orbit. In order to find out what the stable orbit is like, we "zoom in" around the region of $x = p$, using the affine transform $T(x) = x/c + p$. Now, by routine algebra, we have$(T^\circ f_r^2 \circ T)(x) = -(1+S(r)) x + x^2 + O(x^3)$where $S(r) = r^2 + 4r - 2, c = r^2 + 4r - 3\sqrt$. At approximately $S(r) = 0$, the second bifurcation occurs, thus $S(r_1) \approx 0$.

By self-similarity, the third bifurcation when $S(r) \approx r_1$, and so on. Thus we have $r_n \approx S(r_)$, or $r_ \approx \sqrt-2$. Iterating this map, we find $r_\infty = \lim_n r_n \approx \lim_n S^(0) = \frac 12(\sqrt-3)$, and $\lim_n \frac \approx S'(r_\infty) \approx 1 + \sqrt$.

Thus, we have the estimates $\delta \approx 1+\sqrt = 5.12...$, and $\alpha \approx r_\infty^2 +4r_\infty- 3 \sqrt \approx -2.24...$. These are within 10% of the true values.

Relation to logistic ordinary differential equation

The logistic map exhibits numerous characteristics of both periodic and chaotic solutions, whereas the logistic ordinary differential equation (ODE) exhibits regular solutions, commonly referred to as the S-shaped sigmoid function. The logistic map can be seen as the discrete counterpart of the logistic ODE, and their correlation has been extensively discussed in literature.

The logistic map as a model of biological populations

Discrete population model

While Lorenz used the logistic map in 1964, it gained widespread popularity from the research of British mathematical biologist Robert May and became widely known as a formula for considering changes in populations of organisms. In such a logistic map for organism populations, the variable $x_n$ represents the number of organisms living in a certain environment (more technically, the population size). Furthermore, it is assumed that no organisms leave the environment and no external organisms enter the environment (or that there is no substantial impact even if there is immigration), and the mathematical model for considering the increase or decrease in population in such a situation is the logistic map in mathematical biology .

There are two types of mathematical models for the growth of populations of organisms: discrete-time models using difference equations and continuous-time models using differential equations . For example, in the case of a type of insect that dies soon after laying eggs, the population of the insect is counted for each generation, i.e., the number of individuals in the first generation, the number of individuals in the second generation, and so on . Such examples fit the former discrete-time model . On the other hand, when the generations are continuously overlapping, it is compatible with the continuous-time model . The logistic map corresponds to such a discrete or generation-separated population model .

Let N denote the number of individuals of a single species in an environment . The simplest model for population growth is one in which the population continues to grow at a constant rate relative to the number of individuals. This type of population growth model is called the Malthusian model, and can be expressed as follows :

Here, N n is the number of individuals in the nth generation, and α is the population growth rate, a positive constant . However, in model ( 5-1 ), the population continues to grow indefinitely, making it an unrealistic model for most real-world phenomena . Since there is a limit to the number of individuals that an environment can support, it seems natural that the growth rate α decreases as the population N n increases . This change in growth rate due to changes in population density is called the density effect . The following difference equation is the simplest improvement model that reflects the density effect in model ( 5-1 ).

Here, a is the maximum growth rate possible in the environment, and b is the strength of the influence of density effects . Model ( 5-2 ) assumes that the growth rate declines simply in proportion to the number of individuals . Let N n in equation ( 5-2 ) be

After performing the variable transformation, the following logistic map is derived :

When using equation ( 5-2 ) or equation ( 5-4 ) as the population size of an organism, if Nn or xn becomes negative, it becomes meaningless as a population size . To prevent this, the condition 0 ≤ x0 ≤ 1 for the initial value x0 and the condition 0 ≤ r ≤ 4 for the parameter a are required .

Alternatively, we can assume a maximum population size K that the environment can support, and use this to

The logistic map can be derived by considering a difference equation that incorporates density effects in the form $x_n = N_n / K$ , where the variable $x_n$ represents the ratio of the number of individuals $N_n$ to the maximum number of individuals K .

Discretization of the logistic equation

The logistic map can also be derived from the discretization of the logistic equation for continuous-time population models . The name of the logistic map comes from Robert May's introduction of the logistic map from the discretization of the logistic equation. The logistic equation is an ordinary differential equation that describes the time evolution of a population as follows :

Here, N is the number or population density of an organism, t is continuous time, and K and r are parameters. K is the carrying capacity, and r is the intrinsic rate of natural increase, which is usually positive . The left-hand side of this equation
dN/dt
denotes the rate of change of the population size at time t .

The logistic equation ( 5-6 ) appears similar to the logistic map ( 5-4 ), but the behavior of the solutions is quite different from that of the logistic map . As long as the initial value N 0 is positive, the population size N of the logistic equation always converges monotonically to K .

The logistic map can be derived by applying the Euler method, which is a method for numerically solving first-order ordinary differential equations, to this logistic equation . [ Note 2 ] The Euler method uses a time interval (time step size) Δt to approximate the growth rate dN/dt
is approximated as follows :

This approximation leads to the following logistic map :

where $x_n$ and a in this equation are related to the original parameters, variables, and time step size as follows :

If Δt is small enough, equation ( 5-8 ) serves as a valid approximation to the original equation ( 5-6 ), and coincides with the solution of the original equation as Δt → 0 . On the other hand, as Δt becomes large, the solution deviates from the original solution . Furthermore, due to the relationship in equation ( 5-10 ), increasing Δt is equivalent to increasing the parameter a . Thus, increasing Δt not only increases the error from the original equation but also produces chaotic behavior in the solution .

Positioning

As described above, in biological population dynamics, the logistic map is one of the models of discrete growth processes. However, unlike the laws of physics, the logistic map as a model of biological population size is not derived from direct experimental results or universally valid principles . Although there is some rationality in the way it is derived, it is essentially a "model" thought up in one's mind . May, who made the logistic map famous, did not claim that the model he was discussing accurately represented the increase and decrease in population size . Historically, continuous-time models based on differential equations have been widely used in the study of biological population dynamics, and the application of these continuous-time models has deepened our understanding of biological population dynamics . As a discrete-time population model that takes into account density effects, the Ricker model, in which the population size is not negative, is more realistic .

Generally speaking, mathematical models can provide important qualitative information about population dynamics, but their results should not be taken too seriously without experimental support . Even if the conclusions of mathematical models deviate from those of biological studies, mathematical modeling is still useful because it can provide a useful control. Biological issues may be raised by reviewing the model construction process and settings, or the biological knowledge and assumptions that the model is based on. Although the logistic map is too simple to be realistic as a population model, its results suggest that a variety of population fluctuations may occur due to the dynamics inherent in the population itself, regardless of random influences from the environment.

Applications

Coupled map system

The degree of freedom or dimension of a one-variable logistic map as a system is one . On the other hand, in the real natural world, it is thought that there are many chaotic systems with many degrees of freedom, not only in time but also in space . Alternatively, the synchronization phenomenon of oscillators performing chaotic motion is also a research subject . To investigate such things, there is a method of coupled maps that couples many difference equations (maps) . The logistic map is often used as a subject of coupled map model research . The reason for this is that the logistic map itself has already been well investigated as a typical model of chaos, and there is an accumulation of research on it .

There are various methods for the specific coupling in the coupled map model . Suppose a total of N maps are coupled, and the state of the i-th map at time n is represented by $x_n( i )$ . In a method called globally coupled maps, $x_( i )$ is formulated as follows :

In the current field of coupled oscillators, the simplest model is the following, in which two oscillators, x and y, are coupled by a difference in variables :

In these equations, f( x ) is the specific map to incorporate into the coupled map model, and applies here if the logistic map is used .

In equations ( 6-1 ) and ( 6-2 ), ε and D are parameters called coupling coefficients, which indicate the strength of the coupling between the maps . On the other hand, when the logistic map is incorporated into a coupled map model, the parameter a of the logistic map indicates the strength of the nonlinearity of the model . By changing the value of a and the value of ε or D, various phenomena appear in the coupled map system of logistic maps. For example, in model ( 6-2 ), when D is increased to a value Dc or more, x and y oscillate chaotically while synchronously . Even below Dc, not only do chaotic oscillations occur in a continuous manner . When D is in a certain range, x and y oscillate with two periods even though r = 4 . When a = 3.8, behavior in which synchronous and asynchronous states alternate continuously is also observed .

In a study of the application of the logistic map to a globally coupled map with a large degree of freedom ( 6-1 ), a phenomenon called chaotic itinerancy was found . This is a phenomenon in which the orbit traverses a region in phase space that is said to be the remains of an attractor, repeating the cycle from an orderly state in which several clusters oscillate together to a disordered state, then to another cluster state, then back to the disordered state again, and so on .

Pseudorandom number generator

In the fields of computer simulation and information security, the creation of pseudorandom numbers using a computer is an important technique, and one of the methods for generating pseudorandom numbers is the use of chaos. Although a pseudorandom number generator based on chaos with sufficient performance has not yet been realized, several methods have been proposed. Several researchers have also investigated the possibility of creating a pseudorandom number generator based on chaos for the logistic map.

Parameter r = 4 is often used for pseudorandom number generation using the logistic map. Historically, as described below, in 1947, shortly after the birth of electronic computers, Stanisław Ulam and John von Neumann also pointed out the possibility of a pseudorandom number generator using the logistic map with r = 4. However, the distribution of points for the logistic map $f_$ is as shown in equation ( 3-17 ), and the numbers that are generated are biased toward 0 and 1. Therefore, some processing is required to obtain unbiased uniform random numbers. Methods for doing so include:

A method for converting the obtained values to a uniform distribution using the tent map ( 4-8 ).
The resulting number is converted to either 0 or 1 using a threshold, as in the coin tossing analogy above, and this process is repeated to obtain a uniformly random bit stringm
In addition, the sequences $x_n$ and $x_n +1$ obtained by the logistic map are strongly correlated, which makes it problematic for pseudorandom sequences. One way to solve this is to generate the sequence $x_0, x_1, x_2, ...$ for each iteration of the map, rather than generating the sequence $x_0, x_, x_ ,...$ for some number of iterations τ > 1 For example, it is said that good pseudorandom numbers can be obtained for method 1 with τ > 10 or τ > 13, and for method 2 with τ > 16.

A common problem with digitally calculating chaos using a computer is that, because a computer has a finite calculation precision, it is in principle impossible to obtain a truly aperiodic sequence, which is the nature of chaos, and instead outputs a finite periodic sequence. Even if aperiodic sequences cannot be obtained in principle, sequences with as long a period as possible are desirable for generating pseudorandom numbers. However, when the periodicity of the sequence actually output by the logistic map $f_$ in single-precision floating-point calculations was investigated, it was reported that the period of the sequence actually output is much smaller than the maximum period possible from the number of bits allocated, and from this point of view, it has been pointed out that pseudorandom number generation by the logistic map is inferior to existing pseudorandom number generators such as the Mersenne Twister. In addition, with the logistic map, $f_$ there is a risk that the value will fall to the fixed point 0 during the calculation and remain constant. On the other hand, the logistic map always takes values in the open interval (0, 1), so it can be calculated without problems not only with floating point but also with fixed point, and can enjoy the advantages of fixed point arithmetic. It has been pointed out that fixed point has a longer period than floating point for the same number of bits, and that unintended convergence to 0 can be eliminated.

Extension to complex numbers

Dynamical systems defined by complex analytic functions are also of interest.LP An example is the dynamical system defined by the quadratic function:

where the parameter c and the variable z are complex numbers. This map is essentially the same as the logistic map (1–2). As mentioned above, the map (6–3) is topologically conjugate to the logistic map (1–2) through a linear function.

When the iteration of the map (6–3) is calculated with a fixed parameter c and varying the initial value $z_0$, a set of $z_0$ such that $z_n$ does not diverge to infinity as n → ∞ is called a filled Julia set. Furthermore, the boundary of a filled Julia set is called a Julia set. When the iteration of the map (6–3) is calculated with a fixed initial value $z_0 = 0$ and varying the parameter , a set of such that does not diverge to infinity is called a Mandelbrot set. The Julia sets and Mandelbrot sets of the map (6–3) generate fractal figures that are described as "mystical looking" and "extremely mysterious".

In particular, in the Mandelbrot set, each disk in the diagram corresponds to a region of asymptotically stable periodic orbits of a certain period. By juxtaposing the logistic map orbit diagram with the Mandelbrot set diagram, it is possible to see that the asymptotically stable fixed points, period doubling bifurcations, and period-three windows of the logistic map orbit diagram correspond on the real axis to the Mandelbrot set diagram.

When there is a time delay

If we interpret the logistic map as a model of the population of each generation of organisms, it is possible that the population of the next generation will affect not only the population of the current generation, but also the population of the generation before that. An example of such a case is

where the number of individuals in the previous generation, $x_$, is included in the equation as a negative density effect . If $x_ = y_n$, then equation ( 6-4 ) can be replaced by the following two-variable difference equation .

This dynamical system is used to study bifurcation of quasi-periodic attractors and is called the delayed logistic map . The delayed logistic map exhibits a Neimark–Sakher bifurcation at r = 2, where the asymptotically stable fixed point becomes unstable and an asymptotically stable invariant curve forms around the unstable fixed point .

Research history

Before Chaos was named

Before the iteration of maps became relevant to dynamical systems, mathematicians Gaston Julia and Pierre Fatou studied the iteration of complex functions. Julia and Fatou's work was broad, focusing on analytic functions. In particular, they studied the behavior of the following complex quadratic function, also shown in equation (6–3), in the 1920s.

Julia and Fatu also recognized chaotic behavior in Julia sets, but because there was no computer graphics at the time, no one followed suit and their research stalled. Research on complex dynamical systems then declined until the late 1970s, and it was not until the appearance of Benoit Mandelbrot and others that the rich dynamical behavior exhibited by maps on the complex plane was noticed.

In 1947, mathematicians Stanislaw Ulam and John von Neumann wrote a short paper entitled "On combination of stochastic and deterministic processes" in which they

They pointed out that pseudorandom numbers can be generated by the repeated composition of quadratic functions such as. In modern terms, this equation corresponds to the logistic map with = 4. At that time, the word "chaos" had not yet been used, but Ulam and von Neumann were already paying attention to the generation of complex sequences using nonlinear functions. In their report, Ulam and von Neumann also clarified that the map (7–2) and the tent map are topologically conjugate, and that the invariant measure of the sequence of this map is given by equation (3–17).

There have since been some detailed investigations of quadratic maps of the form with arbitrary parameter . Between 1958 and 1963, Finnish mathematician Pekka Mylberg developed the

This line of research is essential for dynamical systems, and Mühlberg has also investigated the period-doubling branching cascades of this map, showing the existence of an accumulation point λ = 1.401155189.... Others, such as the work of the Soviet Oleksandr Sharkovsky in 1964, the French Igor Gumowski and Christian Mila in 1969, and Nicholas Metropolis in 1973, have revealed anomalous behavior of simple one-variable difference equations such as the logistic map.

Robert May's research

Later, in the early 1970s, mathematical biologist Robert May encountered the model of equation (1–2) while working on an ecological problem. May introduced equation (1–2), i.e., the logistic map, by discretizing the logistic equation in time. He mathematically analyzed the behavior of the logistic map, and published his results in 1973 and 1974. Numerical experiments were performed on the logistic map to investigate the change in its behavior depending on the parameter .

In 1976, he published a paper in ''Nature'' entitled "Simple mathematical models with very complicated dynamics". This paper was a review paper that focused on the logistic map and emphasized and drew attention to the fact that even simple nonlinear functions can produce extremely complex behaviors such as period-doubling bifurcation cascades and chaos. This paper in particular caused a great stir and was accepted by the scientific community due to May's status as a mathematical biologist, the clarity of his research results, and above all, the shocking content that a simple parabolic equation can produce surprisingly complex behavior. Through May's research, the logistic map attracted many researchers to chaos research and became such a famous mathematical model that it is said to have restarted the flow of chaos research.

After May's research

May also drew attention to the paper by using the term "chaos", which was used by Tien-Yen Li and James York in their paper "Period three implies chaos". Although some disagree, Li and York's paper is considered the first to use the word "chaos" as a mathematical term, and is credited with coining the term "chaos" to refer to deterministic, chaotic behavior. Li and York completed the paper in 1973, but when they submitted it to ''The American Mathematical Monthly'', they were told that it was too technical and that it should be significantly rewritten to make it easier to understand, and it was rejected. The paper was then left unrevised. However, the following year, in 1974, May came to give a special guest lecture at the University of Maryland where Lee and York were working, and talked about the logistic map. At the time, May did not yet understand what was happening in the chaotic domain of the logistic map, but Lee and York were also unaware of the period-doubling cascade of the logistic map. Excited by May's talk, Lee and York caught up with May after the lecture and told him about their results, which surprised May. Lee and York quickly rewrote the rejected paper, and the resubmitted paper was published in 1975.

Also, around 1975, mathematical physicist Mitchell Feigenbaum noticed a scaling law in which the branching values converged in a geometric progression when he looked at the period-doubling cascade of the logistic map, and discovered the existence of a constant, now called the Feigenbaum constant, through numerical experiments. May and George Oster had also noticed the scaling law, but they were unable to follow it in depth. Feigenbaum discovered that the same constant also appeared in the sine map shown in equation (4–1), and realized that this scaling law had a universality that went beyond the logistic map. In 1980, a rigorous proof of this result was given by Pierre Collé, Jean-Pierre Eckman, Oscar Rumford, and others. At about the same time as Feigenbaum, or later, physicists discovered the same period doubling cascade and the Feigenbaum constant in real life, and chaos, which had previously been seen as a strictly mathematical phenomenon, had a major impact on the field of physics as well.

However, there is criticism of the tendency to downplay research results from before the popularity of chaos, and to attribute many of those results to rediscoverers who used the logistic map, etc. May himself respects the existence of previous research, but positions his own achievement as not being "the first to independently discover the strange mathematical behavior of quadratic maps", but as being one of the "last researchers to emphasize their broad implications in science". Mathematician Robert Devaney states the following before explaining the logistic map in his book: