|
Attractor
In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed. In finite-dimensional systems, the evolving variable may be represented algebraically as an ''n''-dimensional vector. The attractor is a region in ''n''-dimensional space. In physical systems, the ''n'' dimensions may be, for example, two or three positional coordinates for each of one or more physical entities; in economic systems, they may be separate variables such as the inflation rate and the unemployment rate. If the evolving variable is two- or three-dimensional, the attractor of the dynamic process can be represented geometrically in two or three dimensions, (as for example in the three-dimensional case depicted to the right). An attractor can be a point, a finite set of points, a curve, a mani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strange Attractor
In the mathematics, mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed. In finite-dimensional systems, the evolving variable may be represented algebraically as an ''n''-dimensional Coordinate vector, vector. The attractor is a region in space (mathematics), ''n''-dimensional space. In Physics, physical systems, the ''n'' dimensions may be, for example, two or three positional coordinates for each of one or more physical entities; in Economics, economic systems, they may be separate variables such as the inflation rate and the unemployment rate. If the evolving variable is two- or three-dimensional, the attractor of the dynamic process can be represented Geometry, geometrically in two or three dimensions, (as for example in the three-dimensional case depicted to t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
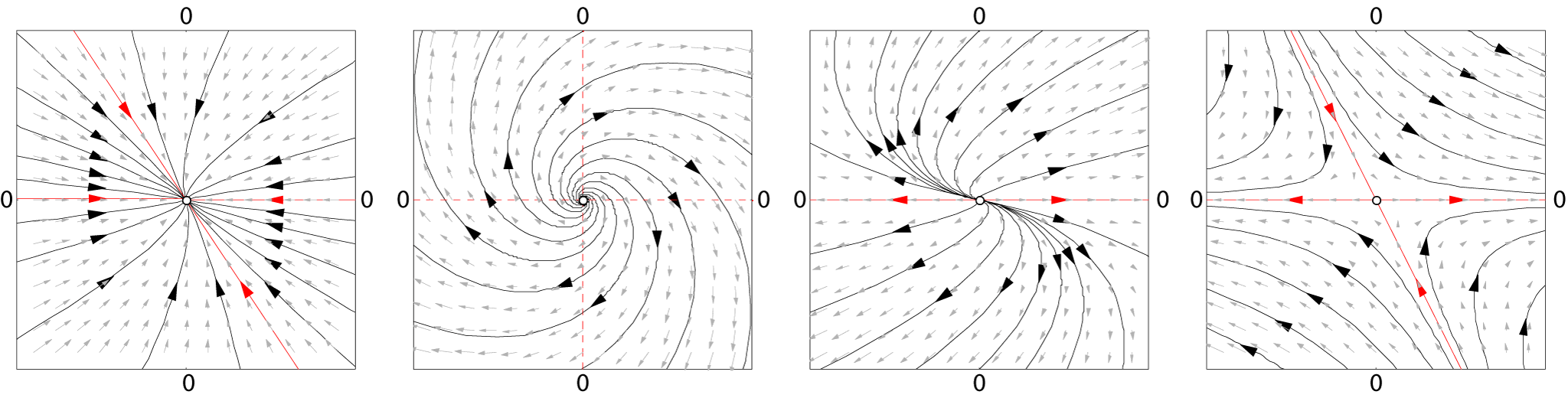
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine geometry, affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they Scaling (geometry), scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Set
In mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time. Limit sets are important because they can be used to understand the long term behavior of a dynamical system. A system that has reached its limiting set is said to be at equilibrium. Types * fixed points * periodic orbits * limit cycles * attractors In general, limits sets can be very complicated as in the case of strange attractors, but for 2-dimensional dynamical systems the Poincaré–Bendixson theorem provides a simple characterization of all nonempty, compact \omega-limit sets that contain at most finitely many fixed points as a fixed point, a periodic orbit, or a union of fixed points and homoclinic or heteroclinic orbits connecting those fixed points. Definition for iterated functions Let X be a metric space, and let f:X\rightarrow X be a continuous function. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Principles In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Saturne Revisited
Poisson may refer to: People *Siméon Denis Poisson, French mathematician * Eric Poisson, Canadian physicist Places * Poissons, a commune of Haute-Marne, France * Poisson, Saône-et-Loire, a commune of Saône-et-Loire, France Other uses * Poisson (surname), a French surname * Poisson (crater), a lunar crater named after Siméon Denis Poisson *The French word for fish See also * Adolphe-Poisson Bay, a body of water located to the southwest of Gouin Reservoir, in La Tuque, Mauricie, Quebec *Poisson distribution, a discrete probability distribution named after Siméon Denis Poisson *Poisson's equation Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with t ..., a partial differential equation named after Siméon Denis Poisson * List of things named after Siméon Denis Poisson * Poison (disa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difference Equations
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissipative System
A dissipative system is a thermodynamically open system which is operating out of, and often far from, thermodynamic equilibrium in an environment with which it exchanges energy and matter. A tornado may be thought of as a dissipative system. Dissipative systems stand in contrast to conservative systems. A dissipative structure is a dissipative system that has a dynamical regime that is in some sense in a reproducible steady state. This reproducible steady state may be reached by natural evolution of the system, by artifice, or by a combination of these two. Overview A dissipative structure is characterized by the spontaneous appearance of symmetry breaking (anisotropy) and the formation of complex, sometimes chaotic, structures where interacting particles exhibit long range correlations. Examples in everyday life include convection, turbulent flow, cyclones, hurricanes and living organisms. Less common examples include lasers, Bénard cells, droplet cluster, and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |