|
Stiff Equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proven difficult to formulate a precise definition of stiffness, but the main idea is that the equation includes some terms that can lead to rapid variation in the solution. When integrating a differential equation numerically, one would expect the requisite step size to be relatively small in a region where the solution curve displays much variation and to be relatively large where the solution curve straightens out to approach a line with slope nearly zero. For some problems this is not the case. In order for a numerical method to give a reliable solution to the differential system sometimes the step size is required to be at an unacceptably small level in a region where the solution curve is very smooth. The phenomenon is known as ''stiffness''. In some cases there may b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Servomechanism
In mechanical and control engineering, a servomechanism (also called servo system, or simply servo) is a control system for the position and its time derivatives, such as velocity, of a mechanical system. It often includes a servomotor, and uses closed-loop control to reduce steady-state error and improve dynamic response. In closed-loop control, error-sensing negative feedback is used to correct the action of the mechanism. In displacement-controlled applications, it usually includes a built-in encoder or other position feedback mechanism to ensure the output is achieving the desired effect. Following a specified motion trajectory is called servoing, where "servo" is used as a verb. The ''servo'' prefix originates from the Latin word ''servus'' meaning slave. The term correctly applies only to systems where the feedback or error-correction signals help control mechanical position, speed, attitude or any other measurable variables. For example, an automotive power win ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Function
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rational numbers; they may be taken in any field . In this case, one speaks of a rational function and a rational fraction ''over ''. The values of the variables may be taken in any field containing . Then the domain of the function is the set of the values of the variables for which the denominator is not zero, and the codomain is . The set of rational functions over a field is a field, the field of fractions of the ring of the polynomial functions over . Definitions A function f is called a rational function if it can be written in the form : f(x) = \frac where P and Q are polynomial functions of x and Q is not the zero function. The domain of f is the set of all values of x for which the denominator Q(x) is not zero. How ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicit Euler Method
In numerical analysis and scientific computing, the backward Euler method (or implicit Euler method) is one of the most basic numerical methods for the solution of ordinary differential equations. It is similar to the (standard) Euler method, but differs in that it is an implicit method. The backward Euler method has error of order one in time. Description Consider the ordinary differential equation : \frac = f(t,y) with initial value y(t_0) = y_0. Here the function f and the initial data t_0 and y_0 are known; the function y depends on the real variable t and is unknown. A numerical method produces a sequence y_0, y_1, y_2, \ldots such that y_k approximates y(t_0+kh) , where h is called the step size. The backward Euler method computes the approximations using : y_ = y_k + h f(t_, y_). This differs from the (forward) Euler method in that the forward method uses f(t_k, y_k) in place of f(t_, y_). The backward Euler method is an implicit method: the new approxi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
L-stability
Within mathematics regarding differential equations, L-stability is a special case of A-stability, a property of Runge–Kutta methods for solving ordinary differential equations. A method is L-stable if it is A-stable and \phi(z) \to 0 as z \to \infty , where \phi is the stability function of the method (the stability function of a Runge–Kutta method is a rational function and thus the limit as z \to +\infty is the same as the limit as z \to -\infty). L-stable methods are in general very good at integrating stiff equation In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proven difficult to formulate a precise ...s. References * . Numerical differential equations {{mathapplied-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trapezoidal Rule (differential Equations)
In numerical analysis and scientific computing, the trapezoidal rule is a numerical method to solve ordinary differential equations derived from the trapezoidal rule for computing integrals. The trapezoidal rule is an implicit second-order method, which can be considered as both a Runge–Kutta method and a linear multistep method. Method Suppose that we want to solve the differential equation y' = f(t,y). The trapezoidal rule is given by the formula y_ = y_n + \tfrac 1 2 h \Big( f(t_n,y_n) + f(t_,y_) \Big), where h = t_ - t_n is the step size. This is an implicit method: the value y_ appears on both sides of the equation, and to actually calculate it, we have to solve an equation which will usually be nonlinear. One possible method for solving this equation is Newton's method. We can use the Euler method to get a fairly good estimate for the solution, which can be used as the initial guess of Newton's method. Cutting short, using only the guess from Eulers method is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stability Region For Trapezoidal Method
Stability may refer to: Mathematics *Stability theory, the study of the stability of solutions to differential equations and dynamical systems **Asymptotic stability **Exponential stability **Linear stability **Lyapunov stability **Marginal stability **Orbital stability **Structural stability *Stability (probability), a property of probability distributions *Stability (learning theory), a property of machine learning algorithms *Stability, a property of Stable sorting algorithm, sorting algorithms *Numerical stability, a property of numerical algorithms which describes how errors in the input data propagate through the algorithm *Stability radius, a property of continuous polynomial functions *Stable theory, concerned with the notion of stability in model theory *Stability, a property of points in Stable point, geometric invariant theory *K-Stability, a stability condition for algebraic varieties. *Bridgeland stability conditions, a class of stability conditions on elements of a tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Method
In mathematics and computational science, the Euler method (also called the forward Euler method) is a first-order numerical analysis, numerical procedure for solving ordinary differential equations (ODEs) with a given Initial value problem, initial value. It is the most basic explicit and implicit methods, explicit method for numerical ordinary differential equations, numerical integration of ordinary differential equations and is the simplest Runge–Kutta method. The Euler method is named after Leonhard Euler, who first proposed it in his book ''Institutionum calculi integralis'' (published 1768–1770). The Euler method is a first-order method, which means that the local error (error per step) is proportional to the square of the step size, and the global error (error at a given time) is proportional to the step size. The Euler method often serves as the basis to construct more complex methods, e.g., predictor–corrector method. Geometrical description Purpose and why i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stability Region For Euler Method
Stability may refer to: Mathematics *Stability theory, the study of the stability of solutions to differential equations and dynamical systems ** Asymptotic stability **Exponential stability ** Linear stability **Lyapunov stability ** Marginal stability **Orbital stability **Structural stability *Stability (probability), a property of probability distributions * Stability (learning theory), a property of machine learning algorithms *Stability, a property of sorting algorithms *Numerical stability, a property of numerical algorithms which describes how errors in the input data propagate through the algorithm * Stability radius, a property of continuous polynomial functions *Stable theory, concerned with the notion of stability in model theory *Stability, a property of points in geometric invariant theory * K-Stability, a stability condition for algebraic varieties. * Bridgeland stability conditions, a class of stability conditions on elements of a triangulated category. * Stability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
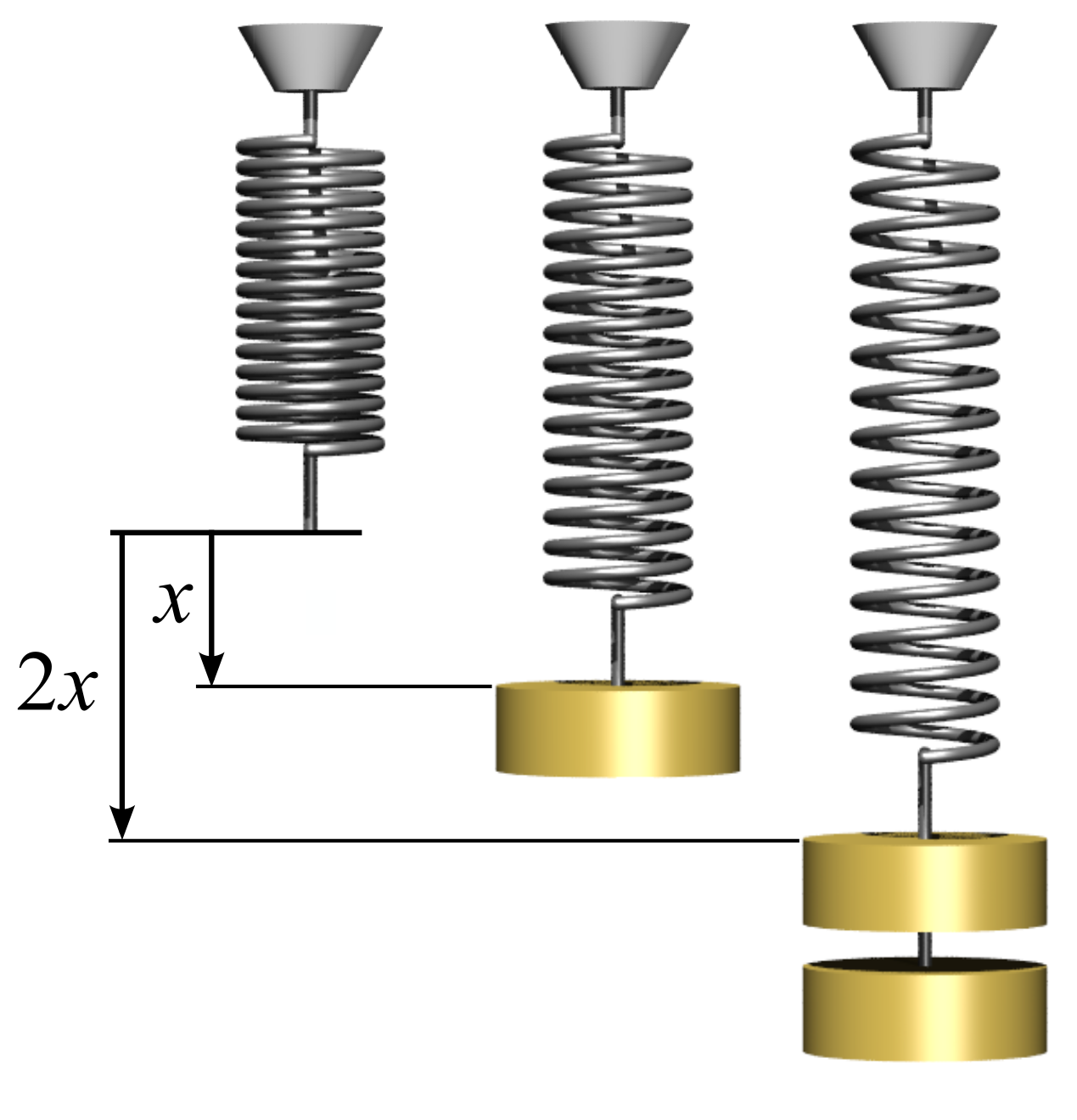
Stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force. The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is. Calculations The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (DOF) (for example, stretching or compression of a rod), the stiffness is defined as k = \frac where, * F is the force on the body * \delta is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) Stiffness is usually defined under quasi-static conditions, but sometimes under dynamic loading. In the International System of Units, stiffness is typically measured in newtons per meter (N/m). In Imperial units, stiffness is typically measured in pounds (lbs) per inch. Generally speaking, deflections (or motions) of an infinitesima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hooke's Law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |