|
Infinite Monkey Theorem
The infinite monkey theorem states that a monkey hitting keys independently and at randomness, random on a typewriter keyboard for an infinity, infinite amount of time will almost surely type any given text, including the complete works of William Shakespeare. More precisely, under the assumption of independence and randomness of each keystroke, the monkey would almost surely type every possible finite text an infinite number of times. The theorem can be generalized to state that any infinite sequence of independent events whose probabilities are uniformly bounded below by a positive number will almost surely have infinitely many occurrences. In this context, "almost surely" is a mathematical term meaning the event happens with probability 1, and the "monkey" is not an actual monkey, but a metaphor for an Abstract and concrete, abstract device that produces an endless random sequence of letters and symbols. Variants of the theorem include multiple and even infinitely many indepen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Double-precision Floating-point Format
Double-precision floating-point format (sometimes called FP64 or float64) is a floating-point number format, usually occupying 64 bits in computer memory; it represents a wide range of numeric values by using a floating radix point. Double precision may be chosen when the range or precision of single precision would be insufficient. In the IEEE 754 standard, the 64-bit base-2 format is officially referred to as binary64; it was called double in IEEE 754-1985. IEEE 754 specifies additional floating-point formats, including 32-bit base-2 ''single precision'' and, more recently, base-10 representations (decimal floating point). One of the first programming languages to provide floating-point data types was Fortran. Before the widespread adoption of IEEE 754-1985, the representation and properties of floating-point data types depended on the computer manufacturer and computer model, and upon decisions made by programming-language implementers. E.g., GW-BASIC's double-precision ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chimpanzee Seated At Typewriter
The chimpanzee (; ''Pan troglodytes''), also simply known as the chimp, is a species of great ape native to the forests and savannahs of tropical Africa. It has four confirmed subspecies and a fifth proposed one. When its close relative the bonobo was more commonly known as the pygmy chimpanzee, this species was often called the common chimpanzee or the robust chimpanzee. The chimpanzee and the bonobo are the only species in the genus ''Pan''. Evidence from fossils and DNA sequencing shows that ''Pan'' is a sister taxon to the human lineage and is thus humans' closest living relative. The chimpanzee is covered in coarse black hair but has a bare face, fingers, toes, palms of the hands, and soles of the feet. It is larger and more robust than the bonobo, weighing for males and for females and standing . The chimpanzee lives in groups that range in size from 15 to 150 members, although individuals travel and forage in much smaller groups during the day. The species lives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Card Shuffle
Shuffling is a technique used to randomize a deck of playing cards, introducing an element of chance into card games. Various shuffling methods exist, each with its own characteristics and potential for manipulation. One of the simplest shuffling techniques is the overhand shuffle, where small packets of cards are transferred from one hand to the other. This method is easy to perform but can be manipulated to control the order of cards. Another common technique is the riffle shuffle, where the deck is split into two halves and interleaved. This method is more complex but minimizes the risk of exposing cards. The Gilbert–Shannon–Reeds model suggests that seven riffle shuffles are sufficient to thoroughly randomize a deck, although some studies indicate that six shuffles may be enough. Other shuffling methods include the Hindu shuffle, commonly used in Asia, and the pile shuffle, where cards are dealt into piles and then stacked. The Mongean shuffle involves a specific seq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
IEEE Floating-point
The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point arithmetic originally established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating-point implementations that made them difficult to use reliably and portably. Many hardware floating-point units use the IEEE 754 standard. The standard defines: * ''arithmetic formats:'' sets of binary and decimal floating-point data, which consist of finite numbers (including signed zeros and subnormal numbers), infinities, and special "not a number" values ( NaNs) * ''interchange formats:'' encodings (bit strings) that may be used to exchange floating-point data in an efficient and compact form * ''rounding rules:'' properties to be satisfied when rounding numbers during arithmetic and conversions * ''operations:'' arithmetic and other operations (such as trigonometric functions) on arithmetic format ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Single-precision Floating-point Format
Single-precision floating-point format (sometimes called FP32 or float32) is a computer number format, usually occupying 32 bits in computer memory; it represents a wide dynamic range of numeric values by using a floating radix point. A floating-point variable can represent a wider range of numbers than a fixed-point variable of the same bit width at the cost of precision. A signed 32-bit integer variable has a maximum value of 231 − 1 = 2,147,483,647, whereas an IEEE 754 32-bit base-2 floating-point variable has a maximum value of (2 − 2−23) × 2127 ≈ 3.4028235 × 1038. All integers with seven or fewer decimal digits, and any 2''n'' for a whole number −149 ≤ ''n'' ≤ 127, can be converted exactly into an IEEE 754 single-precision floating-point value. In the IEEE 754 standard, the 32-bit base-2 format is officially referred to as binary32; it was called single in IEEE 754-1985. IEEE 754 specifies additional floating-point types, such as 64-bit base-2 ''doubl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Extended Precision
Extended precision refers to floating-point number formats that provide greater precision than the basic floating-point formats. Extended-precision formats support a basic format by minimizing roundoff and overflow errors in intermediate values of expressions on the base format. In contrast to ''extended precision'', arbitrary-precision arithmetic refers to implementations of much larger numeric types (with a storage count that usually is not a power of two) using special software (or, rarely, hardware). Extended-precision implementations There is a long history of extended floating-point formats reaching back nearly to the middle of the last century.. Various manufacturers have used different formats for extended precision for different machines. In many cases the format of the extended precision is not quite the same as a scale-up of the ordinary single- and double-precision formats it is meant to extend. In a few cases the implementation was merely a software-based change i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Standard 52-card Deck
The standard 52-card deck of French-suited playing cards is the most common pack of playing cards used today. The main feature of most playing card decks that empower their use in diverse games and other activities is their double-sided design, where one side, usually bearing a colourful or complex pattern, is exactly identical on all playing cards, thus ensuring the anonymity and fungibility of the cards when their value is to be kept secret, and a second side, that, when apparent, is unique to every individual card in a deck, usually bearing a suit as well as an alphanumerical value, which may be used to distinguish the card in game mechanics. In English-speaking countries it is the only traditional pack used for playing cards; in many countries, however, it is used alongside other traditional, often older, standard packs with different suit systems such as those with German-, Italian-, Spanish- or Swiss suits. The most common pattern of French-suited cards worldwide and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Shuffling
Shuffling is a technique used to randomize a deck of playing cards, introducing an element of chance into card games. Various shuffling methods exist, each with its own characteristics and potential for manipulation. One of the simplest shuffling techniques is the overhand shuffle, where small packets of cards are transferred from one hand to the other. This method is easy to perform but can be manipulated to control the order of cards. Another common technique is the riffle shuffle, where the deck is split into two halves and interleaved. This method is more complex but minimizes the risk of exposing cards. The Gilbert–Shannon–Reeds model suggests that seven riffle shuffles are sufficient to thoroughly randomize a deck, although some studies indicate that six shuffles may be enough. Other shuffling methods include the Hindu shuffle, commonly used in Asia, and the pile shuffle, where cards are dealt into piles and then stacked. The Mongean shuffle involves a specific seq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an event is to occur."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th ed., (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', vol. 1, 3rd ed., (1968), Wiley, . This number is often expressed as a percentage (%), ranging from 0% to 100%. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written as 0.5 or 50%). These concepts have been given an axiomatic mathematical formaliza ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Monkey
Monkey is a common name that may refer to most mammals of the infraorder Simiiformes, also known as simians. Traditionally, all animals in the group now known as simians are counted as monkeys except the apes. Thus monkeys, in that sense, constitute an incomplete paraphyletic grouping; alternatively, if apes (Hominoidea) are included, ''monkeys'' and ''simians'' are synonyms. In 1812, Étienne Geoffroy grouped the apes and the Cercopithecidae group of monkeys together and established the name Catarrhini, "Old World monkeys" ("''singes de l'Ancien Monde''" in French). The extant sister of the Catarrhini in the monkey ("singes") group is the Platyrrhini (New World monkeys). Some nine million years before the divergence between the Cercopithecidae and the apes, the Platyrrhini emerged within "monkeys" by migration to South America likely by ocean. Apes are thus deep in the tree of extant and extinct monkeys, and any of the apes is distinctly closer related to the Cercopith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
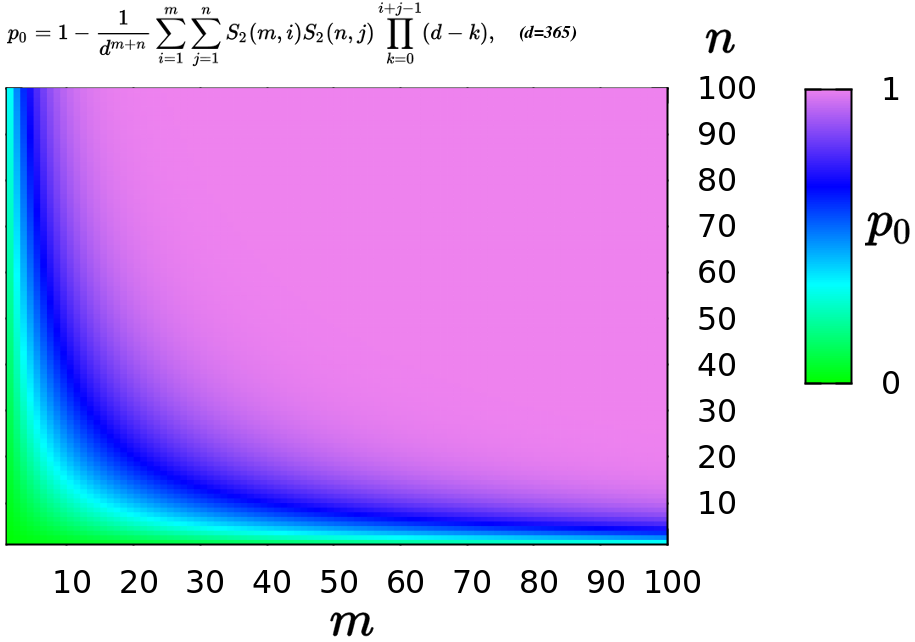
Birthday Problem
In probability theory, the birthday problem asks for the probability that, in a set of randomly chosen people, at least two will share the same birthday. The birthday paradox is the counterintuitive fact that only 23 people are needed for that probability to exceed 50%. The birthday paradox is a veridical paradox: it seems wrong at first glance but is, in fact, true. While it may seem surprising that only 23 individuals are required to reach a 50% probability of a shared birthday, this result is made more intuitive by considering that the birthday comparisons will be made between every possible pair of individuals. With 23 individuals, there are = 253 pairs to consider. Real-world applications for the birthday problem include a cryptographic attack called the birthday attack, which uses this probabilistic model to reduce the complexity of finding a Collision attack, collision for a hash function, as well as calculating the approximate risk of a hash collision existi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |