Cellular Automaton on:
[Wikipedia]
[Google]
[Amazon]
 A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete
 Cellular automata are often simulated on a finite grid rather than an infinite one. In two dimensions, the universe would be a rectangle instead of an infinite plane. The obvious problem with finite grids is how to handle the cells on the edges. How they are handled will affect the values of all the cells in the grid. One possible method is to allow the values in those cells to remain constant. Another method is to define neighborhoods differently for these cells. One could say that they have fewer neighbors, but then one would also have to define new rules for the cells located on the edges. These cells are usually handled with periodic boundary conditions resulting in a ''toroidal'' arrangement: when one goes off the top, one comes in at the corresponding position on the bottom, and when one goes off the left, one comes in on the right. (This essentially simulates an infinite periodic tiling, and in the field of
Cellular automata are often simulated on a finite grid rather than an infinite one. In two dimensions, the universe would be a rectangle instead of an infinite plane. The obvious problem with finite grids is how to handle the cells on the edges. How they are handled will affect the values of all the cells in the grid. One possible method is to allow the values in those cells to remain constant. Another method is to define neighborhoods differently for these cells. One could say that they have fewer neighbors, but then one would also have to define new rules for the cells located on the edges. These cells are usually handled with periodic boundary conditions resulting in a ''toroidal'' arrangement: when one goes off the top, one comes in at the corresponding position on the bottom, and when one goes off the left, one comes in on the right. (This essentially simulates an infinite periodic tiling, and in the field of
 Ulam and von Neumann created a method for calculating liquid motion in the late 1950s. The driving concept of the method was to consider a liquid as a group of discrete units and calculate the motion of each based on its neighbors' behaviors. Thus was born the first system of cellular automata. Like Ulam's lattice network, von Neumann's cellular automata are two-dimensional, with his self-replicator implemented algorithmically. The result was a universal copier and constructor working within a cellular automaton with a small neighborhood (only those cells that touch are neighbors; for von Neumann's cellular automata, only
Ulam and von Neumann created a method for calculating liquid motion in the late 1950s. The driving concept of the method was to consider a liquid as a group of discrete units and calculate the motion of each based on its neighbors' behaviors. Thus was born the first system of cellular automata. Like Ulam's lattice network, von Neumann's cellular automata are two-dimensional, with his self-replicator implemented algorithmically. The result was a universal copier and constructor working within a cellular automaton with a small neighborhood (only those cells that touch are neighbors; for von Neumann's cellular automata, only
 One way is by using something other than a rectangular (cubic, ''etc.'') grid. For example, if a plane is tiled with regular hexagons, those hexagons could be used as cells. In many cases the resulting cellular automata are equivalent to those with rectangular grids with specially designed neighborhoods and rules. Another variation would be to make the grid itself irregular, such as with Penrose tiles.
Also, rules can be probabilistic rather than deterministic. Such cellular automata are called probabilistic cellular automata. A probabilistic rule gives, for each pattern at time ''t'', the probabilities that the central cell will transition to each possible state at time ''t'' + 1. Sometimes a simpler rule is used; for example: "The rule is the Game of Life, but on each time step there is a 0.001% probability that each cell will transition to the opposite color."
The neighborhood or rules could change over time or space. For example, initially the new state of a cell could be determined by the horizontally adjacent cells, but for the next generation the vertical cells would be used.
In cellular automata, the new state of a cell is not affected by the new state of other cells. This could be changed so that, for instance, a 2 by 2 block of cells can be determined by itself and the cells adjacent to itself.
There are '' continuous automata''. These are like totalistic cellular automata, but instead of the rule and states being discrete (''e.g.'' a table, using states ), continuous functions are used, and the states become continuous (usually values in ,1. The state of a location is a finite number of real numbers. Certain cellular automata can yield diffusion in liquid patterns in this way.
Continuous spatial automata have a continuum of locations. The state of a location is a finite number of real numbers. Time is also continuous, and the state evolves according to differential equations. One important example is reaction–diffusion textures, differential equations proposed by
One way is by using something other than a rectangular (cubic, ''etc.'') grid. For example, if a plane is tiled with regular hexagons, those hexagons could be used as cells. In many cases the resulting cellular automata are equivalent to those with rectangular grids with specially designed neighborhoods and rules. Another variation would be to make the grid itself irregular, such as with Penrose tiles.
Also, rules can be probabilistic rather than deterministic. Such cellular automata are called probabilistic cellular automata. A probabilistic rule gives, for each pattern at time ''t'', the probabilities that the central cell will transition to each possible state at time ''t'' + 1. Sometimes a simpler rule is used; for example: "The rule is the Game of Life, but on each time step there is a 0.001% probability that each cell will transition to the opposite color."
The neighborhood or rules could change over time or space. For example, initially the new state of a cell could be determined by the horizontally adjacent cells, but for the next generation the vertical cells would be used.
In cellular automata, the new state of a cell is not affected by the new state of other cells. This could be changed so that, for instance, a 2 by 2 block of cells can be determined by itself and the cells adjacent to itself.
There are '' continuous automata''. These are like totalistic cellular automata, but instead of the rule and states being discrete (''e.g.'' a table, using states ), continuous functions are used, and the states become continuous (usually values in ,1. The state of a location is a finite number of real numbers. Certain cellular automata can yield diffusion in liquid patterns in this way.
Continuous spatial automata have a continuum of locations. The state of a location is a finite number of real numbers. Time is also continuous, and the state evolves according to differential equations. One important example is reaction–diffusion textures, differential equations proposed by
considers continuous spatial automata as a model of computation. There are known examples of continuous spatial automata, which exhibit propagating phenomena analogous to gliders in the Game of Life. ''Graph rewriting automata'' are extensions of cellular automata based on graph rewriting systems.
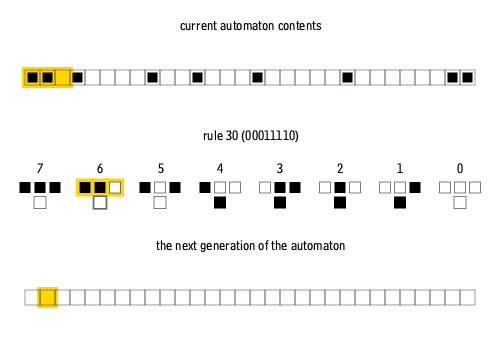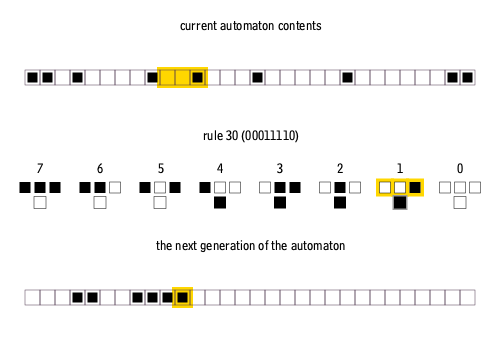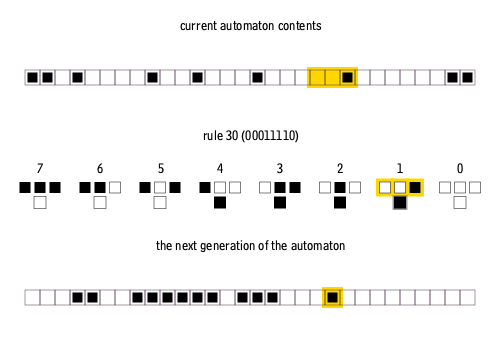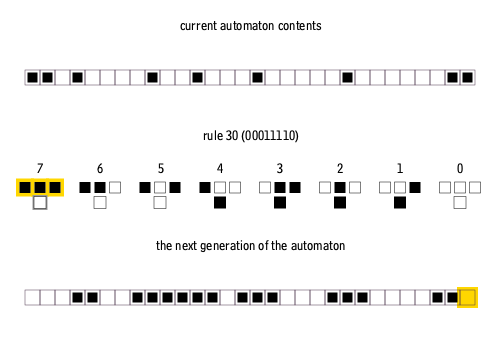 These 256 cellular automata are generally referred to by their Wolfram code, a standard naming convention invented by Wolfram that gives each rule a number from 0 to 255. A number of papers have analyzed and compared the distinct cases among the 256 cellular automata (many are trivially isomorphic). The rule 30, rule 90, rule 110, and rule 184 cellular automata are particularly interesting. The images below show the history of rules 30 and 110 when the starting configuration consists of a 1 (at the top of each image) surrounded by 0s. Each row of pixels represents a generation in the history of the automaton, with ''t''=0 being the top row. Each pixel is colored white for 0 and black for 1.
These 256 cellular automata are generally referred to by their Wolfram code, a standard naming convention invented by Wolfram that gives each rule a number from 0 to 255. A number of papers have analyzed and compared the distinct cases among the 256 cellular automata (many are trivially isomorphic). The rule 30, rule 90, rule 110, and rule 184 cellular automata are particularly interesting. The images below show the history of rules 30 and 110 when the starting configuration consists of a 1 (at the top of each image) surrounded by 0s. Each row of pixels represents a generation in the history of the automaton, with ''t''=0 being the top row. Each pixel is colored white for 0 and black for 1.
 Rule 30 exhibits ''class 3'' behavior, meaning even simple input patterns such as that shown lead to chaotic, seemingly random histories.
Rule 110, like the Game of Life, exhibits what Wolfram calls ''class 4'' behavior, which is neither completely random nor completely repetitive. Localized structures appear and interact in various complicated-looking ways. In the course of the development of '' A New Kind of Science'', as a research assistant to Wolfram in 1994, Matthew Cook proved that some of these structures were rich enough to support universality. This result is interesting because rule 110 is an extremely simple one-dimensional system, and difficult to engineer to perform specific behavior. This result therefore provides significant support for Wolfram's view that class 4 systems are inherently likely to be universal. Cook presented his proof at a
Rule 30 exhibits ''class 3'' behavior, meaning even simple input patterns such as that shown lead to chaotic, seemingly random histories.
Rule 110, like the Game of Life, exhibits what Wolfram calls ''class 4'' behavior, which is neither completely random nor completely repetitive. Localized structures appear and interact in various complicated-looking ways. In the course of the development of '' A New Kind of Science'', as a research assistant to Wolfram in 1994, Matthew Cook proved that some of these structures were rich enough to support universality. This result is interesting because rule 110 is an extremely simple one-dimensional system, and difficult to engineer to perform specific behavior. This result therefore provides significant support for Wolfram's view that class 4 systems are inherently likely to be universal. Cook presented his proof at a
 Several biological processes occur—or can be simulated—by cellular automata.
Some examples of biological phenomena modeled by cellular automata with a simple state space are:
* Patterns of some
Several biological processes occur—or can be simulated—by cellular automata.
Some examples of biological phenomena modeled by cellular automata with a simple state space are:
* Patterns of some
 Probabilistic cellular automata are used in
Probabilistic cellular automata are used in
Mirek's Cellebration
– Home to free cellular automata explorer software, "MCell". The software supports a large number of 1D and 2D rules. The site provides both an extensive rules lexicon and many image galleries loaded with examples of rules. Source code (Javascript) is available.
Golly
supports von Neumann, Nobili, GOL, and a great many other systems of cellular automata. Developed by Tomas Rokicki and Andrew Trevorrow. This is the only simulator currently available that can demonstrate von Neumann type self-replication.
– An atlas of various types of one-dimensional cellular automata.
Conway LifeCellular automaton FAQ
from the newsgroup comp.theory.cell-automata
(includes discussion on triangular grids, and larger neighborhood CAs)
contains an extensive list of academic and professional reference material. {{Authority control Systems theory Dynamical systems Computational fields of study
 A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation
In computer science, and more specifically in computability theory and computational complexity theory, a model of computation is a model which describes how an output of a mathematical function is computed given an input. A model describes how ...
studied in automata theory
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to cognitive science and mathematical l ...
. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, theoretical biology and microstructure
Microstructure is the very small scale structure of a material, defined as the structure of a prepared surface of material as revealed by an optical microscope above 25× magnification. The microstructure of a material (such as metals, polymer ...
modeling.
A cellular automaton consists of a regular grid of ''cells'', each in one of a finite number of ''states
State most commonly refers to:
* State (polity), a centralized political organization that regulates law and society within a territory
**Sovereign state, a sovereign polity in international law, commonly referred to as a country
**Nation state, a ...
'', such as ''on'' and ''off'' (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its ''neighborhood'' is defined relative to the specified cell. An initial state (time ''t'' = 0) is selected by assigning a state for each cell. A new ''generation'' is created (advancing ''t'' by 1), according to some fixed ''rule'' (generally, a mathematical function) that determines the new state of each cell in terms of the current state of the cell and the states of the cells in its neighborhood. Typically, the rule for updating the state of cells is the same for each cell and does not change over time, and is applied to the whole grid simultaneously, though exceptions are known, such as the stochastic cellular automaton and asynchronous cellular automaton.
The concept was originally discovered in the 1940s by Stanislaw Ulam and John von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, in ...
while they were contemporaries at Los Alamos National Laboratory
Los Alamos National Laboratory (often shortened as Los Alamos and LANL) is one of the sixteen research and development Laboratory, laboratories of the United States Department of Energy National Laboratories, United States Department of Energy ...
. While studied by some throughout the 1950s and 1960s, it was not until the 1970s and Conway's Game of Life
The Game of Life, also known as Conway's Game of Life or simply Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial ...
, a two-dimensional cellular automaton, that interest in the subject expanded beyond academia. In the 1980s, Stephen Wolfram
Stephen Wolfram ( ; born 29 August 1959) is a British-American computer scientist, physicist, and businessman. He is known for his work in computer algebra and theoretical physics. In 2012, he was named a fellow of the American Mathematical So ...
engaged in a systematic study of one-dimensional cellular automata, or what he calls elementary cellular automata; his research assistant Matthew Cook showed that one of these rules is Turing-complete
In computability theory, a system of data-manipulation rules (such as a model of computation, a computer's instruction set, a programming language, or a cellular automaton) is said to be Turing-complete or computationally universal if it can be ...
.
The primary classifications of cellular automata, as outlined by Wolfram, are numbered one to four. They are, in order, automata in which patterns generally stabilize into homogeneity
Homogeneity and heterogeneity are concepts relating to the Uniformity (chemistry), uniformity of a Chemical substance, substance, process or image. A homogeneous feature is uniform in composition or character (i.e., color, shape, size, weight, ...
, automata in which patterns evolve into mostly stable or oscillating structures, automata in which patterns evolve in a seemingly chaotic fashion, and automata in which patterns become extremely complex and may last for a long time, with stable local structures. This last class is thought to be computationally universal, or capable of simulating a Turing machine
A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algori ...
. Special types of cellular automata are '' reversible'', where only a single configuration leads directly to a subsequent one, and ''totalistic'', in which the future value of individual cells only depends on the total value of a group of neighboring cells. Cellular automata can simulate a variety of real-world systems, including biological and chemical ones.
Overview
One way to simulate a two-dimensional cellular automaton is with an infinite sheet of graph paper along with a set of rules for the cells to follow. Each square is called a "cell" and each cell has two possible states, black or white. The ''neighborhood'' of a cell is the nearby, usually adjacent, cells. The two most common types of neighborhoods are the '' von Neumann neighborhood'' and the '' Moore neighborhood''. The former, named after the founding cellular automaton theorist, consists of the fourorthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...
ly adjacent cells. The latter includes the von Neumann neighborhood as well as the four diagonally adjacent cells. For such a cell and its Moore neighborhood, there are 512 (= 29) possible patterns. For each of the 512 possible patterns, the rule table would state whether the center cell will be black or white on the next time interval. Conway's Game of Life
The Game of Life, also known as Conway's Game of Life or simply Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial ...
is a popular version of this model. Another common neighborhood type is the ''extended von Neumann neighborhood'', which includes the two closest cells in each orthogonal direction, for a total of eight. The general equation for the total number of automata possible is ''k''''k''''s'', where ''k'' is the number of possible states for a cell, and ''s'' is the number of neighboring cells (including the cell to be calculated itself) used to determine the cell's next state. Thus, in the two-dimensional system with a Moore neighborhood, the total number of automata possible would be 229, or .
It is usually assumed that every cell in the universe starts in the same state, except for a finite number of cells in other states; the assignment of state values is called a ''configuration''. More generally, it is sometimes assumed that the universe starts out covered with a periodic pattern, and only a finite number of cells violate that pattern. The latter assumption is common in one-dimensional cellular automata.
 Cellular automata are often simulated on a finite grid rather than an infinite one. In two dimensions, the universe would be a rectangle instead of an infinite plane. The obvious problem with finite grids is how to handle the cells on the edges. How they are handled will affect the values of all the cells in the grid. One possible method is to allow the values in those cells to remain constant. Another method is to define neighborhoods differently for these cells. One could say that they have fewer neighbors, but then one would also have to define new rules for the cells located on the edges. These cells are usually handled with periodic boundary conditions resulting in a ''toroidal'' arrangement: when one goes off the top, one comes in at the corresponding position on the bottom, and when one goes off the left, one comes in on the right. (This essentially simulates an infinite periodic tiling, and in the field of
Cellular automata are often simulated on a finite grid rather than an infinite one. In two dimensions, the universe would be a rectangle instead of an infinite plane. The obvious problem with finite grids is how to handle the cells on the edges. How they are handled will affect the values of all the cells in the grid. One possible method is to allow the values in those cells to remain constant. Another method is to define neighborhoods differently for these cells. One could say that they have fewer neighbors, but then one would also have to define new rules for the cells located on the edges. These cells are usually handled with periodic boundary conditions resulting in a ''toroidal'' arrangement: when one goes off the top, one comes in at the corresponding position on the bottom, and when one goes off the left, one comes in on the right. (This essentially simulates an infinite periodic tiling, and in the field of partial differential equations
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to how ...
is sometimes referred to as ''periodic'' boundary conditions.) This can be visualized as taping the left and right edges of the rectangle to form a tube, then taping the top and bottom edges of the tube to form a torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu ...
(doughnut shape). Universes of other dimensions are handled similarly. This solves boundary problems with neighborhoods, but another advantage is that it is easily programmable using modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic operations for integers, other than the usual ones from elementary arithmetic, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to mo ...
functions. For example, in a 1-dimensional cellular automaton like the examples below, the neighborhood of a cell ''xit'' is , where ''t'' is the time step (vertical), and ''i'' is the index (horizontal) in one generation.
History
Stanislaw Ulam, while working at theLos Alamos National Laboratory
Los Alamos National Laboratory (often shortened as Los Alamos and LANL) is one of the sixteen research and development Laboratory, laboratories of the United States Department of Energy National Laboratories, United States Department of Energy ...
in the 1940s, studied the growth of crystals, using a simple lattice network as his model. At the same time, John von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, in ...
, Ulam's colleague at Los Alamos, was working on the problem of self-replicating systems. Von Neumann's initial design was founded upon the notion of one robot building another robot. This design is known as the kinematic model. As he developed this design, von Neumann came to realize the great difficulty of building a self-replicating robot, and of the great cost in providing the robot with a "sea of parts" from which to build its replicant. Neumann wrote a paper entitled "The general and logical theory of automata" for the Hixon Symposium in 1948. Ulam was the one who suggested using a ''discrete'' system for creating a reductionist model of self-replication. Nils Aall Barricelli performed many of the earliest explorations of these models of artificial life
Artificial life (ALife or A-Life) is a field of study wherein researchers examine systems related to natural life, its processes, and its evolution, through the use of simulations with computer models, robotics, and biochemistry. The discipline ...
.
 Ulam and von Neumann created a method for calculating liquid motion in the late 1950s. The driving concept of the method was to consider a liquid as a group of discrete units and calculate the motion of each based on its neighbors' behaviors. Thus was born the first system of cellular automata. Like Ulam's lattice network, von Neumann's cellular automata are two-dimensional, with his self-replicator implemented algorithmically. The result was a universal copier and constructor working within a cellular automaton with a small neighborhood (only those cells that touch are neighbors; for von Neumann's cellular automata, only
Ulam and von Neumann created a method for calculating liquid motion in the late 1950s. The driving concept of the method was to consider a liquid as a group of discrete units and calculate the motion of each based on its neighbors' behaviors. Thus was born the first system of cellular automata. Like Ulam's lattice network, von Neumann's cellular automata are two-dimensional, with his self-replicator implemented algorithmically. The result was a universal copier and constructor working within a cellular automaton with a small neighborhood (only those cells that touch are neighbors; for von Neumann's cellular automata, only orthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...
cells), and with 29 states per cell. Von Neumann gave an existence proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object by creating or providing a method for creating the object. This is in contrast to a non-constructive proof (also known as an existen ...
that a particular pattern would make endless copies of itself within the given cellular universe by designing a 200,000 cell configuration that could do so. This design is known as the tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety ...
model, and is called a von Neumann universal constructor.
Also in the 1940s, Norbert Wiener
Norbert Wiener (November 26, 1894 – March 18, 1964) was an American computer scientist, mathematician, and philosopher. He became a professor of mathematics at the Massachusetts Institute of Technology ( MIT). A child prodigy, Wiener late ...
and Arturo Rosenblueth developed a model of excitable media with some of the characteristics of a cellular automaton. Their specific motivation was the mathematical description of impulse conduction in cardiac systems. However their model is not a cellular automaton because the medium in which signals propagate is continuous, and wave fronts are curves. A true cellular automaton model of excitable media was developed and studied by J. M. Greenberg and S. P. Hastings in 1978; see Greenberg-Hastings cellular automaton. The original work of Wiener and Rosenblueth contains many insights and continues to be cited in modern research publications on cardiac arrhythmia
Arrhythmias, also known as cardiac arrhythmias, are irregularities in the heartbeat, including when it is too fast or too slow. Essentially, this is anything but normal sinus rhythm. A resting heart rate that is too fast – above 100 beat ...
and excitable systems.
In the 1960s, cellular automata were studied as a particular type of dynamical system
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models ...
and the connection with the mathematical field of symbolic dynamics
In mathematics, symbolic dynamics is the study of dynamical systems defined on a discrete space consisting of infinite sequences of abstract symbols. The evolution of the dynamical system is defined as a simple shift of the sequence.
Because of t ...
was established for the first time. In 1969, Gustav A. Hedlund compiled many results following this point of view in what is still considered as a seminal paper for the mathematical study of cellular automata. The most fundamental result is the characterization in the Curtis–Hedlund–Lyndon theorem of the set of global rules of cellular automata as the set of continuous endomorphisms of shift space
Shift may refer to:
Art, entertainment, and media Gaming
* ''Shift'' (series), a 2008 online video game series by Armor Games
* '' Need for Speed: Shift'', a 2009 racing video game
** '' Shift 2: Unleashed'', its 2011 sequel
Literature
* ''S ...
s.
In 1969, German computer pioneer Konrad Zuse
Konrad Ernst Otto Zuse (; ; 22 June 1910 – 18 December 1995) was a German civil engineer, List of pioneers in computer science, pioneering computer scientist, inventor and businessman. His greatest achievement was the world's first programm ...
published his book '' Calculating Space'', proposing that the physical laws of the universe are discrete by nature, and that the entire universe is the output of a deterministic computation on a single cellular automaton; "Zuse's Theory" became the foundation of the field of study called '' digital physics''.
Also in 1969 computer scientist Alvy Ray Smith
Alvy Ray Smith III (born September 8, 1943) is an American computer scientist who co-founded Lucasfilm's Computer Division and Pixar, participating in the 1980s and 1990s expansion of computer animation into feature film.
He is one of the 50 F ...
completed a Stanford PhD dissertation on Cellular Automata Theory, the first mathematical treatment of CA as a general class of computers. Many papers came from this dissertation: He showed the equivalence of neighborhoods of various shapes, how to reduce a Moore to a von Neumann neighborhood or how to reduce any neighborhood to a von Neumann neighborhood. He proved that two-dimensional CA are computation universal, introduced 1-dimensional CA, and showed that they too are computation universal, even with simple neighborhoods. He showed how to subsume the complex von Neumann proof of construction universality (and hence self-reproducing machines) into a consequence of computation universality in a 1-dimensional CA. Intended as the introduction to the German edition of von Neumann's book on CA, he wrote a survey of the field with dozens of references to papers, by many authors in many countries over a decade or so of work, often overlooked by modern CA researchers.
In the 1970s a two-state, two-dimensional cellular automaton named Game of Life became widely known, particularly among the early computing community. Invented by John Conway and popularized by Martin Gardner
Martin Gardner (October 21, 1914May 22, 2010) was an American popular mathematics and popular science writer with interests also encompassing magic, scientific skepticism, micromagic, philosophy, religion, and literatureespecially the writin ...
in a ''Scientific American
''Scientific American'', informally abbreviated ''SciAm'' or sometimes ''SA'', is an American popular science magazine. Many scientists, including Albert Einstein and Nikola Tesla, have contributed articles to it, with more than 150 Nobel Pri ...
'' article, its rules are as follows:
# Any live cell with fewer than two live neighbours dies, as if caused by underpopulation.
# Any live cell with two or three live neighbours lives on to the next generation.
# Any live cell with more than three live neighbours dies, as if by overpopulation.
# Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.
Despite its simplicity, the system achieves an impressive diversity of behavior, fluctuating between apparent randomness
In common usage, randomness is the apparent or actual lack of definite pattern or predictability in information. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. ...
and order. One of the most apparent features of the Game of Life is the frequent occurrence of ''gliders'', arrangements of cells that essentially move themselves across the grid. It is possible to arrange the automaton so that the gliders interact to perform computations, and after much effort it has been shown that the Game of Life can emulate a universal Turing machine
In computer science, a universal Turing machine (UTM) is a Turing machine capable of computing any computable sequence, as described by Alan Turing in his seminal paper "On Computable Numbers, with an Application to the Entscheidungsproblem". Co ...
. It was viewed as a largely recreational topic, and little follow-up work was done outside of investigating the particularities of the Game of Life and a few related rules in the early 1970s.
Stephen Wolfram
Stephen Wolfram ( ; born 29 August 1959) is a British-American computer scientist, physicist, and businessman. He is known for his work in computer algebra and theoretical physics. In 2012, he was named a fellow of the American Mathematical So ...
independently began working on cellular automata in mid-1981 after considering how complex patterns seemed formed in nature in violation of the second law of thermodynamics
The second law of thermodynamics is a physical law based on Universal (metaphysics), universal empirical observation concerning heat and Energy transformation, energy interconversions. A simple statement of the law is that heat always flows spont ...
. His investigations were initially spurred by a desire to model systems such as the neural networks
A neural network is a group of interconnected units called neurons that send signals to one another. Neurons can be either Cell (biology), biological cells or signal pathways. While individual neurons are simple, many of them together in a netwo ...
found in brains. He published his first paper in ''Reviews of Modern Physics
''Reviews of Modern Physics'' (often abbreviated RMP) is a quarterly Peer review, peer-reviewed scientific journal published by the American Physical Society. It was established in 1929 and the current editor-in-chief is Michael Thoennessen. The jo ...
'' investigating '' elementary cellular automata'' ( Rule 30 in particular) in June 1983. The unexpected complexity of the behavior of these simple rules led Wolfram to suspect that complexity in nature may be due to similar mechanisms. His investigations, however, led him to realize that cellular automata were poor at modelling neural networks. Additionally, during this period Wolfram formulated the concepts of intrinsic randomness
In common usage, randomness is the apparent or actual lack of definite pattern or predictability in information. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. ...
and computational irreducibility, and suggested that rule 110 may be universal—a fact proved later by Wolfram's research assistant Matthew Cook in the 1990s.
Classification
Wolfram, in '' A New Kind of Science'' and several papers dating from the mid-1980s, defined four classes into which cellular automata and several other simple computational models can be divided depending on their behavior. While earlier studies in cellular automata tended to try to identify types of patterns for specific rules, Wolfram's classification was the first attempt to classify the rules themselves. In order of complexity the classes are: *Class 1: Nearly all initial patterns evolve quickly into a stable, homogeneous state. Any randomness in the initial pattern disappears. *Class 2: Nearly all initial patterns evolve quickly into stable or oscillating structures. Some of the randomness in the initial pattern may filter out, but some remains. Local changes to the initial pattern tend to remain local. *Class 3: Nearly all initial patterns evolve in a pseudo-random or chaotic manner. Any stable structures that appear are quickly destroyed by the surrounding noise. Local changes to the initial pattern tend to spread indefinitely. *Class 4: Nearly all initial patterns evolve into structures that interact in complex and interesting ways, with the formation of local structures that are able to survive for long periods of time. Class 2 type stable or oscillating structures may be the eventual outcome, but the number of steps required to reach this state may be very large, even when the initial pattern is relatively simple. Local changes to the initial pattern may spread indefinitely. Wolfram hasconjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's conjecture (now a theorem, proven in 1995 by Andrew Wiles), ha ...
d that many class 4 cellular automata, if not all, are capable of universal computation. This has been proven for Rule 110 and Conway's Game of Life.
These definitions are qualitative in nature and there is some room for interpretation. According to Wolfram, "...with almost any general classification scheme there are inevitably cases which get assigned to one class by one definition and another class by another definition. And so it is with cellular automata: there are occasionally rules...that show some features of one class and some of another." Wolfram's classification has been empirically matched to a clustering of the compressed lengths of the outputs of cellular automata.
There have been several attempts to classify cellular automata in formally rigorous classes, inspired by Wolfram's classification. For instance, Culik and Yu proposed three well-defined classes (and a fourth one for the automata not matching any of these), which are sometimes called Culik–Yu classes; membership in these proved undecidable.
Wolfram's class 2 can be partitioned into two subgroups of stable (fixed-point) and oscillating (periodic) rules.
The idea that there are 4 classes of dynamical system came originally from Nobel-prize winning chemist Ilya Prigogine
Viscount Ilya Romanovich Prigogine (; ; 28 May 2003) was a Belgian physical chemist of Russian-Jewish origin, noted for his work on dissipative structures, complex systems, and irreversibility.
Prigogine's work most notably earned him the 19 ...
who identified these 4 classes of thermodynamical systems: (1) systems in thermodynamic equilibrium, (2) spatially/temporally uniform systems, (3) chaotic systems, and (4) complex far-from-equilibrium systems with dissipative structures (see figure 1 in the 1974 paper of Nicolis, Prigogine's student).
Reversible
A cellular automaton is ''reversible'' if, for every current configuration of the cellular automaton, there is exactly one past configuration (preimage
In mathematics, for a function f: X \to Y, the image of an input value x is the single output value produced by f when passed x. The preimage of an output value y is the set of input values that produce y.
More generally, evaluating f at each ...
). If one thinks of a cellular automaton as a function mapping configurations to configurations, reversibility implies that this function is bijective
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equival ...
. If a cellular automaton is reversible, its time-reversed behavior can also be described as a cellular automaton; this fact is a consequence of the Curtis–Hedlund–Lyndon theorem, a topological characterization of cellular automata. For cellular automata in which not every configuration has a preimage, the configurations without preimages are called ''Garden of Eden
In Abrahamic religions, the Garden of Eden (; ; ) or Garden of God ( and ), also called the Terrestrial Paradise, is the biblical paradise described in Genesis 2–3 and Ezekiel 28 and 31..
The location of Eden is described in the Book of Ge ...
'' patterns.
For one-dimensional cellular automata there are known algorithms for deciding whether a rule is reversible or irreversible. However, for cellular automata of two or more dimensions reversibility is undecidable; that is, there is no algorithm that takes as input an automaton rule and is guaranteed to determine correctly whether the automaton is reversible. The proof by Jarkko Kari is related to the tiling problem by Wang tile
Wang tiles (or Wang dominoes), first proposed by mathematician, logician, and philosopher Hao Wang in 1961, is a class of formal systems. They are modeled visually by square tiles with a color on each side. A set of such tiles is selected, and ...
s.
Reversible cellular automata are often used to simulate such physical phenomena as gas and fluid dynamics, since they obey the laws of thermodynamics
Thermodynamics is a branch of physics that deals with heat, Work (thermodynamics), work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed b ...
. Such cellular automata have rules specially constructed to be reversible. Such systems have been studied by Tommaso Toffoli, Norman Margolus and others. Several techniques can be used to explicitly construct reversible cellular automata with known inverses. Two common ones are the second-order cellular automaton and the block cellular automaton, both of which involve modifying the definition of a cellular automaton in some way. Although such automata do not strictly satisfy the definition given above, it can be shown that they can be emulated by conventional cellular automata with sufficiently large neighborhoods and numbers of states, and can therefore be considered a subset of conventional cellular automata. Conversely, it has been shown that every reversible cellular automaton can be emulated by a block cellular automaton.
Totalistic
A special class of cellular automata are ''totalistic'' cellular automata. The state of each cell in a totalistic cellular automaton is represented by a number (usually an integer value drawn from a finite set), and the value of a cell at time ''t'' depends only on the ''sum'' of the values of the cells in its neighborhood (possibly including the cell itself) at time ''t'' − 1. If the state of the cell at time ''t'' depends on both its own state and the total of its neighbors at time ''t'' − 1 then the cellular automaton is properly called ''outer totalistic''.Conway's Game of Life
The Game of Life, also known as Conway's Game of Life or simply Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial ...
is an example of an outer totalistic cellular automaton with cell values 0 and 1; outer totalistic cellular automata with the same Moore neighborhood structure as Life are sometimes called cellular automata.
Related automata
There are many possible generalizations of the cellular automaton concept. One way is by using something other than a rectangular (cubic, ''etc.'') grid. For example, if a plane is tiled with regular hexagons, those hexagons could be used as cells. In many cases the resulting cellular automata are equivalent to those with rectangular grids with specially designed neighborhoods and rules. Another variation would be to make the grid itself irregular, such as with Penrose tiles.
Also, rules can be probabilistic rather than deterministic. Such cellular automata are called probabilistic cellular automata. A probabilistic rule gives, for each pattern at time ''t'', the probabilities that the central cell will transition to each possible state at time ''t'' + 1. Sometimes a simpler rule is used; for example: "The rule is the Game of Life, but on each time step there is a 0.001% probability that each cell will transition to the opposite color."
The neighborhood or rules could change over time or space. For example, initially the new state of a cell could be determined by the horizontally adjacent cells, but for the next generation the vertical cells would be used.
In cellular automata, the new state of a cell is not affected by the new state of other cells. This could be changed so that, for instance, a 2 by 2 block of cells can be determined by itself and the cells adjacent to itself.
There are '' continuous automata''. These are like totalistic cellular automata, but instead of the rule and states being discrete (''e.g.'' a table, using states ), continuous functions are used, and the states become continuous (usually values in ,1. The state of a location is a finite number of real numbers. Certain cellular automata can yield diffusion in liquid patterns in this way.
Continuous spatial automata have a continuum of locations. The state of a location is a finite number of real numbers. Time is also continuous, and the state evolves according to differential equations. One important example is reaction–diffusion textures, differential equations proposed by
One way is by using something other than a rectangular (cubic, ''etc.'') grid. For example, if a plane is tiled with regular hexagons, those hexagons could be used as cells. In many cases the resulting cellular automata are equivalent to those with rectangular grids with specially designed neighborhoods and rules. Another variation would be to make the grid itself irregular, such as with Penrose tiles.
Also, rules can be probabilistic rather than deterministic. Such cellular automata are called probabilistic cellular automata. A probabilistic rule gives, for each pattern at time ''t'', the probabilities that the central cell will transition to each possible state at time ''t'' + 1. Sometimes a simpler rule is used; for example: "The rule is the Game of Life, but on each time step there is a 0.001% probability that each cell will transition to the opposite color."
The neighborhood or rules could change over time or space. For example, initially the new state of a cell could be determined by the horizontally adjacent cells, but for the next generation the vertical cells would be used.
In cellular automata, the new state of a cell is not affected by the new state of other cells. This could be changed so that, for instance, a 2 by 2 block of cells can be determined by itself and the cells adjacent to itself.
There are '' continuous automata''. These are like totalistic cellular automata, but instead of the rule and states being discrete (''e.g.'' a table, using states ), continuous functions are used, and the states become continuous (usually values in ,1. The state of a location is a finite number of real numbers. Certain cellular automata can yield diffusion in liquid patterns in this way.
Continuous spatial automata have a continuum of locations. The state of a location is a finite number of real numbers. Time is also continuous, and the state evolves according to differential equations. One important example is reaction–diffusion textures, differential equations proposed by Alan Turing
Alan Mathison Turing (; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist. He was highly influential in the development of theoretical computer ...
to explain how chemical reactions could create the stripes on zebra
Zebras (, ) (subgenus ''Hippotigris'') are African equines with distinctive black-and-white striped coats. There are three living species: Grévy's zebra (''Equus grevyi''), the plains zebra (''E. quagga''), and the mountain zebra (''E. ...
s and spots on leopards. When these are approximated by cellular automata, they often yield similar patterns. MacLennaconsiders continuous spatial automata as a model of computation. There are known examples of continuous spatial automata, which exhibit propagating phenomena analogous to gliders in the Game of Life. ''Graph rewriting automata'' are extensions of cellular automata based on graph rewriting systems.
Elementary cellular automata
The simplest nontrivial cellular automaton would be one-dimensional, with two possible states per cell, and a cell's neighbors defined as the adjacent cells on either side of it. A cell and its two neighbors form a neighborhood of 3 cells, so there are 23 = 8 possible patterns for a neighborhood. A rule consists of deciding, for each pattern, whether the cell will be a 1 or a 0 in the next generation. There are then 28 = 256 possible rules. These 256 cellular automata are generally referred to by their Wolfram code, a standard naming convention invented by Wolfram that gives each rule a number from 0 to 255. A number of papers have analyzed and compared the distinct cases among the 256 cellular automata (many are trivially isomorphic). The rule 30, rule 90, rule 110, and rule 184 cellular automata are particularly interesting. The images below show the history of rules 30 and 110 when the starting configuration consists of a 1 (at the top of each image) surrounded by 0s. Each row of pixels represents a generation in the history of the automaton, with ''t''=0 being the top row. Each pixel is colored white for 0 and black for 1.
These 256 cellular automata are generally referred to by their Wolfram code, a standard naming convention invented by Wolfram that gives each rule a number from 0 to 255. A number of papers have analyzed and compared the distinct cases among the 256 cellular automata (many are trivially isomorphic). The rule 30, rule 90, rule 110, and rule 184 cellular automata are particularly interesting. The images below show the history of rules 30 and 110 when the starting configuration consists of a 1 (at the top of each image) surrounded by 0s. Each row of pixels represents a generation in the history of the automaton, with ''t''=0 being the top row. Each pixel is colored white for 0 and black for 1.
 Rule 30 exhibits ''class 3'' behavior, meaning even simple input patterns such as that shown lead to chaotic, seemingly random histories.
Rule 110, like the Game of Life, exhibits what Wolfram calls ''class 4'' behavior, which is neither completely random nor completely repetitive. Localized structures appear and interact in various complicated-looking ways. In the course of the development of '' A New Kind of Science'', as a research assistant to Wolfram in 1994, Matthew Cook proved that some of these structures were rich enough to support universality. This result is interesting because rule 110 is an extremely simple one-dimensional system, and difficult to engineer to perform specific behavior. This result therefore provides significant support for Wolfram's view that class 4 systems are inherently likely to be universal. Cook presented his proof at a
Rule 30 exhibits ''class 3'' behavior, meaning even simple input patterns such as that shown lead to chaotic, seemingly random histories.
Rule 110, like the Game of Life, exhibits what Wolfram calls ''class 4'' behavior, which is neither completely random nor completely repetitive. Localized structures appear and interact in various complicated-looking ways. In the course of the development of '' A New Kind of Science'', as a research assistant to Wolfram in 1994, Matthew Cook proved that some of these structures were rich enough to support universality. This result is interesting because rule 110 is an extremely simple one-dimensional system, and difficult to engineer to perform specific behavior. This result therefore provides significant support for Wolfram's view that class 4 systems are inherently likely to be universal. Cook presented his proof at a Santa Fe Institute
The Santa Fe Institute (SFI) is an independent, nonprofit theoretical research institute located in Santa Fe, New Mexico, United States and dedicated to the multidisciplinary study of the fundamental principles of complex adaptive systems, inc ...
conference on Cellular Automata in 1998, but Wolfram blocked the proof from being included in the conference proceedings, as Wolfram did not want the proof announced before the publication of ''A New Kind of Science''. In 2004, Cook's proof was finally published in Wolfram's journal ''Complex Systems
A complex system is a system composed of many components that may interact with one another. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication s ...
'' (Vol. 15, No. 1), over ten years after Cook came up with it. Rule 110 has been the basis for some of the smallest universal Turing machines.
Rule space
An elementary cellular automaton rule is specified by 8 bits, and all elementary cellular automaton rules can be considered to sit on the vertices of the 8-dimensional unithypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
. This unit hypercube is the cellular automaton rule space. For next-nearest-neighbor cellular automata, a rule is specified by 25 = 32 bits, and the cellular automaton rule space is a 32-dimensional unit hypercube. A distance between two rules can be defined by the number of steps required to move from one vertex, which represents the first rule, and another vertex, representing another rule, along the edge of the hypercube. This rule-to-rule distance is also called the Hamming distance
In information theory, the Hamming distance between two String (computer science), strings or vectors of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number ...
.
Cellular automaton rule space allows us to ask the question concerning whether rules with similar dynamical behavior are "close" to each other. Graphically drawing a high dimensional hypercube on the 2-dimensional plane remains a difficult task, and one crude locator of a rule in the hypercube is the number of bit-1 in the 8-bit string for elementary rules (or 32-bit string for the next-nearest-neighbor rules). Drawing the rules in different Wolfram classes in these slices of the rule space show that class 1 rules tend to have lower number of bit-1s, thus located in one region of the space, whereas class 3 rules tend to have higher proportion (50%) of bit-1s.
For larger cellular automaton rule space, it is shown that class 4 rules are located between the class 1 and class 3 rules. This observation is the foundation for the phrase edge of chaos, and is reminiscent of the phase transition
In physics, chemistry, and other related fields like biology, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic Sta ...
in thermodynamics
Thermodynamics is a branch of physics that deals with heat, Work (thermodynamics), work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed b ...
.
Applications
Biology
seashell
A seashell or sea shell, also known simply as a shell, is a hard, protective outer layer usually created by an animal or organism that lives in the sea. Most seashells are made by Mollusca, mollusks, such as snails, clams, and oysters ...
s, like the ones in the genera ''Conus
''Conus'' is a genus of venomous and predatory cone snails.Bouchet, P.; Gofas, S. (2015). Conus Linnaeus, 1758. In: MolluscaBase (2015). Accessed through: World Register of Marine Species at http://www.marinespecies.org/aphia.php?p=taxdetails&i ...
'' and '' Cymbiola'', are generated by natural cellular automata. The pigment
A pigment is a powder used to add or alter color or change visual appearance. Pigments are completely or nearly solubility, insoluble and reactivity (chemistry), chemically unreactive in water or another medium; in contrast, dyes are colored sub ...
cells reside in a narrow band along the shell's lip. Each cell secretes pigments according to the activating and inhibiting activity of its neighbor pigment cells, obeying a natural version of a mathematical rule. The cell band leaves the colored pattern on the shell as it grows slowly. For example, the widespread species '' Conus textile'' bears a pattern resembling Wolfram's rule 30 cellular automaton.
* Plants regulate their intake and loss of gases via a cellular automaton mechanism. Each stoma
In botany, a stoma (: stomata, from Greek language, Greek ''στόμα'', "mouth"), also called a stomate (: stomates), is a pore found in the Epidermis (botany), epidermis of leaves, stems, and other organs, that controls the rate of gas exc ...
on the leaf acts as a cell.
* Moving wave patterns on the skin of cephalopod
A cephalopod is any member of the molluscan Taxonomic rank, class Cephalopoda (Greek language, Greek plural , ; "head-feet") such as a squid, octopus, cuttlefish, or nautilus. These exclusively marine animals are characterized by bilateral symm ...
s can be simulated with a two-state, two-dimensional cellular automata, each state corresponding to either an expanded or retracted chromatophore
Chromatophores are cells that produce color, of which many types are pigment-containing cells, or groups of cells, found in a wide range of animals including amphibians, fish, reptiles, crustaceans and cephalopod
A cephalopod is any member o ...
.
* Threshold automata have been invented to simulate neuron
A neuron (American English), neurone (British English), or nerve cell, is an membrane potential#Cell excitability, excitable cell (biology), cell that fires electric signals called action potentials across a neural network (biology), neural net ...
s, and complex behaviors such as recognition and learning can be simulated.
* Fibroblast
A fibroblast is a type of cell (biology), biological cell typically with a spindle shape that synthesizes the extracellular matrix and collagen, produces the structural framework (Stroma (tissue), stroma) for animal Tissue (biology), tissues, and ...
s bear similarities to cellular automata, as each fibroblast only interacts with its neighbors.
Additionally, biological phenomena which require explicit modeling of the agents' velocities (for example, those involved in collective cell migration) may be modeled by cellular automata with a more complex state space and rules, such as biological lattice-gas cellular automata. These include phenomena of great medical importance, such as:
* Characterization of different modes of metastatic invasion.
* The role of heterogeneity in the development of aggressive carcinomas.
* Phenotypic switching during tumor proliferation.
Chemistry
The Belousov–Zhabotinsky reaction is a spatio-temporal chemical oscillator that can be simulated by means of a cellular automaton. In the 1950s A. M. Zhabotinsky (extending the work of B. P. Belousov) discovered that when a thin, homogenous layer of a mixture of malonic acid, acidified bromate, and a ceric salt were mixed together and left undisturbed, fascinating geometric patterns such as concentric circles and spirals propagate across the medium. In the "Computer Recreations" section of the August 1988 issue of ''Scientific American
''Scientific American'', informally abbreviated ''SciAm'' or sometimes ''SA'', is an American popular science magazine. Many scientists, including Albert Einstein and Nikola Tesla, have contributed articles to it, with more than 150 Nobel Pri ...
'', A. K. Dewdney discussed a cellular automaton developed by Martin Gerhardt and Heike Schuster of the University of Bielefeld (Germany). This automaton produces wave patterns that resemble those in the Belousov-Zhabotinsky reaction. Combining the attachment to one only particle from the growing aggregate, following the seminal model of Witten and Sander to simulate the diffusion-limited growth with the attachment to kink positions as proposed yet by Kossel and Stranski in 1920's, see for the kinetics-limited version of the attachment, Goranova et al proposed a model for electrochemical co-deposition of two metal cations.
Physics
 Probabilistic cellular automata are used in
Probabilistic cellular automata are used in statistical
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
and condensed matter physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid State of matter, phases, that arise from electromagnetic forces between atoms and elec ...
to study phenomena like fluid dynamics and phase transitions. The Ising model
The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical models in physics, mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that r ...
is a prototypical example, in which each cell can be in either of two states called "up" and "down", making an idealized representation of a magnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, steel, nickel, ...
. By adjusting the parameters of the model, the proportion of cells being in the same state can be varied, in ways that help explicate how ferromagnet
Ferromagnetism is a property of certain materials (such as iron) that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromag ...
s become demagnetized when heated. Moreover, results from studying the demagnetization phase transition can be transferred to other phase transitions, like the evaporation of a liquid into a gas; this convenient cross-applicability is known as universality. The phase transition in the two-dimensional Ising model and other systems in its universality class has been of particular interest, as it requires conformal field theory
A conformal field theory (CFT) is a quantum field theory that is invariant under conformal transformations. In two dimensions, there is an infinite-dimensional algebra of local conformal transformations, and conformal field theories can sometime ...
to understand in depth. Other cellular automata that have been of significance in physics include lattice gas automata, which simulate fluid flows. In a series of works the so-called ''vicinal Cellular Automaton'' (vicCA) was proposed and further developed to model the possibly unstable growth and sublimation of vicinal crystal surfaces in 1+1D. Besides the attachment/detachment events being encoded in the rules of the CA, the adatoms on top of the vicinal form a thin layer, and their thermal motion is modeled by a Monte Carlo module. A decisive step further was the transition of the model to 2+1D, where a number of different structures were obtained, referred to by the authors as “vicinal creatures”—step bunches, step meanders, nano-pillars, nanowires, etc. The vicCA model was extensively used by Alexey Redkov to develop a Machine Learning algorithm on top of it, significantly speeding up calculations by a factor of 10⁵ while enabling systematic classification of the observed phenomena.
Computer science, coding, and communication
Cellular automaton processors are physical implementations of CA concepts, which can process information computationally. Processing elements are arranged in a regular grid of identical cells. The grid is usually a square tiling, ortessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety ...
, of two or three dimensions; other tilings are possible, but not yet used. Cell states are determined only by interactions with adjacent neighbor cells. No means exists to communicate directly with cells farther away. One such cellular automaton processor array configuration is the systolic array. Cell interaction can be via electric charge, magnetism, vibration (phonons
A phonon is a collective excitation in a periodic, Elasticity (physics), elastic arrangement of atoms or molecules in condensed matter physics, condensed matter, specifically in solids and some liquids. In the context of optically trapped objects ...
at quantum scales), or any other physically useful means. This can be done in several ways so that no wires are needed between any elements. This is very unlike processors used in most computers today ( von Neumann designs) which are divided into sections with elements that can communicate with distant elements over wires.
Rule 30 was originally suggested as a possible block cipher
In cryptography, a block cipher is a deterministic algorithm that operates on fixed-length groups of bits, called ''blocks''. Block ciphers are the elementary building blocks of many cryptographic protocols. They are ubiquitous in the storage a ...
for use in cryptography
Cryptography, or cryptology (from "hidden, secret"; and ''graphein'', "to write", or ''-logy, -logia'', "study", respectively), is the practice and study of techniques for secure communication in the presence of Adversary (cryptography), ...
. Two-dimensional cellular automata can be used for constructing a pseudorandom number generator
A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG), is an algorithm for generating a sequence of numbers whose properties approximate the properties of sequences of random number generation, random n ...
.
Cellular automata have been proposed for public-key cryptography
Public-key cryptography, or asymmetric cryptography, is the field of cryptographic systems that use pairs of related keys. Each key pair consists of a public key and a corresponding private key. Key pairs are generated with cryptographic alg ...
. The one-way function
In computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here, "easy" and "hard" are to be understood in the sense of computational complexity theory, s ...
is the evolution of a finite CA whose inverse is believed to be hard to find. Given the rule, anyone can easily calculate future states, but it appears to be very difficult to calculate previous states. Cellular automata have also been applied to design error correction codes.
Other problems that can be solved with cellular automata include:
* Firing squad synchronization problem
* Majority problem
Generative art and music
Cellular automata have been used ingenerative music
Generative music is a term popularized by Brian Eno to describe music that is ever-different and changing, and that is created by a system.
Historical background
In 1995 whilst working with SSEYO's Koan_(program), Koan software (built by Tim ...
and evolutionary music composition and procedural terrain generation in video games.
Maze generation
Specific rules
Specific cellular automata rules include: * Brian's Brain *Codd's cellular automaton
Codd's cellular automaton is a cellular automaton (CA) devised by the United Kingdom, British computer scientist Edgar F. Codd in 1968. It was designed to recreate the computation- and construction-universality of von Neumann cellular automaton, ...
* CoDi
* Conway's game of life
The Game of Life, also known as Conway's Game of Life or simply Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial ...
* Day and Night
* Langton's ant
* Langton's loops
Langton's loops are a particular "species" of artificial life in a cellular automaton created in 1984 by Christopher Langton. They consist of a loop of cells containing genetic information, which flows continuously around the loop and out alon ...
* Lenia
* Nobili cellular automata
* Rule 90
* Rule 184
* Seeds
* Turmite
* Von Neumann cellular automaton
Von Neumann cellular automata are the original expression of cellular automata, the development of which was prompted by suggestions made to John von Neumann by his close friend and fellow mathematician Stanislaw Ulam. Their original purpose w ...
* Wireworld
See also
* * * * * * * * * * * *References
Works cited
* * * * * * * * * *Further reading
* * * * * Proposes reaction-diffusion, a type of continuous automaton.External links
Mirek's Cellebration
– Home to free cellular automata explorer software, "MCell". The software supports a large number of 1D and 2D rules. The site provides both an extensive rules lexicon and many image galleries loaded with examples of rules. Source code (Javascript) is available.
Golly
supports von Neumann, Nobili, GOL, and a great many other systems of cellular automata. Developed by Tomas Rokicki and Andrew Trevorrow. This is the only simulator currently available that can demonstrate von Neumann type self-replication.
– An atlas of various types of one-dimensional cellular automata.
Conway Life
from the newsgroup comp.theory.cell-automata
(includes discussion on triangular grids, and larger neighborhood CAs)
contains an extensive list of academic and professional reference material. {{Authority control Systems theory Dynamical systems Computational fields of study