symmetry on:
[Wikipedia]
[Google]
[Amazon]


 Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including
 A geometric shape or object is symmetric if it can be divided into two or more identical pieces that are arranged in an organized fashion. This means that an object is symmetric if there is a transformation that moves individual pieces of the object, but doesn't change the overall shape. The type of symmetry is determined by the way the pieces are organized, or by the type of transformation:
* An object has
A geometric shape or object is symmetric if it can be divided into two or more identical pieces that are arranged in an organized fashion. This means that an object is symmetric if there is a transformation that moves individual pieces of the object, but doesn't change the overall shape. The type of symmetry is determined by the way the pieces are organized, or by the type of transformation:
* An object has

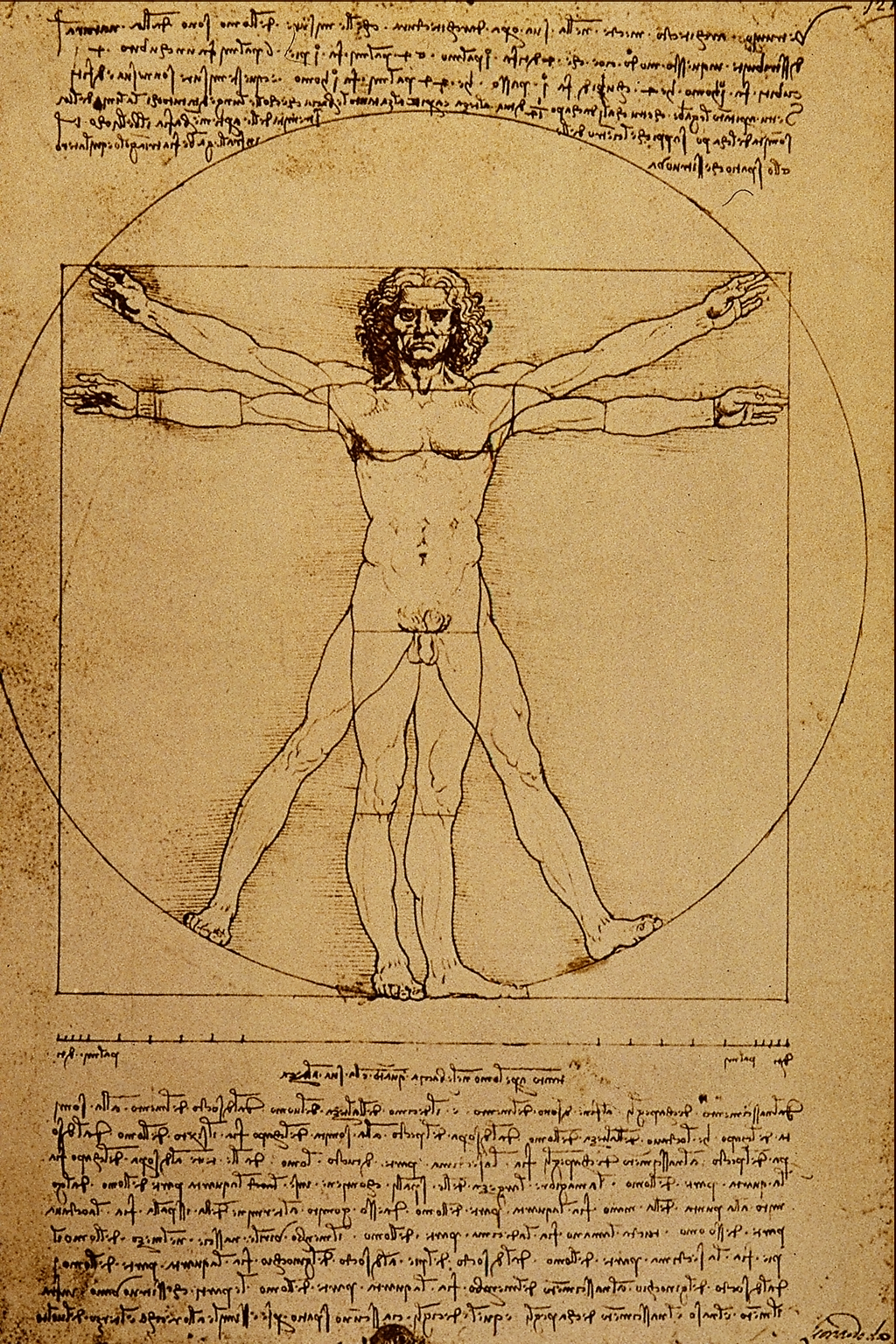 In biology, the notion of symmetry is mostly used explicitly to describe body shapes. Bilateral animals, including humans, are more or less symmetric with respect to the
In biology, the notion of symmetry is mostly used explicitly to describe body shapes. Bilateral animals, including humans, are more or less symmetric with respect to the
 There exists a list of journals and newsletters known to deal, at least in part, with symmetry and the arts.
There exists a list of journals and newsletters known to deal, at least in part, with symmetry and the arts.

 Symmetry finds its ways into architecture at every scale, from the overall external views of buildings such as Gothic
Symmetry finds its ways into architecture at every scale, from the overall external views of buildings such as Gothic
 Since the earliest uses of
Since the earliest uses of
 A long tradition of the use of symmetry in
A long tradition of the use of symmetry in
 As
As
 Symmetries appear in the design of objects of all kinds. Examples include
Symmetries appear in the design of objects of all kinds. Examples include
File:Major and minor triads, triangles.png, Major and minor triads on the white piano keys are symmetrical to the D. (compare article) (file)
poly 35 442 35 544 179 493 root of A minor triad
poly 479 462 446 493 479 526 513 492 third of A minor triad
poly 841 472 782 493 840 514 821 494 fifth of A minor triad
poly 926 442 875 460 906 493 873 525 926 545 fifth of A minor triad
poly 417 442 417 544 468 525 437 493 469 459 root of C major triad
poly 502 472 522 493 502 514 560 493 root of C major triad
poly 863 462 830 493 863 525 895 493 third of C major triad
poly 1303 442 1160 493 1304 544 fifth of C major triad
poly 280 406 264 413 282 419 275 413 fifth of E minor triad
poly 308 397 293 403 301 412 294 423 309 428 fifth of E minor triad
poly 844 397 844 428 886 413 root of E minor triad
poly 1240 404 1230 412 1239 422 1250 412 third of E minor triad
poly 289 404 279 413 288 422 300 413 third of G major triad
poly 689 398 646 413 689 429 fifth of G major triad
poly 1221 397 1222 429 1237 423 1228 414 1237 403 root of G major triad
poly 1249 406 1254 413 1249 418 1265 413 root of G major triad
poly 89 567 73 573 90 579 86 573 fifth of D minor triad
poly 117 558 102 563 111 572 102 583 118 589 fifth of D minor triad
poly 650 558 650 589 693 573 root of D minor triad
poly 1050 563 1040 574 1050 582 1061 574 third of D minor triad
poly 98 565 88 573 98 583 110 574 third of F major triad
poly 498 558 455 573 498 589 fifth of F major triad
poly 1031 557 1031 589 1047 583 1038 574 1046 563 root of F major triad
poly 1075 573 1059 580 1064 573 1058 567 root of F major triad
desc none
Symmetry is not restricted to the visual arts. Its role in the history of
International Symmetry Association (ISA)Dutch: Symmetry Around a Point in the Plane
Symmetry
BBC Radio 4 discussion with Fay Dowker, Marcus du Sautoy & Ian Stewart (''In Our Time'', Apr. 19, 2007) {{Patterns in nature Geometry Theoretical physics Artistic techniques Aesthetics
 Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. The English language draws a terminological distinction (which does not exist in every language) between ''transla ...
, reflection Reflection or reflexion may refer to:
Science and technology
* Reflection (physics), a common wave phenomenon
** Specular reflection, reflection from a smooth surface
*** Mirror image, a reflection in a mirror or in water
** Signal reflection, in ...
, rotation or scaling
Scaling may refer to:
Science and technology
Mathematics and physics
* Scaling (geometry), a linear transformation that enlarges or diminishes objects
* Scale invariance, a feature of objects or laws that do not change if scales of length, energ ...
. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article.
Mathematical symmetry may be observed with respect to the passage of time
Time is the continued sequence of existence and events that occurs in an apparently irreversible succession from the past, through the present, into the future. It is a component quantity of various measurements used to sequence events, ...
; as a spatial relationship; through geometric transformation
In mathematics, a geometric transformation is any bijection of a set to itself (or to another such set) with some salient geometrical underpinning. More specifically, it is a function whose domain and range are sets of points — most often b ...
s; through other kinds of functional transformations; and as an aspect of abstract objects, including theoretic models, language
Language is a structured system of communication. The structure of a language is its grammar and the free components are its vocabulary. Languages are the primary means by which humans communicate, and may be conveyed through a variety of ...
, and music
Music is generally defined as the art of arranging sound to create some combination of form, harmony, melody, rhythm or otherwise expressive content. Exact definitions of music vary considerably around the world, though it is an aspe ...
.
This article describes symmetry from three perspectives: in mathematics, including geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ...
, the most familiar type of symmetry for many people; in science
Science is a systematic endeavor that Scientific method, builds and organizes knowledge in the form of Testability, testable explanations and predictions about the universe.
Science may be as old as the human species, and some of the earli ...
and nature
Nature, in the broadest sense, is the physical world or universe. "Nature" can refer to the phenomena of the physical world, and also to life in general. The study of nature is a large, if not the only, part of science. Although humans are ...
; and in the arts, covering architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and constructing building ...
, art
Art is a diverse range of human activity, and resulting product, that involves creative or imaginative talent expressive of technical proficiency, beauty, emotional power, or conceptual ideas.
There is no generally agreed definition of wha ...
and music
Music is generally defined as the art of arranging sound to create some combination of form, harmony, melody, rhythm or otherwise expressive content. Exact definitions of music vary considerably around the world, though it is an aspe ...
.
The opposite of symmetry is asymmetry, which refers to the absence or a violation of symmetry.
In mathematics
In geometry
reflectional symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.
In 2D ther ...
(line or mirror symmetry) if there is a line (or in 3D a plane) going through it which divides it into two pieces that are mirror images of each other.
*An object has rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which i ...
if the object can be rotated about a fixed point (or in 3D about a line) without changing the overall shape.
*An object has translational symmetry
In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by .
In physics and mathematics, continuous translational symmetry is the invariance of a system of equati ...
if it can be translated
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. The English language draws a terminological distinction (which does not exist in every language) between ''transla ...
(moving every point of the object by the same distance) without changing its overall shape.
*An object has helical symmetry if it can be simultaneously translated and rotated in three-dimensional space along a line known as a screw axis
A screw axis (helical axis or twist axis) is a line that is simultaneously the axis of rotation and the line along which translation of a body occurs. Chasles' theorem shows that each Euclidean displacement in three-dimensional space has a scre ...
.
*An object has scale symmetry
In physics, mathematics and statistics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor, and thus represent a universality.
The technical te ...
if it does not change shape when it is expanded or contracted. Fractals
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illus ...
also exhibit a form of scale symmetry, where smaller portions of the fractal are similar in shape to larger portions.
*Other symmetries include glide reflection
In 2-dimensional geometry, a glide reflection (or transflection) is a symmetry operation that consists of a reflection over a line and then translation along that line, combined into a single operation. The intermediate step between reflection ...
symmetry (a reflection followed by a translation) and rotoreflection
In geometry, an improper rotation,. also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicul ...
symmetry (a combination of a rotation and a reflection).
In logic
Adyadic relation
In mathematics, a binary relation associates elements of one set, called the ''domain'', with elements of another set, called the ''codomain''. A binary relation over Set (mathematics), sets and is a new set of ordered pairs consisting of ele ...
''R'' = ''S'' × ''S'' is symmetric if for all elements ''a'', ''b'' in ''S'', whenever it is true that ''Rab'', it is also true that ''Rba''. Thus, the relation "is the same age as" is symmetric, for if Paul is the same age as Mary, then Mary is the same age as Paul.
In propositional logic, symmetric binary logical connective
In logic, a logical connective (also called a logical operator, sentential connective, or sentential operator) is a logical constant. They can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary ...
s include ''and
or AND may refer to:
Logic, grammar, and computing
* Conjunction (grammar), connecting two words, phrases, or clauses
* Logical conjunction in mathematical logic, notated as "∧", "⋅", "&", or simple juxtaposition
* Bitwise AND, a boolea ...
'' (∧, or &), '' or'' (∨, or , ) and ''if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is b ...
'' (↔), while the connective ''if'' (→) is not symmetric. Other symmetric logical connectives include '' nand'' (not-and, or ⊼), '' xor'' (not-biconditional, or ⊻), and '' nor'' (not-or, or ⊽).
Other areas of mathematics
Generalizing from geometrical symmetry in the previous section, one can say that amathematical object
A mathematical object is an abstract concept arising in mathematics.
In the usual language of mathematics, an ''object'' is anything that has been (or could be) formally defined, and with which one may do deductive reasoning and mathematical p ...
is ''symmetric'' with respect to a given mathematical operation
In mathematics, an operation is a Function (mathematics), function which takes zero or more input values (also called "''operands''" or "arguments") to a well-defined output value. The number of operands is the arity of the operation.
The most c ...
, if, when applied to the object, this operation preserves some property of the object. The set of operations that preserve a given property of the object form a group
A group is a number of persons or things that are located, gathered, or classed together.
Groups of people
* Cultural group, a group whose members share the same cultural identity
* Ethnic group, a group whose members share the same ethnic ide ...
.
In general, every kind of structure in mathematics will have its own kind of symmetry. Examples include even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power ser ...
in calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
, symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group ...
s in abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures. Algebraic structures include group (mathematics), groups, ring (mathematics), rings, field (mathematics), fields, module (mathe ...
, symmetric matrices
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally,
Because equal matrices have equal dimensions, only square matrices can be symmetric.
The entries of a symmetric matrix are symmetric with re ...
in linear algebra
Linear algebra is the branch of mathematics concerning linear equations such as:
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as:
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrices ...
, and Galois group
In mathematics, in the area of abstract algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension. The study of field extensions and their relationship to the po ...
s in Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory to ...
. In statistics, symmetry also manifests as symmetric probability distributions, and as skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
For a unimodal ...
—the asymmetry of distributions.
In science and nature
In physics
Symmetry in physics has been generalized to mean invariance—that is, lack of change—under any kind of transformation, for example arbitrary coordinate transformations. This concept has become one of the most powerful tools oftheoretical physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experim ...
, as it has become evident that practically all laws of nature originate in symmetries. In fact, this role inspired the Nobel laureate PW Anderson to write in his widely read 1972 article ''More is Different'' that "it is only slightly overstating the case to say that physics is the study of symmetry." See Noether's theorem
Noether's theorem or Noether's first theorem states that every differentiable symmetry of the action of a physical system with conservative forces has a corresponding conservation law. The theorem was proven by mathematician Emmy Noether ...
(which, in greatly simplified form, states that for every continuous mathematical symmetry, there is a corresponding conserved quantity such as energy or momentum; a conserved current, in Noether's original language); and also, Wigner's classification
In mathematics and theoretical physics, Wigner's classification
is a classification of the nonnegative ~ (~E \ge 0~)~ energy irreducible unitary representations of the Poincaré group which have either finite or zero mass eigenvalues. (Since thi ...
, which says that the symmetries of the laws of physics determine the properties of the particles found in nature.
Important symmetries in physics include continuous symmetries and discrete symmetries of spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differ ...
; internal symmetries of particles; and supersymmetry of physical theories.
In biology

 In biology, the notion of symmetry is mostly used explicitly to describe body shapes. Bilateral animals, including humans, are more or less symmetric with respect to the
In biology, the notion of symmetry is mostly used explicitly to describe body shapes. Bilateral animals, including humans, are more or less symmetric with respect to the sagittal plane
The sagittal plane (; also known as the longitudinal plane) is an anatomical plane that divides the body into right and left sections. It is perpendicular to the transverse and coronal planes. The plane may be in the center of the body and div ...
which divides the body into left and right halves. Animals that move in one direction necessarily have upper and lower sides, head and tail ends, and therefore a left and a right. The head becomes specialized with a mouth and sense organs, and the body becomes bilaterally symmetric for the purpose of movement, with symmetrical pairs of muscles and skeletal elements, though internal organs often remain asymmetric.
Plants and sessile (attached) animals such as sea anemones often have radial or rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which i ...
, which suits them because food or threats may arrive from any direction. Fivefold symmetry is found in the echinoderms, the group that includes starfish, sea urchins, and sea lilies.
In biology, the notion of symmetry is also used as in physics, that is to say to describe the properties of the objects studied, including their interactions. A remarkable property of biological evolution is the changes of symmetry corresponding to the appearance of new parts and dynamics.
In chemistry
Symmetry is important to chemistry because it undergirds essentially all ''specific'' interactions between molecules in nature (i.e., via the interaction of natural and human-madechiral
Chirality is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is distinguishable from i ...
molecules with inherently chiral biological systems). The control of the symmetry of molecules produced in modern chemical synthesis
As a topic of chemistry, chemical synthesis (or combination) is the artificial execution of chemical reactions to obtain one or several products. This occurs by physical and chemical manipulations usually involving one or more reactions. In mod ...
contributes to the ability of scientists to offer therapeutic
A therapy or medical treatment (often abbreviated tx, Tx, or Tx) is the attempted remediation of a health problem, usually following a medical diagnosis.
As a rule, each therapy has indications and contraindications. There are many different ...
interventions with minimal side effects
In medicine, a side effect is an effect, whether therapeutic or adverse, that is secondary to the one intended; although the term is predominantly employed to describe adverse effects, it can also apply to beneficial, but unintended, consequence ...
. A rigorous understanding of symmetry explains fundamental observations in quantum chemistry, and in the applied areas of spectroscopy and crystallography. The theory and application of symmetry to these areas of physical science
Physical science is a branch of natural science that studies non-living systems, in contrast to life science. It in turn has many branches, each referred to as a "physical science", together called the "physical sciences".
Definition
Phy ...
draws heavily on the mathematical area of group theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field ...
.
In psychology and neuroscience
For a human observer, some symmetry types are more salient than others, in particular the most salient is a reflection with a vertical axis, like that present in the human face. Ernst Mach made this observation in his book "The analysis of sensations" (1897), and this implies that perception of symmetry is not a general response to all types of regularities. Both behavioural and neurophysiological studies have confirmed the special sensitivity to reflection symmetry in humans and also in other animals. Early studies within theGestalt
Gestalt may refer to:
Psychology
* Gestalt psychology, a school of psychology
* Gestalt therapy, a form of psychotherapy
* Bender Visual-Motor Gestalt Test, an assessment of development disorders
* Gestalt Practice, a practice of self-exploration ...
tradition suggested that bilateral symmetry was one of the key factors in perceptual grouping
Grouping may refer to:
* Muenchian grouping
* Principles of grouping
* Railways Act 1921, also known as Grouping Act, a reorganisation of the British railway system
* Grouping (firearms), the pattern of multiple shots from a sidearm
See also ...
. This is known as the Law of Symmetry. The role of symmetry in grouping and figure/ground organization has been confirmed in many studies. For instance, detection of reflectional symmetry is faster when this is a property of a single object. Studies of human perception and psychophysics have shown that detection of symmetry is fast, efficient and robust to perturbations. For example, symmetry can be detected with presentations between 100 and 150 milliseconds.
More recent neuroimaging studies have documented which brain regions are active during perception of symmetry. Sasaki et al. used functional magnetic resonance imaging (fMRI) to compare responses for patterns with symmetrical or random dots. A strong activity was present in extrastriate regions of the occipital cortex but not in the primary visual cortex. The extrastriate regions included V3A, V4, V7, and the lateral occipital complex (LOC). Electrophysiological studies have found a late posterior negativity that originates from the same areas. In general, a large part of the visual system seems to be involved in processing visual symmetry, and these areas involve similar networks to those responsible for detecting and recognising objects.
In social interactions
People observe the symmetrical nature, often including asymmetrical balance, of social interactions in a variety of contexts. These include assessments of reciprocity,empathy
Empathy is the capacity to understand or feel what another person is experiencing from within their frame of reference, that is, the capacity to place oneself in another's position. Definitions of empathy encompass a broad range of social, co ...
, sympathy
Sympathy is the perception of, understanding of, and reaction to the distress or need of another life form. According to David Hume, this sympathetic concern is driven by a switch in viewpoint from a personal perspective to the perspective of an ...
, apology, dialogue, respect, justice
Justice, in its broadest sense, is the principle that people receive that which they deserve, with the interpretation of what then constitutes "deserving" being impacted upon by numerous fields, with many differing viewpoints and perspective ...
, and revenge.
Reflective equilibrium
Reflective equilibrium is a state of balance or coherence among a set of beliefs arrived at by a process of deliberative mutual adjustment among general principles and particular judgements. Although he did not use the term, philosopher Nelson G ...
is the balance that may be attained through deliberative mutual adjustment among general principles and specific judgment
Judgement (or US spelling judgment) is also known as ''adjudication'', which means the evaluation of evidence to make a decision. Judgement is also the ability to make considered decisions. The term has at least five distinct uses. Aristotle s ...
s.
Symmetrical interactions send the moral message "we are all the same" while asymmetrical interactions may send the message "I am special; better than you." Peer relationships, such as can be governed by the golden rule, are based on symmetry, whereas power relationships are based on asymmetry. Symmetrical relationships can to some degree be maintained by simple ( game theory) strategies seen in symmetric games such as tit for tat
Tit for tat is an English saying meaning "equivalent retaliation". It developed from "tip for tap", first recorded in 1558.
It is also a highly effective strategy in game theory. An intelligent agent, agent using this strategy will first coope ...
.
In the arts
 There exists a list of journals and newsletters known to deal, at least in part, with symmetry and the arts.
There exists a list of journals and newsletters known to deal, at least in part, with symmetry and the arts.
In architecture

cathedral
A cathedral is a church that contains the '' cathedra'' () of a bishop, thus serving as the central church of a diocese, conference, or episcopate. Churches with the function of "cathedral" are usually specific to those Christian denominatio ...
s and The White House
The White House is the official residence and workplace of the president of the United States. It is located at 1600 Pennsylvania Avenue NW in Washington, D.C., and has been the residence of every U.S. president since John Adams in 180 ...
, through the layout of the individual floor plan
In architecture and building engineering, a floor plan is a technical drawing to scale, showing a view from above, of the relationships between rooms, spaces, traffic patterns, and other physical features at one level of a structure.
Dimensio ...
s, and down to the design of individual building elements such as tile mosaics. Islamic buildings such as the Taj Mahal
The Taj Mahal (; ) is an Islamic ivory-white marble mausoleum on the right bank of the river Yamuna in the Indian city of Agra. It was commissioned in 1631 by the Mughal emperor Shah Jahan () to house the tomb of his favourite wife, Mu ...
and the Lotfollah mosque make elaborate use of symmetry both in their structure and in their ornamentation. Moorish buildings like the Alhambra are ornamented with complex patterns made using translational and reflection symmetries as well as rotations.
It has been said that only bad architects rely on a "symmetrical layout of blocks, masses and structures"; Modernist architecture
Modern architecture, or modernist architecture, was an architectural movement or architectural style based upon new and innovative technologies of construction, particularly the use of glass, steel, and reinforced concrete; the idea that form ...
, starting with International style, relies instead on "wings and balance of masses".
In pottery and metal vessels
 Since the earliest uses of
Since the earliest uses of pottery wheel
In pottery, a potter's wheel is a machine used in the shaping (known as throwing) of clay into round ceramic ware. The wheel may also be used during the process of trimming excess clay from leather-hard dried ware that is stiff but malleable, ...
s to help shape clay vessels, pottery has had a strong relationship to symmetry. Pottery created using a wheel acquires full rotational symmetry in its cross-section, while allowing substantial freedom of shape in the vertical direction. Upon this inherently symmetrical starting point, potters from ancient times onwards have added patterns that modify the rotational symmetry to achieve visual objectives.
Cast metal vessels lacked the inherent rotational symmetry of wheel-made pottery, but otherwise provided a similar opportunity to decorate their surfaces with patterns pleasing to those who used them. The ancient Chinese
Chinese can refer to:
* Something related to China
* Chinese people, people of Chinese nationality, citizenship, and/or ethnicity
**''Zhonghua minzu'', the supra-ethnic concept of the Chinese nation
** List of ethnic groups in China, people of ...
, for example, used symmetrical patterns in their bronze castings as early as the 17th century BC. Bronze vessels exhibited both a bilateral main motif and a repetitive translated border design.
In carpets and rugs
 A long tradition of the use of symmetry in
A long tradition of the use of symmetry in carpet
A carpet is a textile floor covering typically consisting of an upper layer of pile attached to a backing. The pile was traditionally made from wool, but since the 20th century synthetic fibers such as polypropylene, nylon, or polyester hav ...
and rug patterns spans a variety of cultures. American Navajo Indians used bold diagonals and rectangular motifs. Many Oriental rugs
An oriental rug is a heavy textile made for a wide variety of utilitarian and symbolic purposes and produced in " Oriental countries" for home use, local sale, and export.
Oriental carpets can be pile woven or flat woven without pile, using v ...
have intricate reflected centers and borders that translate a pattern. Not surprisingly, rectangular rugs have typically the symmetries of a rectangle—that is, motifs that are reflected across both the horizontal and vertical axes (see ).
In quilts
quilt
A quilt is a multi-layered textile, traditionally composed of two or more layers of fabric or fiber. Commonly three layers are used with a filler material. These layers traditionally include a woven cloth top, a layer of padding, batting or w ...
s are made from square blocks (usually 9, 16, or 25 pieces to a block) with each smaller piece usually consisting of fabric triangles, the craft lends itself readily to the application of symmetry.
In other arts and crafts
beadwork
Beadwork is the art or craft of attaching beads to one another by stringing them onto a thread or thin wire with a sewing or beading needle or sewing them to cloth. Beads are produced in a diverse range of materials, shapes, and sizes, and vary b ...
, furniture, sand painting
Sandpainting is the art of pouring coloured sands, and powdered pigments from minerals or crystals, or pigments from other natural or synthetic sources onto a surface to make a fixed or unfixed sand painting. Unfixed sand paintings have a long es ...
s, knot
A knot is an intentional complication in cordage which may be practical or decorative, or both. Practical knots are classified by function, including hitches, bends, loop knots, and splices: a ''hitch'' fastens a rope to another object; a ' ...
work, masks
A mask is an object normally worn on the face, typically for protection, disguise, performance, or entertainment and often they have been employed for rituals and rights. Masks have been used since antiquity for both ceremonial and practi ...
, and musical instruments
A musical instrument is a device created or adapted to make musical sounds. In principle, any object that produces sound can be considered a musical instrument—it is through purpose that the object becomes a musical instrument. A person who pl ...
. Symmetries are central to the art of M.C. Escher
Maurits Cornelis Escher (; 17 June 1898 – 27 March 1972) was a Dutch graphic artist who made Mathematics and art, mathematically inspired woodcuts, lithography, lithographs, and mezzotints.
Despite wide popular interest, Escher was for ...
and the many applications of tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety o ...
in art and craft forms such as wallpaper
Wallpaper is a material used in interior decoration to decorate the interior walls of domestic and public buildings. It is usually sold in rolls and is applied onto a wall using wallpaper paste. Wallpapers can come plain as "lining paper" (so ...
, ceramic tilework such as in Islamic geometric decoration, batik
Batik is an Indonesian technique of wax-resist dyeing applied to the whole cloth. This technique originated from the island of Java, Indonesia. Batik is made either by drawing dots and lines of the resist with a spouted tool called a ''ca ...
, ikat
''Ikat'' (in Indonesian languages means "bind") is a dyeing technique originating from Indonesia used to pattern textiles that employs resist dyeing on the yarns prior to dyeing and weaving the fabric.
In ''ikat'', the resist is formed by b ...
, carpet-making, and many kinds of textile
Textile is an umbrella term that includes various fiber-based materials, including fibers, yarns, filaments, threads, different fabric types, etc. At first, the word "textiles" only referred to woven fabrics. However, weaving is not the ...
and embroidery
Embroidery is the craft of decorating fabric or other materials using a needle to apply thread or yarn. Embroidery may also incorporate other materials such as pearls, beads, quills, and sequins. In modern days, embroidery is usually seen ...
patterns.
Symmetry is also used in designing logos. By creating a logo on a grid and using the theory of symmetry, designers can organize their work, create a symmetric or asymmetrical design, determine the space between letters, determine how much negative space is required in the design, and how to accentuate parts of the logo to make it stand out.
In music
music
Music is generally defined as the art of arranging sound to create some combination of form, harmony, melody, rhythm or otherwise expressive content. Exact definitions of music vary considerably around the world, though it is an aspe ...
touches many aspects of the creation and perception of music.
Musical form
Symmetry has been used as a formal constraint by many composers, such as the arch (swell) form (ABCBA) used by Steve Reich, Béla Bartók, andJames Tenney
James Tenney (August 10, 1934 – August 24, 2006) was an American composer and music theorist. He made significant early musical contributions to plunderphonics, sound synthesis, algorithmic composition, process music, spectral music, microto ...
. In classical music, Bach used the symmetry concepts of permutation and invariance.
Pitch structures
Symmetry is also an important consideration in the formation of scales andchords
Chord may refer to:
* Chord (music), an aggregate of musical pitches sounded simultaneously
** Guitar chord a chord played on a guitar, which has a particular tuning
* Chord (geometry), a line segment joining two points on a curve
* Chord ( ...
, traditional or tonal music being made up of non-symmetrical groups of pitches, such as the diatonic scale or the major chord
In music theory
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the " rudiments", that are needed to understan ...
. Symmetrical scale
In music, a symmetric scale is a music scale which equally divides the octave. The concept and term appears to have been introduced by Joseph Schillinger and further developed by Nicolas Slonimsky as part of his famous ''Thesaurus of Scales and M ...
s or chords, such as the whole tone scale
In music, a whole-tone scale is a scale in which each note is separated from its neighbors by the interval of a whole tone. In twelve-tone equal temperament, there are only two complementary whole-tone scales, both six-note or '' hexatonic' ...
, augmented chord, or diminished seventh chord
A seventh chord is a chord consisting of a triad plus a note forming an interval of a seventh above the chord's root. When not otherwise specified, a "seventh chord" usually means a dominant seventh chord: a major triad together with a mi ...
(diminished-diminished seventh), are said to lack direction or a sense of forward motion, are ambiguous as to the key or tonal center, and have a less specific diatonic functionality
In music, function (also referred to as harmonic function) is a term used to denote the relationship of a chord"Function", unsigned article, ''Grove Music Online'', . or a scale degree to a tonal centre. Two main theories of tonal functions exis ...
. However, composers such as Alban Berg, Béla Bartók, and George Perle
George Perle (6 May 1915 – 23 January 2009) was an American composer and music theorist. As a composer, his music was largely atonal, using methods similar to the twelve-tone technique of the Second Viennese School. This serialist style, and ...
have used axes of symmetry and/or interval cycle In music, an interval cycle is a collection of pitch classes created from a sequence of the same interval class.Whittall, Arnold. 2008. ''The Cambridge Introduction to Serialism'', p. 273-74. New York: Cambridge University Press. (pbk). In other ...
s in an analogous way to keys or non- tonal tonal center
Center or centre may refer to:
Mathematics
*Center (geometry), the middle of an object
* Center (algebra), used in various contexts
** Center (group theory)
** Center (ring theory)
* Graph center, the set of all vertices of minimum eccentrici ...
s. George Perle explains "C–E, D–F♯, ndEb–G, are different instances of the same interval … the other kind of identity. … has to do with axes of symmetry. C–E belongs to a family of symmetrically related dyads as follows:"
Thus in addition to being part of the interval-4 family, C–E is also a part of the sum-4 family (with C equal to 0).
Interval cycles are symmetrical and thus non-diatonic. However, a seven pitch segment of C5 (the cycle of fifths, which are enharmonic with the cycle of fourths) will produce the diatonic major scale. Cyclic tonal progressions in the works of Romantic composers such as Gustav Mahler and Richard Wagner form a link with the cyclic pitch successions in the atonal music of Modernists such as Bartók, Alexander Scriabin, Edgard Varèse, and the Vienna school. At the same time, these progressions signal the end of tonality.
The first extended composition consistently based on symmetrical pitch relations was probably Alban Berg's ''Quartet'', Op. 3 (1910).
Equivalency
Tone row
In music, a tone row or note row (german: Reihe or '), also series or set, is a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets ...
s or pitch class
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave positio ...
sets which are invariant under retrograde are horizontally symmetrical, under inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
vertically. See also Asymmetric rhythm
In music, the terms ''additive'' and ''divisive'' are used to distinguish two types of both rhythm and meter:
* A divisive (or, alternately, multiplicative) rhythm is a rhythm in which a larger period of time is divided into smaller rhythmic unit ...
.
In aesthetics
The relationship of symmetry toaesthetics
Aesthetics, or esthetics, is a branch of philosophy that deals with the nature of beauty and taste, as well as the philosophy of art (its own area of philosophy that comes out of aesthetics). It examines aesthetic values, often expressed t ...
is complex. Humans find bilateral symmetry in faces physically attractive; it indicates health and genetic fitness.Jones, B. C., Little, A. C., Tiddeman, B. P., Burt, D. M., & Perrett, D. I. (2001). Facial symmetry and judgements of apparent health Support for a “‘ good genes ’” explanation of the attractiveness – symmetry relationship, 22, 417–429. Opposed to this is the tendency for excessive symmetry to be perceived as boring or uninteresting. Rudolf Arnheim suggested that people prefer shapes that have some symmetry, and enough complexity to make them interesting.
In literature
Symmetry can be found in various forms inliterature
Literature is any collection of written work, but it is also used more narrowly for writings specifically considered to be an art form, especially prose fiction, drama, and poetry. In recent centuries, the definition has expanded to include ...
, a simple example being the palindrome where a brief text reads the same forwards or backwards. Stories may have a symmetrical structure, such as the rise and fall pattern of '' Beowulf''.
See also
* Automorphism * Burnside's lemma * Chirality *Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power ser ...
*Fixed points of isometry groups in Euclidean space A fixed point of an isometry group is a point that is a fixed point for every isometry in the group. For any isometry group in Euclidean space the set of fixed points is either empty or an affine space.
For an object, any unique centre and, more g ...
– center of symmetry
*Isotropy
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe ...
* Palindrome
*Spacetime symmetries
Spacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems. Spacetime symmetries are used in the study of exact ...
*Spontaneous symmetry breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or ...
* Symmetry-breaking constraints
* Symmetric relation
* Symmetries of polyiamonds
* Symmetries of polyominoes
* Symmetry group
*Wallpaper group
A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. To a given wallpaper there corresponds a group of such congruent transformati ...
Notes
References
Further reading
* ''The Equation That Couldn't Be Solved: How Mathematical Genius Discovered the Language of Symmetry'',Mario Livio
Mario Livio (born June 19, 1945) is an Israeli-American astrophysicist and an author of works that popularize science and mathematics. For 24 years (1991-2015) he was an astrophysicist at the Space Telescope Science Institute, which operates th ...
, Souvenir Press
Ernest Hecht (21 September 1929 – 13 February 2018)Katherine Cowdrey"'Wise and witty' Ernest Hecht dies, aged 88" ''The Bookseller'', 13 February 2018. was a British publisher, producer, and philanthropist. In 1951, he founded Souvenir Press L ...
2006,
External links
International Symmetry Association (ISA)
Symmetry
BBC Radio 4 discussion with Fay Dowker, Marcus du Sautoy & Ian Stewart (''In Our Time'', Apr. 19, 2007) {{Patterns in nature Geometry Theoretical physics Artistic techniques Aesthetics