Rhombicosidodecahedron

In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.

It has a total of 62 faces: 20 regular triangular faces, 30 square faces, 12 regular pentagonal faces, with 60 vertices, and 120 edges.

Names

Johannes Kepler in ''Harmonices Mundi'' (1618) named this polyhedron a ''rhombicosidodecahedron'', being short for ''truncated icosidodecahedral rhombus'', with ''icosidodecahedral rhombus'' being his name for a rhombic triacontahedron. There are different truncations of a rhombic triacontahedron into a topological rhombicosidodecahedron: Prominently its rectification (left), the one that creates the uniform solid (center), and the rectification of the dual icosidodecahedron (right), which is the core of the dual compound.

Dimensions

For a rhombicosidodecahedron with edge length ''a'', its surface area and volume are:

:$\begin A &= \left(30+5\sqrt+3\sqrt\right)a^2 &&\approx 59.305\,982\,844\,9 a^2 \\ V &=\fraca^3 &&\approx 41.615\,323\,782\,5 a^3 \end$

Geometric relations

Expanding an icosidodecahedron by moving the faces away from the origin the right amount, rotating each face so that each triangle vertex continues to touch a pentagon vertex, without changing the size of the faces, and patching the square holes in the result, yields a rhombicosidodecahedron. Therefore, it has the same number of triangles as an icosahedron and the same number of pentagons as a dodecahedron, with a square for each edge of either.

Alternatively, expanding each of five cubes by moving the faces away from the origin the right amount and rotating each of the five 72° around so they are equidistant from each other, without changing the orientation or size of the faces, and patching the pentagonal and triangular holes in the result, yields a rhombicosidodecahedron. Therefore, it has the same number of squares as five cubes.

Two clusters of faces of the bilunabirotunda, the ''lunes'' (each ''lune'' featuring two triangles adjacent to opposite sides of one square), can be aligned with a congruent patch of faces on the rhombicosidodecahedron. If two bilunabirotundae are aligned this way on opposite sides of the rhombicosidodecahedron, then a cube can be put between the bilunabirotundae at the very center of the rhombicosidodecahedron.

The rhombicosidodecahedron shares the vertex arrangement with the small stellated truncated dodecahedron, and with the uniform compounds of six or twelve pentagrammic prisms.

The Zometool kits for making geodesic domes and other polyhedra use slotted balls as connectors. The balls are "expanded" rhombicosidodecahedra, with the squares replaced by rectangles. The expansion is chosen so that the resulting rectangles are golden rectangles.

Twelve of the 92 Johnson solids are derived from the rhombicosidodecahedron, four of them by rotation of one or more pentagonal cupolae: the gyrate, parabigyrate, metabigyrate, and trigyrate rhombicosidodecahedron. Eight more can be constructed by removing up to three cupolae, sometimes also rotating one or more of the other cupolae.

Cartesian coordinates

Cartesian coordinates for the vertices of a rhombicosidodecahedron with an edge length of 2 centered at the origin are all even permutations of:
:(±1, ±1, ±''φ''³),
:(±''φ''², ±''φ'', ±2''φ''),
:(±(2+''φ''), 0, ±''φ''²),
where ''φ'' =  is the golden ratio. Therefore, the circumradius of this rhombicosidodecahedron is the common distance of these points from the origin, namely = for edge length 2. For unit edge length, R must be halved, giving
:''R'' = = ≈ 2.233.

Orthogonal projections

The ''rhombicosidodecahedron'' has six special orthogonal projections, centered, on a vertex, on two types of edges, and three types of faces: triangles, squares, and pentagons. The last two correspond to the A₂ and H₂ Coxeter planes.

Spherical tiling

The rhombicosidodecahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Related polyhedra

Symmetry mutations

This polyhedron is topologically related as a part of a sequence of cantellated polyhedra with vertex figure (3.4.n.4), which continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.

Johnson solids

There are 12 related Johnson solids, 5 by diminishment, and 8 including gyrations:

Vertex arrangement

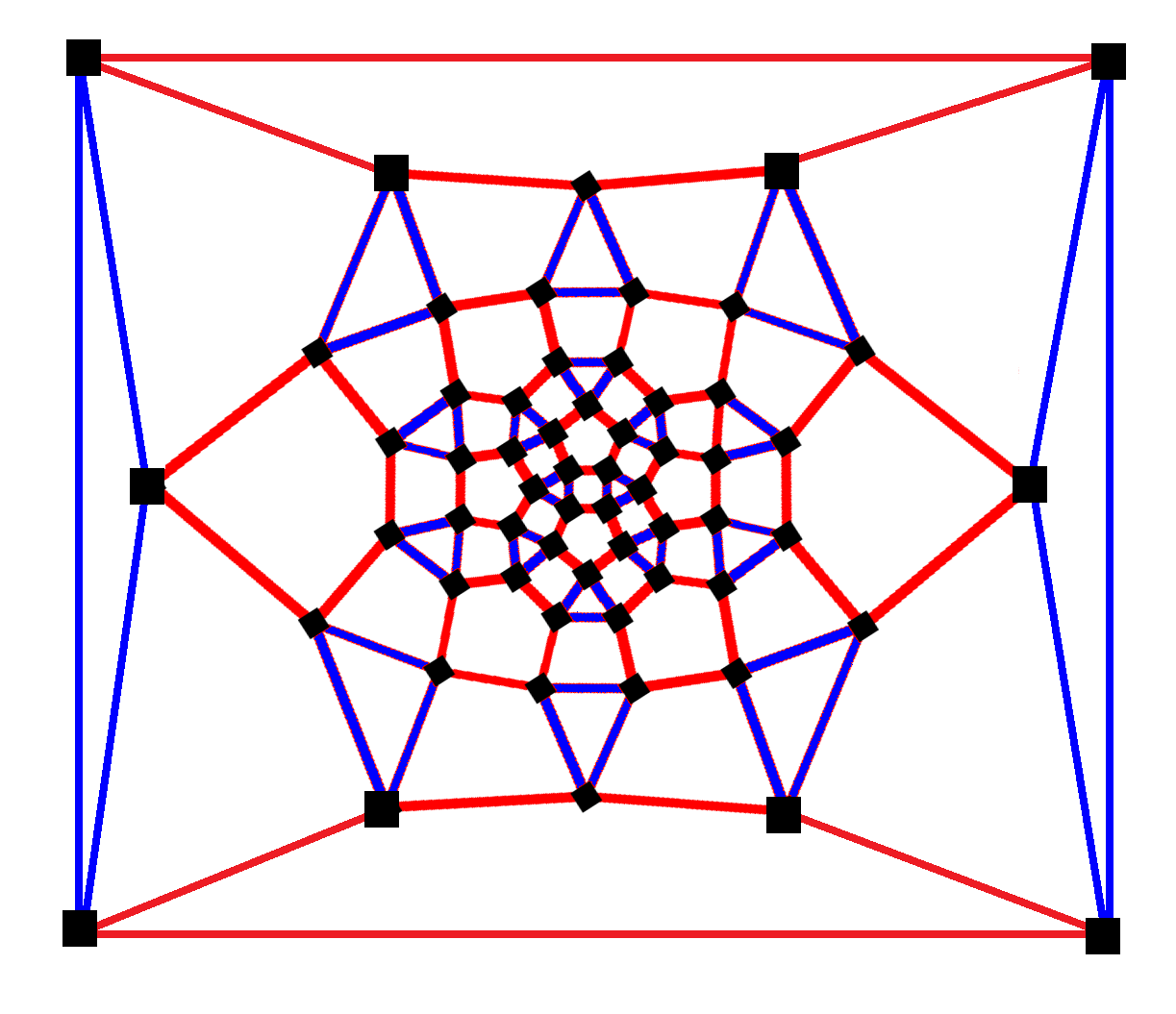
The rhombicosidodecahedron shares its vertex arrangement with three nonconvex uniform polyhedra: the small stellated truncated dodecahedron, the small dodecicosidodecahedron (having the triangular and pentagonal faces in common), and the small rhombidodecahedron (having the square faces in common).

It also shares its vertex arrangement with the uniform compounds of six or twelve pentagrammic prisms.

Rhombicosidodecahedral graph

In the mathematical field of graph theory, a rhombicosidodecahedral graph is the graph of vertices and edges of the rhombicosidodecahedron, one of the Archimedean solids. It has 60 vertices and 120 edges, and is a quartic graph Archimedean graph.

See also

* Truncated rhombicosidodecahedron

Notes

References

* (Section 3-9)
*
*''The Big Bang Theory Series 8 Episode 2 - The Junior Professor Solution'': features this solid as the answer to an impromptu science quiz the main four characters have in Leonard and Sheldon's apartment, and is also illustrated in Chuck Lorre's Vanity Card #461 at the end of that episode.

External links

*
**
*
Editable printable net of a Rhombicosidodecahedron with interactive 3D viewThe Uniform Polyhedra
The Encyclopedia of Polyhedra

{{Polyhedron navigator

Archimedean solids
Uniform polyhedra