|
Cantellation (geometry)
In geometry, a cantellation is a 2nd-order truncation in any dimension that bevels a regular polytope at its edges and at its vertices, creating a new facet in place of each edge and of each vertex. Cantellation also applies to regular tilings and honeycombs. Cantellating a polyhedron is also rectifying its rectification. Cantellation (for polyhedra and tilings) is also called '' expansion'' by Alicia Boole Stott: it corresponds to moving the faces of the regular form away from the center, and filling in a new face in the gap for each opened edge and for each opened vertex. Notation A cantellated polytope is represented by an extended Schläfli symbol ''t''0,2 or ''r''\beginp\\q\\...\end or ''rr''. For polyhedra, a cantellation offers a direct sequence from a regular polyhedron to its dual. Example: cantellation sequence between cube and octahedron: Example: a cuboctahedron is a cantellated tetrahedron. For higher-dimensional polytopes, a cantellation offers a direc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Rhombicuboctahedron
In geometry, the rhombicuboctahedron is an Archimedean solid with 26 faces, consisting of 8 equilateral triangles and 18 squares. It was named by Johannes Kepler in his 1618 Harmonices Mundi, being short for ''truncated cuboctahedral rhombus'', with cuboctahedral rhombus being his name for a rhombic dodecahedron. The rhombicuboctahedron is an Archimedean solid, and its dual is a Catalan solid, the deltoidal icositetrahedron. The elongated square gyrobicupola is a polyhedron that is similar to a rhombicuboctahedron, but it is not an Archimedean solid because it is not vertex-transitive. The rhombicuboctahedron is found in diverse cultures in architecture, toys, the arts, and elsewhere. Construction The rhombicuboctahedron may be constructed from a cube by drawing a smaller one in the middle of each face, parallel to the cube's edges. After removing the edges of a cube, the squares may be joined by adding more squares adjacent between them, and the corners may be filled by th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Polyhedron-33-t0
A uniform is a variety of costume worn by members of an organization while usually participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency services, security guards, in some workplaces and schools, and by inmates in prisons. In some countries, some other officials also wear uniforms in their duties; such is the case of the Commissioned Corps of the United States Public Health Service or the French prefects. For some organizations, such as police, it may be illegal for non-members to wear the uniform. Etymology From the Latin ''unus'' (meaning one), and ''forma'' (meaning form). Variants Corporate and work uniforms Workers sometimes wear uniforms or corporate clothing of one nature or another. Workers required to wear a uniform may include retail workers, bank and post-office workers, public-security and health-care workers, blue-collar employees, personal trainers in he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Tiling
In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of English mathematician John Conway called it a deltille, named from the triangular shape of the Greek letter delta (Δ). The triangular tiling can also be called a kishextille by a kis operation that adds a center point and triangles to replace the faces of a hextille. It is one of three regular tilings of the plane. The other two are the square tiling and the hexagonal tiling. Uniform colorings There are 9 distinct uniform colorings of a triangular tiling. (Naming the colors by indices on the 6 triangles around a vertex: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314) Three of them ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Tiling
In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of or (as a Truncation (geometry), truncated triangular tiling). English mathematician John Horton Conway, John Conway called it a hextille. The internal angle of the hexagon is 120 degrees, so three hexagons at a point make a full 360 degrees. It is one of List of regular polytopes#Euclidean tilings, three regular tilings of the plane. The other two are the triangular tiling and the square tiling. Structure and properties The hexagonal tiling has a structure consisting of a regular hexagon only as its prototile, sharing two vertices with other identical ones, an example of monohedral tiling. Each vertex at the tiling is surrounded by three regular hexagons, denoted as 6.6.6 by vertex configuration. The dual of a hexagonal tiling is triangular tiling, because the center of each hexagonal tiling ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron
In geometry, a dodecahedron (; ) or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Poinsot polyhedron, regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The #Pyritohedron, pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the #Tetartoid, tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling polyhedra, space-filling. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the ( convex, non- stellated) regular icosahedron—one of the Platonic solids—whose faces are 20 equilateral triangles. Regular icosahedra There are two objects, one convex and one nonconvex, that can both be called regular icosahedra. Each has 30 edges and 20 equilateral triangle faces with five meeting at each of its twelve vertices. Both have icosahedral symmetry. The term "regular icosahedron" generally refers to the convex variety, while the nonconvex form is called a ''great icosahedron''. Convex regular icosahedron The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular Platonic solids, and is represented by its Schläfli symbol , contai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex set, convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with 1, unit s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tetrahedron is the simplest of all the ordinary convex polytope, convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean geometry, Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid (geometry), pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such net (polyhedron), nets. For any tetrahedron there exists a sphere (called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
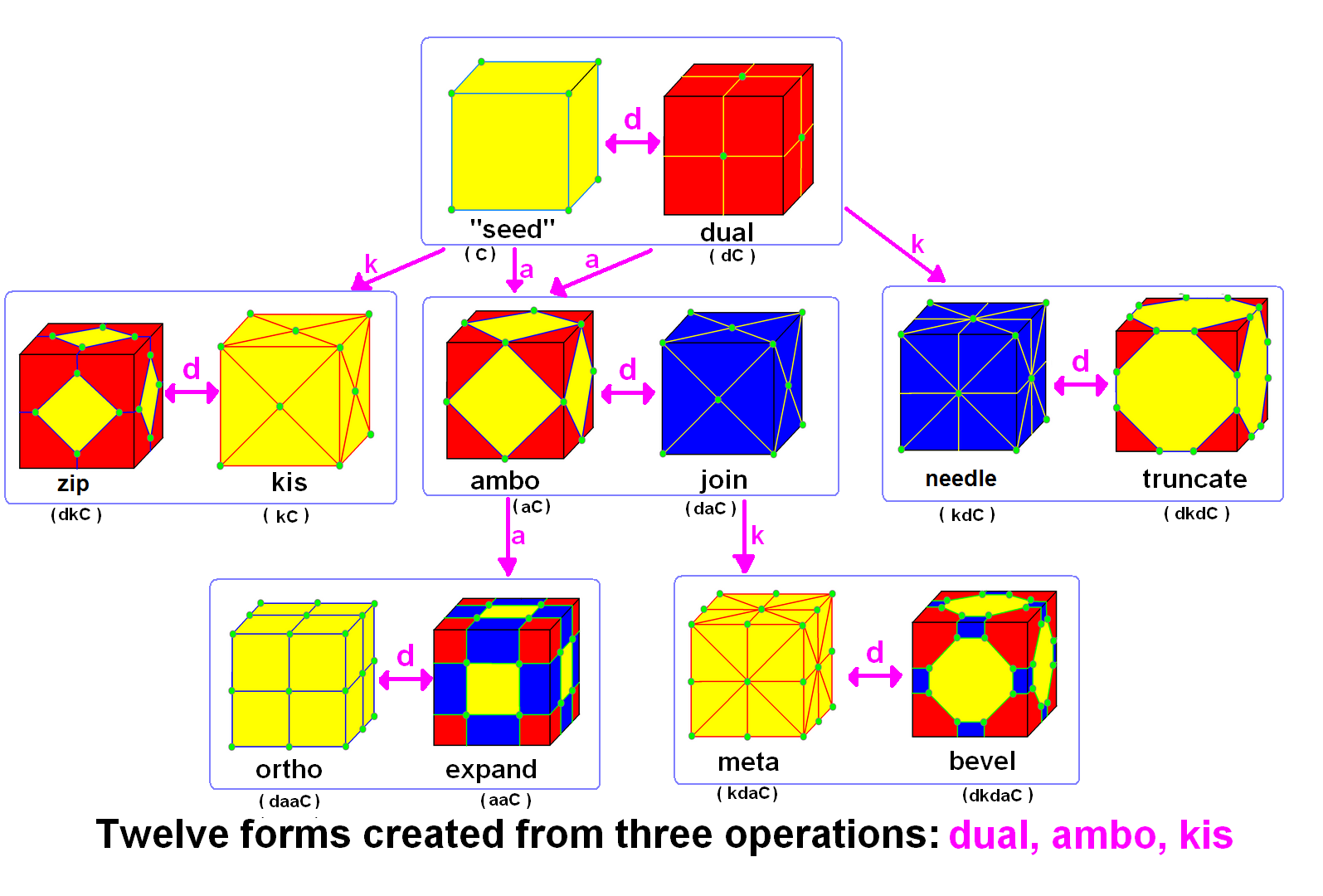
Conway Polyhedron Notation
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is ( topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), ( snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectification (geometry)
In Euclidean geometry, rectification, also known as critical truncation or complete-truncation, is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope. A rectification operator is sometimes denoted by the letter with a Schläfli symbol. For example, is the rectified cube, also called a cuboctahedron, and also represented as \begin 4 \\ 3 \end. And a rectified cuboctahedron is a rhombicuboctahedron, and also represented as r\begin 4 \\ 3 \end. Conway polyhedron notation uses for ambo as this operator. In graph theory this operation creates a medial graph. The rectification of any regular self-dual polyhedron or tiling will result in another regular polyhedron or tiling with a tiling order of 4, for example the tetrahedron becoming an octahedron As a special case, a square til ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |