Lenia

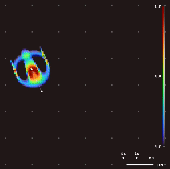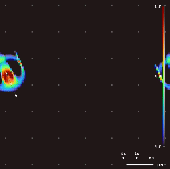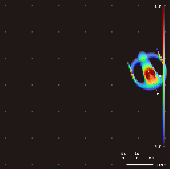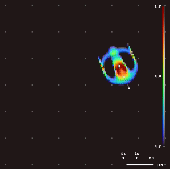
Lenia is a family of cellular automata created by Bert Wang-Chak Chan. It is intended to be a continuous generalization of Conway's Game of Life, with continuous states, space and time. As a consequence of its continuous, high-resolution domain, the complex autonomous patterns ("lifeforms" or " spaceships") generated in Lenia are described as differing from those appearing in other cellular automata, being "geometric, metameric, fuzzy, resilient, adaptive, and rule-generic".

Lenia won the 2018 Virtual Creatures Contest at the Genetic and Evolutionary Computation Conference in Kyoto, an honorable mention for the ALIFE Art Award at ALIFE 2018 in Tokyo, and Outstanding Publication of 2019 by the International Society for Artificial Life (ISAL).

Rules

Iterative updates

Let $\mathcal$ be the ''lattice'' or ''grid'' containing a set of states $S^\mathcal$. Like many cellular automata, Lenia is updated iteratively; each output state is a pure function of the previous state, such that

$\Phi(A^0) = A^, \Phi(A^) = A^, \ldots, \Phi(A^t) = A^,\ldots$

where $A^0$ is the initial state and $\Phi : S^\mathcal \rightarrow S^\mathcal$ is the ''global rule'', representing the application of the ''local rule'' over every site $\mathbf\in\cal$. Thus $\Phi^N(A^t) = A^$.

If the simulation is advanced by $\Delta t$ at each timestep, then the time resolution $T = \frac$.

State sets

Let $S = \$ with maximum $P \in \Z$. This is the ''state set'' of the automaton and characterizes the possible states that may be found at each site. Larger $P$ correspond to higher ''state resolutions'' in the simulation. Many cellular automata use the lowest possible state resolution, i.e. $P = 1$. Lenia allows for much higher resolutions. Note that the actual value at each site is not in ,P/math> but rather an integer multiple of $\Delta p = \frac$; therefore we have $A^t(\mathbf) \in$, 1/math> for all $\mathbf \in \mathcal$. For example, given $P = 4$, $\mathbf^t(\mathbf) \in \$.

Neighborhoods

Mathematically, neighborhoods like those in Game of Life may be represented using a set of position vectors in $\R^2$. For the classic Moore neighborhood used by Game of Life, for instance, $\mathcal = \^2$; i.e. a square of size 3 centered on every site.

In Lenia's case, the neighborhood is instead a ball of radius $R$ centered on a site, $\mathcal = \$, which may include the original site itself.

Note that the neighborhood vectors are not the absolute position of the elements, but rather a set of relative positions (deltas) with respect to any given site.

Local rule

There are discrete and continuous variants of Lenia. Let $\mathbf$ be a vector in $\R^2$ within $\mathcal$ representing the position of a given site, and $\mathcal$ be the set of sites neighboring $\mathbf$. Both variations comprise two stages:

# Using a convolution kernel $\mathbf : \mathcal \rightarrow S$ to compute the ''potential distribution'' $\mathbf^t(\mathbf)=\mathbf * \mathbf^t(\mathbf)$.
# Using a ''growth mapping'' $G :$, 1\rightarrow 1, 1/math> to compute the final ''growth distribution'' $\mathbf^t(\mathbf)=G(\mathbf^t(\mathbf))$.
Once $\mathbf^t$ is computed, it is scaled by the chosen time resolution $\Delta t$ and added to the original state value:$\mathbf^(\mathbf) = \text(\mathbf^ + \Delta t \;\mathbf^t(\mathbf),\; 0,\; 1)$Here, the clip function is defined by $\operatorname(u,a,b):=\min(\max(u,a),b)$ .

The local rules are defined as follows for discrete and continuous Lenia:

$\begin \mathbf^t(\mathbf) &= \begin \sum_ \mathbf\mathbf^t(\mathbf+\mathbf)\Delta x^2, & \text \\ \int_ \mathbf\mathbf^t(\mathbf+\mathbf)dx^2, & \text \end \\ \mathbf^t(\mathbf) &= G(\mathbf^t(\mathbf)) \\ \mathbf^(\mathbf) &= \text(\mathbf^t(\mathbf) + \Delta t\;\mathbf^t(\mathbf),\; 0,\; 1) \end$

Kernel generation

There are many ways to generate the convolution kernel $\mathbf$. The final kernel is the composition of a ''kernel shell'' $K_C$ and a ''kernel skeleton'' $K_S$.

For the kernel shell $K_C$, Chan gives several functions that are defined radially. Kernel shell functions are unimodal and subject to the constraint $K_C(0) = K_C(1) = 0$ (and typically $K_C\left(\frac\right) = 1$ as well). Example kernel functions include:

$K_C(r) = \begin \exp\left(\alpha - \frac\right), & \text, \alpha=4 \\ (4r(1-r))^\alpha, & \text, \alpha=4 \\ \mathbf_(r), & \text \\ \ldots, & \text \end$

Here, $\mathbf_A(r)$ is the indicator function.

Once the kernel shell has been defined, the kernel skeleton $K_S$ is used to expand it and compute the actual values of the kernel by transforming the shell into a series of concentric rings. The height of each ring is controlled by a ''kernel peak'' vector \beta = (\beta_1, \beta_2, \ldots, \beta_B) \in ,1B, where $B$ is the ''rank'' of the parameter vector. Then the kernel skeleton $K_S$ is defined as

$K_S(r;\beta)=\beta_ K_C(Br \text 1)$

The final kernel $\mathbf(\mathbf)$ is therefore

$\mathbf(\mathbf) = \frac$

such that $\mathbf$ is normalized to have an element sum of $1$ and $\mathbf * \mathbf \in$, 1/math> (for conservation of mass). $, K_S, = \textstyle \sum_ \displaystyle K_S \, \Delta x^2$ in the discrete case, and $\int_ K_S \,dx^2$ in the continuous case.

Growth mappings

The growth mapping $G :$, 1\rightarrow 1,1/math>, which is analogous to an activation function, may be any function that is unimodal, nonmonotonic, and accepts parameters $\mu,\sigma \in \R$. Examples include

$G(u;\mu,\sigma) = \begin 2\exp\left(-\frac\right)-1, & \text \\ 2\cdot\mathbf_(u)\left(1-\frac\right)^\alpha-1, & \text, \alpha=4 \\ 2\cdot\mathbf_(u)-1, & \text \\ \ldots, & \text \end$

where $u$ is a potential value drawn from $\mathbf^t$.

Game of Life

The Game of Life may be regarded as a special case of discrete Lenia with $R = T = P = 1$. In this case, the kernel would be rectangular, with the function$K_C(r) = \mathbf_(r) + \frac\mathbf_(r)$and the growth rule also rectangular, with $\mu = 0.35, \sigma = 0.07$.

Patterns

By varying the convolutional kernel, the growth mapping and the initial condition, over 400 "species" of "life" have been discovered in Lenia, displaying "self-organization, self-repair, bilateral and radial symmetries, locomotive dynamics, and sometimes chaotic nature". Chan has created a taxonomy for these patterns.

Related work

Other works have noted the strong similarity between cellular automata update rules and convolutions. Indeed, these works have focused on reproducing cellular automata using simplified convolutional neural networks. Mordvintsev et al. investigated the emergence of self-repairing pattern generation. Gilpin found that any cellular automaton could be represented as a convolutional neural network, and trained neural networks to reproduce existing cellular automata

In this light, cellular automata may be seen as a special case of recurrent convolutional neural networks. Lenia's update rule may also be seen as a single-layer convolution (the "potential field" $\mathbf$) with an activation function (the "growth mapping" $G$). However, Lenia uses far larger, fixed, kernels and is not trained via gradient descent.

See also

* Conway's Game of Life
* Cellular automaton
*Self-replication
*Pattern formation
*Morphogenesis

External links

The Github repository for LeniaAn invited seminar at Stanford given by Chan

References

{{reflist

Cellular automaton rules