|
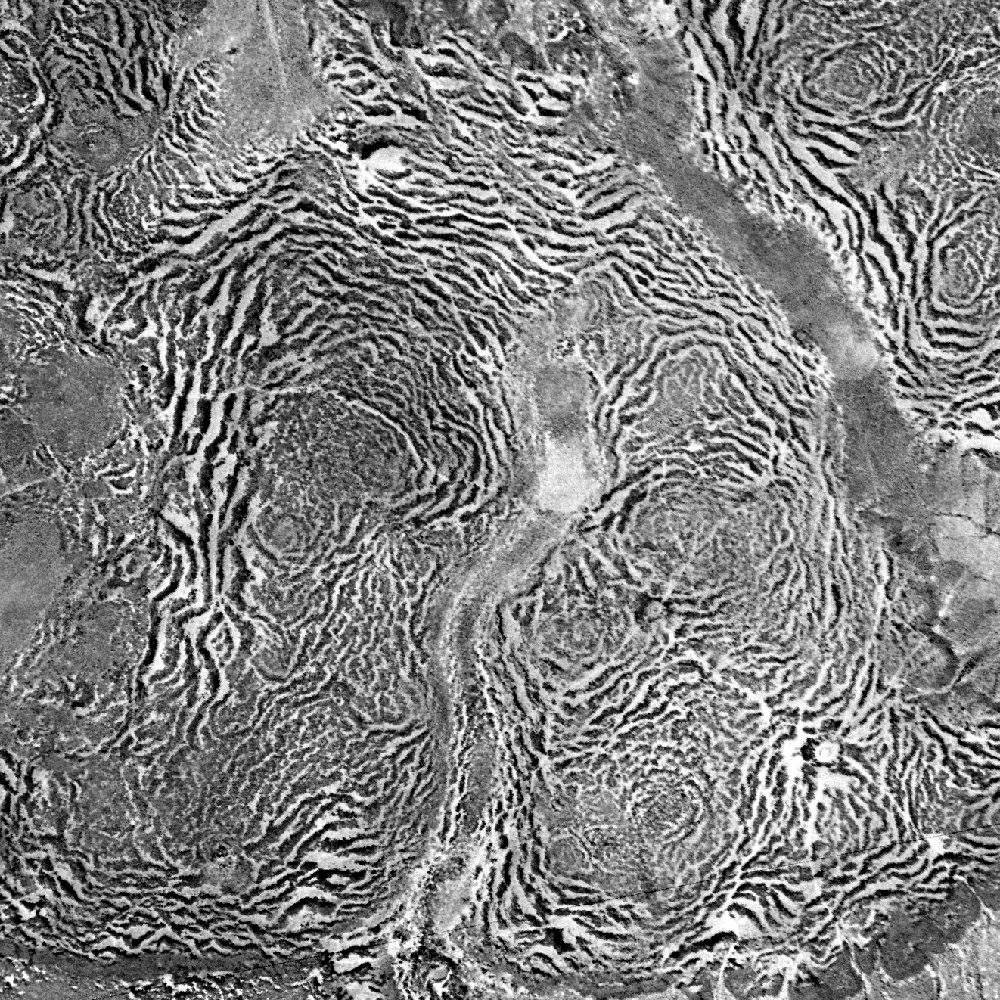
Continuous Spatial Automaton
In automata theory (a subfield of computer science), continuous spatial automata, unlike cellular automata, have a continuum of locations, while the state of a location still is any of a finite number of real numbers. Time can also be continuous, and in this case the state evolves according to differential equations. One important example is reaction–diffusion textures, differential equations proposed by Alan Turing to explain how chemical reactions could create the stripes on zebras and spots on leopards. When these are approximated by CA, such CAs often yield similar patterns. Another important example is neural fields, which are the continuum limit of neural networks where average firing rates evolve based on integro-differential equations. Such models demonstrate spatiotemporal pattern formation, localized states and travelling waves. They have been used as models for cortical memory states and visual hallucinations. MacLennaconsiders continuous spatial automat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automata Theory
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science. The word ''automata'' comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton (automata in plural) is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states (represented in the figure by circles) and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function, which takes the previous state and current input symbol as its arguments. Automata the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Limit
In mathematical physics and mathematics, the continuum limit or scaling limit of a lattice model refers to its behaviour in the limit as the lattice spacing goes to zero. It is often useful to use lattice models to approximate real-world processes, such as Brownian motion. Indeed, according to Donsker's theorem, the discrete random walk would, in the scaling limit, approach the true Brownian motion. Terminology The term ''continuum limit'' mostly finds use in the physical sciences, often in reference to models of aspects of quantum physics, while the term ''scaling limit'' is more common in mathematical use. Application in quantum field theory A lattice model that approximates a continuum quantum field theory in the limit as the lattice spacing goes to zero may correspond to finding a second order phase transition of the model. This is the scaling limit of the model. See also * Universality classes In statistical mechanics, a universality class is a collection of mathematica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analog Computer
An analog computer or analogue computer is a type of computer that uses the continuous variation aspect of physical phenomena such as electrical, mechanical, or hydraulic quantities (''analog signals'') to model the problem being solved. In contrast, digital computers represent varying quantities symbolically and by discrete values of both time and amplitude ( digital signals). Analog computers can have a very wide range of complexity. Slide rules and nomograms are the simplest, while naval gunfire control computers and large hybrid digital/analog computers were among the most complicated. Complex mechanisms for process control and protective relays used analog computation to perform control and protective functions. Analog computers were widely used in scientific and industrial applications even after the advent of digital computers, because at the time they were typically much faster, but they started to become obsolete as early as the 1950s and 1960s, although they ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Travelling Wave
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a ''traveling wave''; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a ''standing wave''. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. Waves are often described by a ''wave equation'' (standing wave field of two opposite waves) or a one-way wave equation for single wave propagation in a defined direction. Two types of waves are most commonly studied in classical physics. In a ''mechanical wave'', stress and strain fields oscillate about a mechanical equilibrium. A mechanical wave is a local deformation (strain) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pattern Formation
The science of pattern formation deals with the visible, (statistically) orderly outcomes of self-organization and the common principles behind similar patterns in nature. In developmental biology, pattern formation refers to the generation of complex organizations of cell fates in space and time. The role of genes in pattern formation is an aspect of morphogenesis, the creation of diverse anatomies from similar genes, now being explored in the science of evolutionary developmental biology or evo-devo. The mechanisms involved are well seen in the anterior-posterior patterning of embryos from the model organism ''Drosophila melanogaster'' (a fruit fly), one of the first organisms to have its morphogenesis studied, and in the eyespots of butterflies, whose development is a variant of the standard (fruit fly) mechanism. Patterns in nature Examples of pattern formation can be found in biology, physics, and science, and can readily be simulated with computer graphics, as desc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatiotemporal Pattern
Spatiotemporal patterns are patterns that occur in a wide range of natural phenoma and are characterized by a spatial and a temporal patterning. The general rules of pattern formation hold. In contrast to "static", pure spatial patterns, the full complexity of spatiotemporal patterns can only be recognized over time. Any kind of traveling wave is a good example of a spatiotemporal pattern. Besides the shape and amplitude of the wave (spatial part), its time-varying position (and possibly shape) in space is an essential part of the entire pattern. The distinction between spatial and spatio-temporal patterns in nature is not clear-cut because a static, invariable pattern will never occur in the strict sense. Even rock formations will slowly change on a time-scale of 10s of millions of years, therefore the distinction lies in the time scale of change in relation to human experience. Already the snapshot state of a dune will usually be taken as an example of a purely spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integro-differential Equation
In mathematics, an integro-differential equation is an equation that involves both integrals and derivatives of a function. General first order linear equations The general first-order, linear (only with respect to the term involving derivative) integro-differential equation is of the form : \fracu(x) + \int_^x f(t,u(t))\,dt = g(x,u(x)), \qquad u(x_0) = u_0, \qquad x_0 \ge 0. As is typical with differential equations, obtaining a closed-form solution can often be difficult. In the relatively few cases where a solution can be found, it is often by some kind of integral transform, where the problem is first transformed into an algebraic setting. In such situations, the solution of the problem may be derived by applying the inverse transform to the solution of this algebraic equation. Example Consider the following second-order problem, : u'(x) + 2u(x) + 5\int_^u(t)\,dt = \theta(x) \qquad \text \qquad u(0)=0, where : \theta(x) = \left\{ \begin{array}{ll} 1, \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neural Networks
A neural network is a network or circuit of biological neurons, or, in a modern sense, an artificial neural network, composed of artificial neurons or nodes. Thus, a neural network is either a biological neural network, made up of biological neurons, or an artificial neural network, used for solving artificial intelligence (AI) problems. The connections of the biological neuron are modeled in artificial neural networks as weights between nodes. A positive weight reflects an excitatory connection, while negative values mean inhibitory connections. All inputs are modified by a weight and summed. This activity is referred to as a linear combination. Finally, an activation function controls the amplitude of the output. For example, an acceptable range of output is usually between 0 and 1, or it could be −1 and 1. These artificial networks may be used for predictive modeling, adaptive control and applications where they can be trained via a dataset. Self-learning resulting from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zebra
Zebras (, ) (subgenus ''Hippotigris'') are African equines with distinctive black-and-white striped coats. There are three living species: the Grévy's zebra (''Equus grevyi''), plains zebra (''E. quagga''), and the mountain zebra (''E. zebra''). Zebras share the genus ''Equus'' with horses and asses, the three groups being the only living members of the family Equidae. Zebra stripes come in different patterns, unique to each individual. Several theories have been proposed for the function of these stripes, with most evidence supporting them as a deterrent for biting flies. Zebras inhabit eastern and southern Africa and can be found in a variety of habitats such as savannahs, grasslands, woodlands, shrublands, and mountainous areas. Zebras are primarily grazers and can subsist on lower-quality vegetation. They are preyed on mainly by lions, and typically flee when threatened but also bite and kick. Zebra species differ in social behaviour, with plains and mounta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (including the design and implementation of hardware and software). Computer science is generally considered an area of academic research and distinct from computer programming. Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and for preventing security vulnerabilities. Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of repositories ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alan Turing
Alan Mathison Turing (; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher, and theoretical biologist. Turing was highly influential in the development of theoretical computer science, providing a formalisation of the concepts of algorithm and computation with the Turing machine, which can be considered a model of a general-purpose computer. He is widely considered to be the father of theoretical computer science and artificial intelligence. Born in Maida Vale, London, Turing was raised in southern England. He graduated at King's College, Cambridge, with a degree in mathematics. Whilst he was a fellow at Cambridge, he published a proof demonstrating that some purely mathematical yes–no questions can never be answered by computation and defined a Turing machine, and went on to prove that the halting problem for Turing machines is undecidable. In 1938, he obtained his PhD from the Department of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |