History Of Classical Mechanics

In physics, mechanics is the study of objects, their interaction, and motion; classical mechanics is mechanics limited to non-relativistic and non-quantum approximations. Most of the techniques of classical mechanics were developed before 1900 so the term classical mechanics refers to that historical era as well as the approximations. Other fields of physics that were developed in the same era, that use the same approximations, and are also considered "classical" include thermodynamics (see history of thermodynamics) and electromagnetism (see history of electromagnetism).

The critical historical event in classical mechanics was the publication by Isaac Newton of his laws of motion and his associated development of the mathematical techniques of calculus in 1678. Analytic tools of mechanics grew through the next two centuries, including the development of Hamiltonian mechanics and the action principles, concepts critical to the development of quantum mechanics and of relativity.

Chaos theory is a subfield of classical mechanics that was developed in its modern form in the 20th century.

Precursors to Newtonian mechanics

Antiquity

The ancient Greek philosophers, Aristotle in particular, were among the first to propose that abstract principles govern nature. Aristotle argued, in ''On the Heavens'', that terrestrial bodies rise or fall to their "natural place" and stated as a law the correct approximation that an object's speed of fall is proportional to its weight and inversely proportional to the density of the fluid it is falling through. Aristotle believed in logic and observation but it would be more than eighteen hundred years before Francis Bacon would first develop the scientific method of experimentation, which he called a ''vexation of nature''.

Aristotle saw a distinction between "natural motion" and "forced motion", and he believed that 'in a void' i.e.vacuum, a body at rest will remain at rest and a body in motion will continue to have the same motion. In this way, Aristotle was the first to approach something similar to the law of inertia. However, he believed a vacuum would be impossible because the surrounding air would rush in to fill it immediately. He also believed that an object would stop moving in an unnatural direction once the applied forces were removed. Later Aristotelians developed an elaborate explanation for why an arrow continues to fly through the air after it has left the bow, proposing that an arrow creates a vacuum in its wake, into which air rushes, pushing it from behind. Aristotle's beliefs were influenced by Plato's teachings on the perfection of the circular uniform motions of the heavens. As a result, he conceived of a natural order in which the motions of the heavens were necessarily perfect, in contrast to the terrestrial world of changing elements, where individuals come to be and pass away.

There is another tradition that goes back to the ancient Greeks where mathematics is used to analyze bodies at rest or in motion, which may found as early as the work of some Pythagoreans. Other examples of this tradition include Euclid (''On the Balance''), Archimedes (''On the Equilibrium of Planes'', ''On Floating Bodies''), and Hero (''Mechanica''). Later, Islamic and Byzantine scholars built on these works, and these ultimately were reintroduced or became available to the West in the 12th century and again during the Renaissance.

Medieval thought

Persian Islamic polymath Ibn Sīnā published his theory of motion in ''The Book of Healing'' (1020). He said that an impetus is imparted to a projectile by the thrower, and viewed it as persistent, requiring external forces such as air resistance to dissipate it. Ibn Sina made distinction between 'force' and 'inclination' (called "mayl"), and argued that an object gained mayl when the object is in opposition to its natural motion. So he concluded that continuation of motion is attributed to the inclination that is transferred to the object, and that object will be in motion until the mayl is spent. He also claimed that projectile in a vacuum would not stop unless it is acted upon. This conception of motion is consistent with Newton's first law of motion, inertia. Which states that an object in motion will stay in motion unless it is acted on by an external force.

In the 12th century, Hibat Allah Abu'l-Barakat al-Baghdaadi adopted and modified Avicenna's theory on projectile motion. In his ''Kitab al-Mu'tabar'', Abu'l-Barakat stated that the mover imparts a violent inclination (''mayl qasri'') on the moved and that this diminishes as the moving object distances itself from the mover. According to Shlomo Pines, al-Baghdaadi's theory of motion was "the oldest negation of Aristotle's fundamental dynamic law amely, that a constant force produces a uniform motion nd is thus ananticipation in a vague fashion of the fundamental law of classical mechanics amely, that a force applied continuously produces acceleration"

In the 14th century, French priest Jean Buridan developed the theory of impetus, with possible influence by Ibn Sina.Sayili, Aydin. "Ibn Sina and Buridan on the Motion the Projectile". Annals of the New York Academy of Sciences vol. 500(1). p.477-482. Albert, Bishop of Halberstadt, developed the theory further.

Nicole Oresme, one of Oxford Calculators at Merton College, Oxford, provided the mean speed theorem using geometrical arguments.

Renaissance

Galileo Galilei's development of the telescope and his observations further challenged the idea that the heavens were made from a perfect, unchanging substance. Adopting Copernicus's heliocentric hypothesis, Galileo believed the Earth was the same as other planets. Though the reality of the famous Tower of Pisa experiment is disputed, he did carry out quantitative experiments by rolling balls on an inclined plane; his correct theory of accelerated motion was apparently derived from the results of the experiments. Galileo also found that a body dropped vertically hits the ground at the same time as a body projected horizontally, so an Earth rotating uniformly will still have objects falling to the ground under gravity. More significantly, it asserted that uniform motion is indistinguishable from rest, and so forms the basis of the theory of relativity. Except with respect to the acceptance of Copernican astronomy, Galileo's direct influence on science in the 17th century outside Italy was probably not very great. Although his influence on educated laymen both in Italy and abroad was considerable, among university professors, except for a few who were his own pupils, it was negligible.

Christiaan Huygens was the foremost mathematician and physicist in Western Europe. He formulated the conservation law for elastic collisions, produced the first theorems of centripetal force, and developed the dynamical theory of oscillating systems. He also made improvements to the telescope, discovered Saturn's moon Titan, and invented the pendulum clock.

Newtonian mechanics

Isaac Newton was the first to unify the three laws of motion (the law of inertia, his second law mentioned above, and the law of action and reaction), and to prove that these laws govern both earthly and celestial objects in 1687 in his treatise ''Philosophiæ Naturalis Principia Mathematica''. Newton and most of his contemporaries hoped that classical mechanics would be able to explain all entities, including (in the form of geometric optics) light.

Newton also developed the calculus which is necessary to perform the mathematical calculations involved in classical mechanics. However it was Gottfried Leibniz who, independently of Newton, developed a calculus with the notation of the derivative and integral which are used to this day. Classical mechanics retains Newton's dot notation for time derivatives.

Leonhard Euler extended Newton's laws of motion from particles to rigid bodies with two additional laws. Working with solid materials under forces leads to deformations that can be quantified. The idea was articulated by Euler (1727), and in 1782 Giordano Riccati began to determine elasticity of some materials, followed by Thomas Young. Simeon Poisson expanded study to the third dimension with the Poisson ratio. Gabriel Lamé drew on the study for assuring stability of structures and introduced the Lamé parameters. These coefficients established linear elasticity theory and started the field of continuum mechanics.

Analytical mechanics

After Newton, re-formulations progressively allowed solutions to a far greater number of problems. The first was constructed in 1788 by Joseph Louis Lagrange- French mathematician. In Lagrangian mechanics the solution uses the path of least action and follows the calculus of variations. William Rowan Hamilton re-formulated Lagrangian mechanics in 1833, resulting in Hamiltonian mechanics. In addition to the solutions of important problems in classical physics, these techniques form the basis for quantum mechanics: Lagrangian methods evolved in to the path integral formulation and the Schrödinger equation builds Hamiltonian mechanics.

In the middle of the 19th century, Hamilton could claim classical mechanics as at the center of attention among scholars:

Origin of chaos theory

In the 1880s, while studying the three-body problem, Henri Poincaré found that there can be orbits that are nonperiodic, and yet not forever increasing nor approaching a fixed point. In 1898, Jacques Hadamard published an influential study of the chaotic motion of a free particle gliding frictionlessly on a surface of constant negative curvature, called Hadamard's billiards. Hadamard was able to show that all trajectories are unstable, in that all particle trajectories diverge exponentially from one another, with a positive Lyapunov exponent.

These developments led in the 20th century to the development of chaos theory.

Conflicts at the end of the 19th century

Although classical mechanics is largely compatible with other "classical physics" theories such as classical electrodynamics and thermodynamics, some difficulties were discovered in the late 19th century that could only be resolved by modern physics. When combined with classical thermodynamics, classical mechanics leads to the Gibbs paradox in which entropy is not a well-defined quantity. As experiments reached the atomic level, classical mechanics failed to explain, even approximately, such basic things as the energy levels and sizes of atoms. The effort at resolving these problems led to the development of quantum mechanics. Action at a distance was still a problem for electromagnetism and Newton's law of universal gravitation, these were temporary explained using aether theories. Similarly, the different behaviour of classical electromagnetism and classical mechanics under velocity transformations led to the Albert Einstein's special relativity.

Modern physics

At the beginning of the 20th century quantum mechanics (1900) and relativistic mechanics (1905) were discovered. This development indicated that classical mechanics was just an approximation of these two theories.

The theory of relativity, introduced by Einstein, would later also include general relativity (1915) that would rewrite gravitational interactions in terms of the curvature of spacetime. Relativistic mechanics recovers Newtonian mechanics and Newton's gravitational law when the speeds involved are much smaller than the speed of light and masses involved are smaller than stellar objects.

Quantum mechanics describing atomic and sub-atomic phenomena was also updated in the 1915 to quantum field theory, that would lead to the Standard Model of elementary particles and elementary interactions like electromagnetism, the strong interaction and the weak interaction. Quantum mechanics recovers classical mechanics at the macroscopic scale in the presence of decoherence.

The unification of general relativity and quantum field theory into a quantum gravity theory is still an open problem in physics.

Later developments

Emmy Noether proved the Noether's theorem in 1918 relating symmetries and conservation laws, it applies to all realms of physics including classical mechanics.

Following the introduction of general relativity, Élie Cartan in 1923 derived Newtonian gravitation from Einstein field equations. This led to Newton–Cartan theory, where classical gravitation can be treated using a geometric formulation of spacetime.

In the 1930s, inspired by quantum mechanics, Bernard Koopman and John von Neumann made some links between Hilbert spaces, wavefunctions and classical mechanics. This discovery led to the development of Koopman–von Neumann classical mechanics.

In 1954, Andrey Kolmogorov revisited the work of Poincaré. He considered the problem of whether or not a small perturbation of a conservative dynamical system resulted in a quasiperiodic orbit in celestial mechanics. The same problem was worked by Jürgen Moser and later by Vladimir Arnold, leading to the Kolmogorov–Arnold–Moser theorem and KAM theory.

Meteorologist Edward Norton Lorenz is often credited as rediscovering the field of chaos theory. About 1961, he discovered that his weather calculations were sensitive to the significant figures in the initial conditions. He later developed the theory of Lorenz system. In 1971, David Ruelle coined the term strange attractor to describe these systems. The term "chaos theory" was finally coined in 1975 by James A. Yorke.

See also

* Mechanics
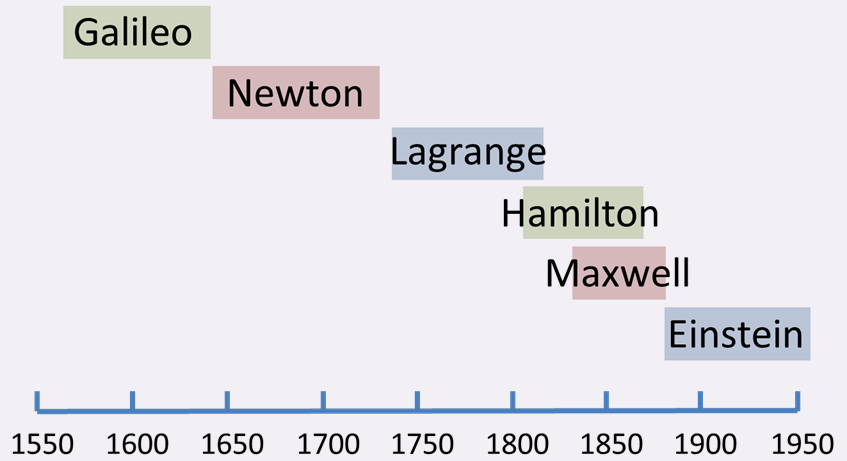
* Timeline of classical mechanics
* History of classical field theory

Notes

References

*
*
*

{{DEFAULTSORT:History Of Classical Mechanics
Classical mechanics
Classical mechanics
Isaac Newton