|
Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution. In physics, Huygens made seminal contributions to optics and mechanics, while as an astronomer he studied the rings of Saturn and discovered its largest moon, Titan (moon), Titan. As an engineer and inventor, he improved the design of telescopes and invented the pendulum clock, the most accurate timekeeper for almost 300 years. A talented mathematician and physicist, his works contain the first idealization of a physical problem by a set of Mathematical model, mathematical parameters, and the first mathematical and mechanistic explanation of an unobservable physical phenomenon.Dijksterhuis, F.J. (2008) Stevin, Huygens and the Dutch republic. ''Nieuw archief voor wiskunde'', ''5'', pp. 100–10/ref> Huygens first identified the correct la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Caspar Netscher
Caspar (or Gaspar) Netscher (1639 – January 15, 1684) was a Dutch portrait and genre painter. He was a master in depicting oriental rugs, silk and brocade and introduced an international style to the Northern Netherlands. Life According to Arnold Houbraken's 17th-century biographical study of Dutch painters he was born in Heidelberg or Prague.Gasper Netscher biography in ''De groote schouburgh der Nederlantsche konstschilders en schilderessen'' (1718) by , courtesy of the Digital library for Dutch literature His father ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Birefringence
Birefringence, also called double refraction, is the optical property of a material having a refractive index that depends on the polarization and propagation direction of light. These optically anisotropic materials are described as birefringent or birefractive. The birefringence is often quantified as the maximum difference between refractive indices exhibited by the material. Crystals with non-cubic crystal structures are often birefringent, as are plastics under mechanical stress. Birefringence is responsible for the phenomenon of double refraction whereby a ray of light, when incident upon a birefringent material, is split by polarization into two rays taking slightly different paths. This effect was first described by Danish scientist Rasmus Bartholin in 1669, who observed it in Iceland spar (calcite) crystals which have one of the strongest birefringences. In the 19th century Augustin-Jean Fresnel described the phenomenon in terms of polarization, understanding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Tritone
A septimal tritone is a tritone (about one half of an octave) that involves the factor seven. There are two that are inverses. The lesser septimal tritone (also Huygens' tritone) is the musical interval with ratio 7:5 (582.51 cents). The greater septimal tritone (also Euler's tritone), is an interval with ratio 10:7 (617.49 cents). They are also known as the sub-fifth and super-fourth, or subminor fifth and supermajor fourth, respectively. The 7:5 interval (diminished fifth) is equal to a 6:5 minor third plus a 7:6 subminor third. The 10:7 interval (augmented fourth) is equal to a 5:4 major third plus an 8:7 supermajor second, or a 9:7 supermajor third plus a 10:9 major second. The difference between these two is the septimal sixth tone (50:49, 34.98 cents) . 12 equal temperament and 22 equal temperament do not distinguish between these tritones; 19 equal temperament does distinguish them but doesn't match them closely. 31 equal temperament and 41 equal temperament both di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
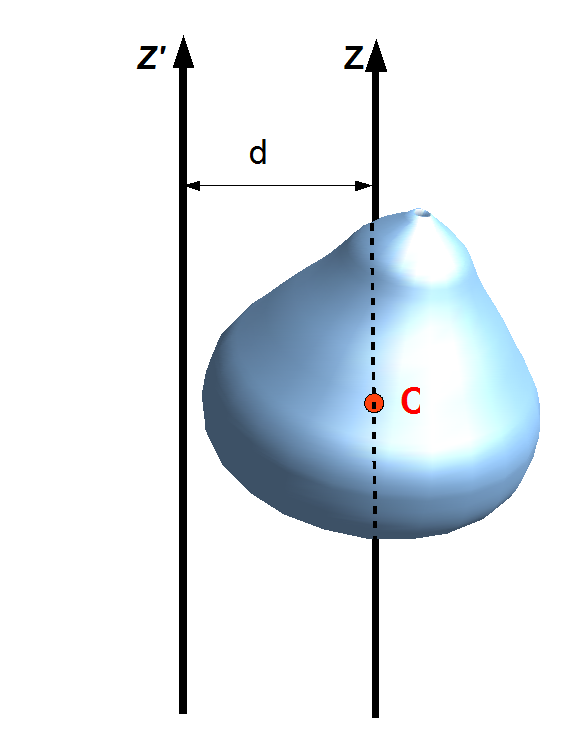
Huygens–Steiner Theorem
The parallel axis theorem, also known as Huygens–Steiner theorem, or just as Steiner's theorem, named after Christiaan Huygens and Jakob Steiner, can be used to determine the moment of inertia or the second moment of area of a rigid body about any axis, given the body's moment of inertia about a Parallel (geometry), parallel axis through the object's center of gravity and the perpendicular distance between the axes. Mass moment of inertia Suppose a body of mass is rotated about an axis passing through the body's center of mass. The body has a moment of inertia with respect to this axis. The parallel axis theorem states that if the body is made to rotate instead about a new axis , which is parallel to the first axis and displaced from it by a distance , then the moment of inertia with respect to the new axis is related to by : I = I_\mathrm + md^2. Explicitly, is the perpendicular distance between the axes and . The parallel axis theorem can be applied with the str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemniscate Of Gerono
In algebraic geometry, the lemniscate of Gerono, or lemniscate of Huygens, or figure-eight curve, is a plane algebraic curve of degree four and genus zero and is a lemniscate curve shaped like an \infty symbol, or figure eight. It has equation :x^4-x^2+y^2 = 0. It was studied by Camille-Christophe Gerono. Parameterization Because the curve is of genus zero, it can be parametrized by rational functions; one means of doing that is :x = \frac,\ y = \frac. Another representation is :x = \cos \varphi,\ y = \sin\varphi\,\cos\varphi = \sin(2\varphi)/2 which reveals that this lemniscate is a special case of a Lissajous figure. Dual curve The dual curve (see Plücker formula In mathematics, a Plücker formula, named after Julius Plücker, is one of a family of formulae, of a type first developed by Plücker in the 1830s, that relate certain numeric invariants of algebraic curves to corresponding invariants of their d ...), pictured below, has therefore a somewhat different chara ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Huygens–Fresnel Principle
The Huygens–Fresnel principle (named after Netherlands, Dutch physicist Christiaan Huygens and France, French physicist Augustin-Jean Fresnel) states that every point on a wavefront is itself the source of spherical wavelets, and the secondary wavelets emanating from different points mutually Wave interference, interfere. The sum of these spherical wavelets forms a new wavefront. As such, the Huygens-Fresnel principle is a method of analysis applied to problems of luminous wave propagation both in the Far-field diffraction pattern, far-field limit and in near-field diffraction as well as Reflection (physics), reflection. History In 1678, Huygens proposed that every point reached by a luminous disturbance becomes a source of a spherical wave. The sum of these secondary waves determines the form of the wave at any subsequent time; the overall procedure is referred to as Huygens' construction. He assumed that the secondary waves travelled only in the "forward" direction, and it is n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Huygenian Eyepiece
An eyepiece, or ocular lens, is a type of lens that is attached to a variety of optical devices such as telescopes and microscopes. It is named because it is usually the lens that is closest to the eye when someone looks through an optical device to observe an object or sample. The objective lens or mirror collects light from an object or sample and brings it to focus creating an image of the object. The eyepiece is placed near the focal point of the objective to magnify this image to the eyes. (The eyepiece and the eye together make an image of the image created by the objective, on the retina of the eye.) The amount of magnification depends on the focal length of the eyepiece. An eyepiece consists of several "lens elements" in a housing, with a "barrel" on one end. The barrel is shaped to fit in a special opening of the instrument to which it is attached. The image can be focused by moving the eyepiece nearer and further from the objective. Most instruments have a focusing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
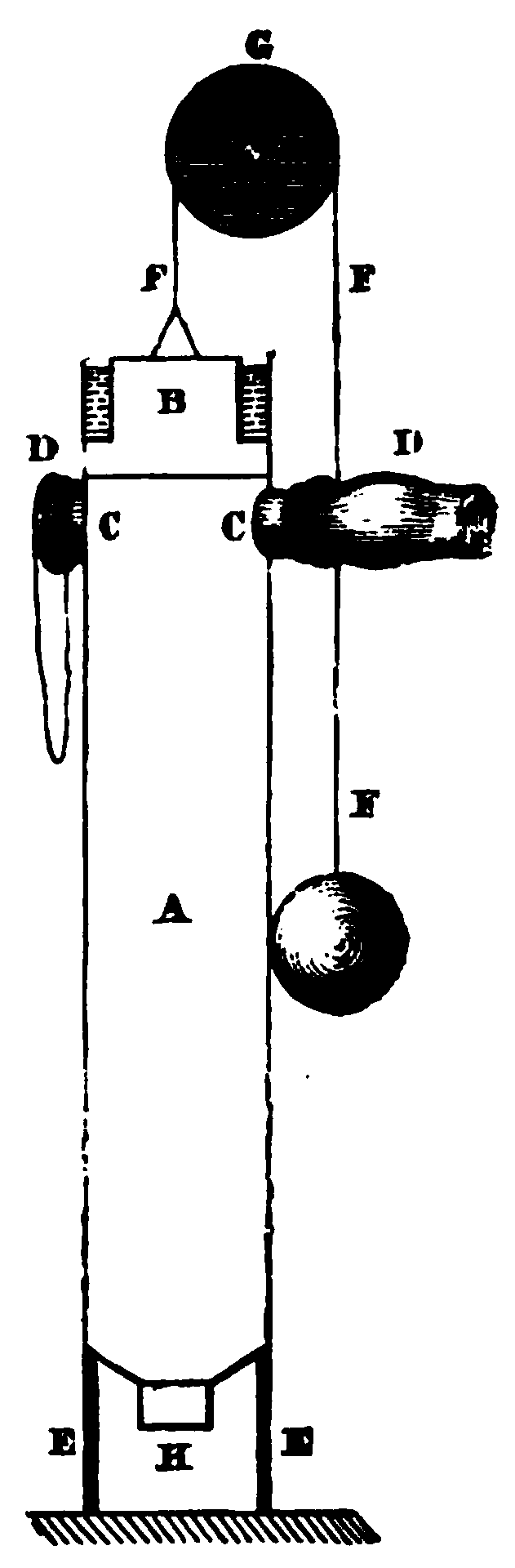
Gunpowder Engine
A gunpowder engine, also known as an explosion engine or Huygens' engine, is a type of internal combustion engine using gunpowder as its fuel. The concept was first explored during the 1600s, most notably by famous Dutch polymath Christiaan Huygens. George Cayley also experimented with the design in the early 1800s as an aircraft engine, and claims to have made models that worked for a short time. There is also a persistent claim that conventional carboretted gasoline engine can be run on gunpowder, but no examples of a successful conversion can be documented. Earliest mentions The gunpowder engine is based on many previous ideas and scientific discoveries, developed by multiple people independently. Early devices just aimed at lifting and/or holding weight (usually to study and demonstrate the physics), while engines aim at doing work continuously (usually with the intention of doing something useful). Vacuum devices to lift/hold weight Leonardo da Vinci described in 1508 a de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gambler's Ruin
In statistics, gambler's ruin is the fact that a gambling, gambler playing a game with negative expected value will eventually go Bankruptcy, bankrupt, regardless of their betting system. The concept was initially stated: A persistent gambler who raises his bet to a fixed fraction of the gambler's bankroll after a win, but does not reduce it after a loss, will eventually and inevitably go broke, even if each bet has a positive expected value. Another statement of the concept is that a persistent gambler with finite wealth, playing a fair game (that is, each bet has expected value of zero to both sides) will eventually and inevitably go broke against an opponent with infinite wealth. Such a situation can be modeled by a random walk on the real number line. In that context, it is probable that the gambler will, with virtual certainty, return to their point of origin, which means going broke, and is ruined an infinite number of times if the random walk continues forever. This is a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolute
In the differential geometry of curves, the evolute of a curve is the locus (mathematics), locus of all its Center of curvature, centers of curvature. That is to say that when the center of curvature of each point on a curve is drawn, the resultant shape will be the evolute of that curve. The evolute of a circle is therefore a single point at its center. Equivalently, an evolute is the envelope (mathematics), envelope of the perpendicular, normals to a curve. The evolute of a curve, a surface, or more generally a submanifold, is the caustic (mathematics), caustic of the normal map. Let be a smooth, regular submanifold in . For each point in and each vector , based at and normal to , we associate the point . This defines a Lagrangian map, called the normal map. The caustic of the normal map is the evolute of . Evolutes are closely connected to involutes: A curve is the evolute of any of its involutes. History Apollonius of Perga, Apollonius ( 200 BC) discussed evolut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saturn's Rings
Saturn has the most extensive and complex ring system of any planet in the Solar System. The rings consist of particles in orbit around the planet made almost entirely of water ice, with a trace component of rocky material. Particles range from micrometers to meters in size. There is no consensus as to what mechanism facilitated their formation: while investigations using theoretical models suggested they formed early in the Solar System's existence, newer data from '' Cassini'' suggests a more recent date of formation. In September 2023, astronomers reported studies suggesting that the rings of Saturn may have resulted from the collision of two moons "a few hundred million years ago". Though light reflected from the rings increases Saturn's apparent brightness, they are not themselves visible from Earth with the naked eye. In 1610, the year after Galileo Galilei's first observations with a telescope, he became the first person to observe Saturn's rings, though he could not se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Titan (moon)
Titan is the largest moon of Saturn and the List of Solar System objects by size, second-largest in the Solar System. It is the only Natural satellite, moon known to have an atmosphere denser than the Atmosphere of Earth, Earth's and is the only known object in space—other than Earth—on which there is clear evidence that stable bodies of liquid exist. Titan is one of seven List of gravitationally rounded objects of the Solar System, gravitationally rounded moons of Saturn and the second-most distant among them. Frequently described as a Planetary-mass moon, planet-like moon, Titan is 50% larger in diameter than Earth's Moon and 80% more Mass, massive. It is the second-largest moon in the Solar System after Jupiter's Ganymede (moon), Ganymede and is larger than Mercury (planet), Mercury; yet Titan is only 40% as massive as Mercury, because Mercury is mainly iron and rock while much of Titan is ice, which is less dense. Discovered in 1655 by the Dutch astronomer Christiaan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |