|
Triangular Cupola
In geometry, the triangular cupola is the cupola with hexagon as its base and triangle as its top. If the edges are equal in length, the triangular cupola is the Johnson solid. It can be seen as half a cuboctahedron. The triangular cupola can be applied to construct many polyhedrons. Properties The triangular cupola has 4 triangles, 3 squares, and 1 hexagon as their faces; the hexagon is the base and one of the four triangles is the top. If all of the edges are equal in length, the triangles and the hexagon becomes regular. The dihedral angle between each triangle and the hexagon is approximately 70.5°, that between each square and the hexagon is 54.7°, and that between square and triangle is 125.3°. A convex polyhedron in which all of the faces are regular is a Johnson solid, and the triangular cupola is among them, enumerated as the third Johnson solid J_ . Given that a is the edge length of a triangular cupola. Its surface area A can be calculated by adding t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Triangular Cupola
In geometry, the elongated triangular cupola is a polyhedron constructed from a hexagonal prism by attaching a triangular cupola. It is an example of a Johnson solid. Construction The elongated triangular cupola is constructed from a hexagonal prism by attaching a triangular cupola onto one of its bases, a process known as the Elongation (geometry), elongation. This cupola covers the hexagonal face so that the resulting polyhedron has four equilateral triangles, nine squares, and one regular hexagon. A convex set, convex polyhedron in which all of the faces are regular polygons is the Johnson solid. The elongated triangular cupola is one of them, enumerated as the eighteenth Johnson solid J_ . Properties The surface area of an elongated triangular cupola A is the sum of all polygonal face's area. The volume of an elongated triangular cupola can be ascertained by dissecting it into a cupola and a hexagonal prism, after which summing their volume. Given the edge length a , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyroelongated Triangular Cupola
In geometry, the gyroelongated triangular cupola is one of the Johnson solids (''J''22). It can be constructed by attaching a hexagonal antiprism to the base of a triangular cupola (''J''3). This is called "gyroelongation", which means that an antiprism is joined to the base of a solid, or between the bases of more than one solid. The gyroelongated triangular cupola can also be seen as a gyroelongated triangular bicupola (''J''44) with one triangular cupola removed. Like all cupolae, the base (geometry), base polygon has twice as many sides as the top (in this case, the bottom polygon is a hexagon because the top is a triangle). Formulae The following formulae for volume and surface area can be used if all face (geometry), faces are regular polygon, regular, with edge length ''a'':Stephen Wolfram,Gyroelongated triangular cupola from Wolfram Alpha. Retrieved July 22, 2010. :V=\left(\frac\sqrt\right)a^3\approx3.51605...a^3 :A=\left(3+\frac\right)a^2\approx12.5263...a^2 Dual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, solids with such a property: the first solids are the Pyramid (geometry), pyramids, Cupola (geometry), cupolas, and a Rotunda (geometry), rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. Definition and background A Johnson solid is a convex polyhedron whose faces are all regular polygons. The convex polyhedron means as bounded intersections of finitely many Half-space (geometry), half-spaces, or as the convex hull of finitely many points. Although there is no restriction that any given regular polygon cannot be a face of a Johnson solid, some authors required that Johnson solids are not Uniform polyhedron, uniform. This means that a Johnson solid is not a Platonic solid, Arc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramidal Symmetry
In three dimensional geometry, there are four infinite series of point groups in three dimensions (''n''≥1) with ''n''-fold rotational or reflectional symmetry about one axis (by an angle of 360°/''n'') that does not change the object. They are the finite symmetry groups on a cone. For ''n'' = ∞ they correspond to four frieze groups. Schönflies notation is used. The terms horizontal (h) and vertical (v) imply the existence and direction of reflections with respect to a vertical axis of symmetry. Also shown are Coxeter notation in brackets, and, in parentheses, orbifold notation. Types ;Chiral: *''Cn'', sup>+, (''nn'') of order ''n'' - ''n''-fold rotational symmetry - acro-n-gonal group (abstract group ''Zn''); for ''n''=1: no symmetry (trivial group) ;Achiral: *''Cnh'', +,2 (''n''*) of order 2''n'' - prismatic symmetry or ortho-n-gonal group (abstract group ''Zn'' × ''Dih1''); for ''n''=1 this is denoted by ''Cs'' (1*) and called reflection symmetry, also bilateral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Truncated Tetrahedron
In geometry, the augmented truncated tetrahedron is a polyhedron constructed by attaching a triangular cupola onto a truncated tetrahedron. It is an example of a Johnson solid. Construction The augmented truncated tetrahedron is constructed from a truncated tetrahedron by attaching a triangular cupola In geometry, the triangular cupola is the cupola with hexagon as its base and triangle as its top. If the edges are equal in length, the triangular cupola is the Johnson solid. It can be seen as half a cuboctahedron. The triangular cupola can b .... This cupola covers one of the truncated tetrahedron's four hexagonal faces, so that the resulting polyhedron's faces are eight equilateral triangles, three squares, and three regular hexagons. Since it has the property of Convex set, convexity and has regular polygonal faces, the augmented truncated tetrahedron is a Johnson solid, denoted as the sixty-fifth Johnson solid J_ . Properties The surface area of an augmented truncat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyroelongated Triangular Bicupola
In geometry, the gyroelongated triangular bicupola is one of the Johnson solids (). As the name suggests, it can be constructed by gyroelongating a triangular bicupola (either triangular orthobicupola, , or the cuboctahedron) by inserting a hexagonal antiprism between its congruent halves. The gyroelongated triangular bicupola is one of five Johnson solids which are chiral, meaning that they have a "left-handed" and a "right-handed" form. In the illustration to the right, each square face on the bottom half of the figure is connected by a path of two triangular faces to a square face above it and to the right. In the figure of opposite chirality (the mirror image of the illustrated figure), each bottom square would be connected to a square face above it and to the left. The two chiral forms of are not considered different Johnson solids. Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Gyr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Triangular Gyrobicupola
In geometry, the elongated triangular gyrobicupola is a polyhedron constructed by attaching two regular triangular cupolas to the base of a regular hexagonal prism, with one of them rotated in 60^\circ . It is an example of Johnson solid. Construction The elongated triangular gyrobicupola is similarly can be constructed as the elongated triangular orthobicupola, started from a hexagonal prism by attaching two regular triangular cupolae onto its base, covering its hexagonal faces. This construction process is known as elongation, giving the resulting polyhedron has 8 equilateral triangles and 12 squares. The difference between those two polyhedrons is one of two triangular cupolas in the elongated triangular gyrobicupola is rotated in 60^\circ . A convex polyhedron in which all faces are regular is Johnson solid, and the elongated triangular gyrobicupola is one among them, enumerated as 36th Johnson solid J_ . Properties An elongated triangular gyrobicupola with a given ed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Triangular Orthobicupola
In geometry, the elongated triangular orthobicupola is a polyhedron constructed by attaching two regular triangular cupola into the base of a regular hexagonal prism. It is an example of Johnson solid. Construction The elongated triangular orthobicupola can be constructed from a hexagonal prism by attaching two regular triangular cupolae onto its base, covering its hexagonal faces. This construction process known as elongation, giving the resulting polyhedron has 8 equilateral triangles and 12 squares. A convex polyhedron in which all faces are regular is Johnson solid, and the elongated triangular orthobicupola is one among them, enumerated as 35th Johnson solid J_ . Properties An elongated triangular orthobicupola with a given edge length a has a surface area, by adding the area of all regular faces: \left(12 + 2\sqrt\right)a^2 \approx 15.464a^2. Its volume can be calculated by cutting it off into two triangular cupolae and a hexagonal prism with regular faces, and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Orthobicupola
In geometry, the triangular orthobicupola is one of the Johnson solids (). As the name suggests, it can be constructed by attaching two triangular cupolas () along their bases. It has an equal number of squares and triangles at each vertex; however, it is not vertex-transitive. It is also called an ''anticuboctahedron'', ''twisted cuboctahedron'' or ''disheptahedron''. It is also a canonical polyhedron. The ''triangular orthobicupola'' is the first in an infinite set of orthobicupolae. Construction The ''triangular orthobicupola'' can be constructed by attaching two triangular cupolas onto their bases. Similar to the cuboctahedron, which would be known as the ''triangular gyrobicupola'', the difference is that the two triangular cupolas that make up the triangular orthobicupola are joined so that pairs of matching sides abut (hence, "ortho"); the cuboctahedron is joined so that triangles abut squares and vice versa. Given a triangular orthobicupola, a 60-degree rotation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyroelongation
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two solids with such a property: the first solids are the pyramids, cupolas, and a rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. Definition and background A Johnson solid is a convex polyhedron whose faces are all regular polygons. The convex polyhedron means as bounded intersections of finitely many half-spaces, or as the convex hull of finitely many points. Although there is no restriction that any given regular polygon cannot be a face of a Johnson solid, some authors required that Johnson solids are not uniform. This means that a Johnson solid is not a Platonic solid, Archimedean solid, prism, or antiprism. A convex polyhedron in which all faces are nearly regular, but some are not pre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
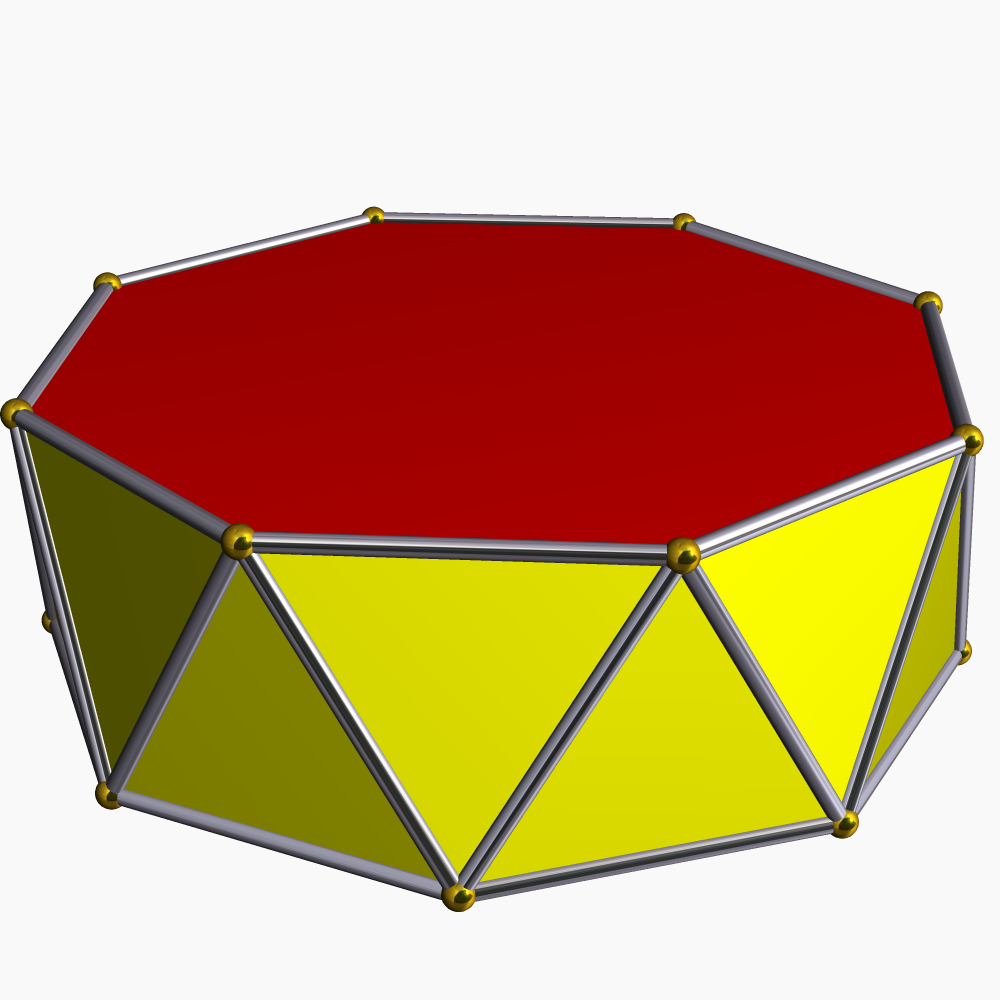
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |