|
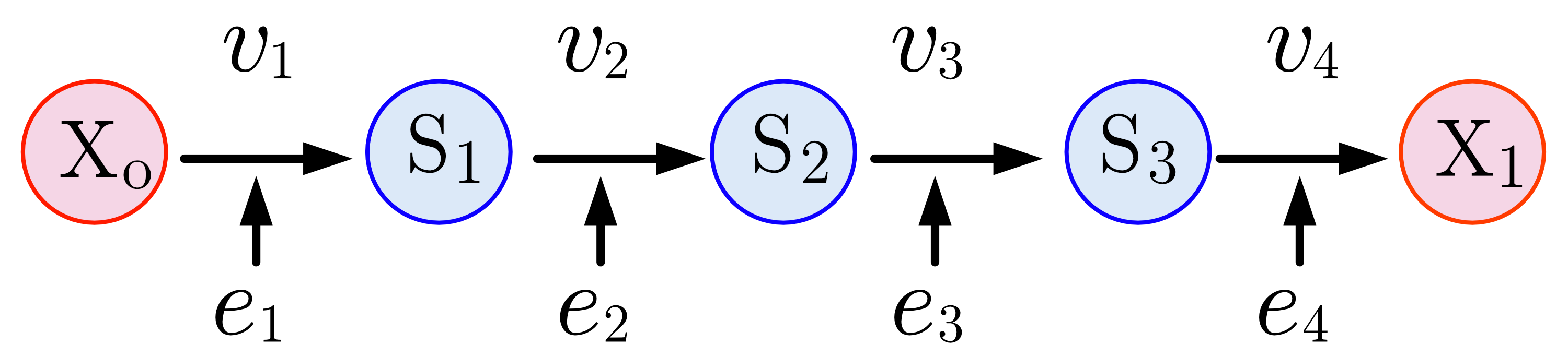
Linear Biochemical Pathway
A linear biochemical pathway is a chain of Enzyme catalysis, enzyme-catalyzed reaction steps where the product of one reaction becomes the Substrate (chemistry), substrate for the next Chemical reaction, reaction. The molecules progress through the pathway sequentially from the starting substrate to the final product. Each step in the pathway is usually facilitated by a different specific enzyme that Catalysis, catalyzes the chemical transformation. An example includes DNA replication, which connects the starting substrate and the end product in a straightforward sequence. Biological cells consume Nutrient, nutrients to sustain life. These nutrients are broken down to smaller molecules. Some of the molecules are used in the cells for various biological functions, and others are reassembled into more complex structures required for life. The breakdown and reassembly of nutrients is called metabolism. An individual cell contains thousands of different kinds of small molecules, su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enzyme Catalysis
Enzyme catalysis is the increase in the rate of a process by an "enzyme", a biological molecule. Most enzymes are proteins, and most such processes are chemical reactions. Within the enzyme, generally catalysis occurs at a localized site, called the active site. Most enzymes are made predominantly of proteins, either a single protein chain or many such chains in a multi-subunit complex. Enzymes often also incorporate non-protein components, such as metal ions or specialized organic molecules known as cofactor (e.g. adenosine triphosphate). Many cofactors are vitamins, and their role as vitamins is directly linked to their use in the catalysis of biological process within metabolism. Catalysis of biochemical reactions in the cell is vital since many but not all metabolically essential reactions have very low rates when uncatalysed. One driver of protein evolution is the optimization of such catalytic activities, although only the most crucial enzymes operate near catalytic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four Step Pathway
4 (four) is a number, numeral and digit. It is the natural number following 3 and preceding 5. It is a square number, the smallest semiprime and composite number, and is considered unlucky in many East Asian cultures. Evolution of the Hindu-Arabic digit Brahmic numerals represented 1, 2, and 3 with as many lines. 4 was simplified by joining its four lines into a cross that looks like the modern plus sign. The Shunga would add a horizontal line on top of the digit, and the Kshatrapa and Pallava evolved the digit to a point where the speed of writing was a secondary concern. The Arabs' 4 still had the early concept of the cross, but for the sake of efficiency, was made in one stroke by connecting the "western" end to the "northern" end; the "eastern" end was finished off with a curve. The Europeans dropped the finishing curve and gradually made the digit less cursive, ending up with a digit very close to the original Brahmin cross. While the shape of the character fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flux (metabolism)
In biochemistry, metabolic flux (often referred to as flux) is the rate of turnover of molecules through a metabolic pathway. Flux is regulated by the enzymes involved in a pathway. Within cells, regulation of flux is vital for all metabolic pathways to regulate the pathway's activity under different conditions. Flux is therefore of great interest in metabolic network modelling, where it is analysed via flux balance analysis and metabolic control analysis. In this manner, flux is the movement of matter through metabolic networks that are connected by metabolites and cofactors, and is therefore a way of describing the activity of the metabolic network as a whole using a single characteristic. Metabolic flux It is easiest to describe the flux of metabolites through a pathway by considering the reaction steps individually. The flux of the metabolites through each reaction () is the rate of the forward reaction (), less that of the reverse reaction (): J = V_f - V_r At eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilibrium Constant
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the Chemical equilibrium#Composition of a mixture, composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant. A knowledge of equilibrium constants is essential for the understanding of many chemical systems, as well as the biochemical processes such as oxygen transport by hemoglobin in blood and acid–base homeostasis in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Mass Action
In chemistry, the law of mass action is the proposition that the rate of a chemical reaction is directly proportional to the product of the activities or concentrations of the reactants. It explains and predicts behaviors of solutions in dynamic equilibrium. Specifically, it implies that for a chemical reaction mixture that is in equilibrium, the ratio between the concentration of reactants and products is constant. Two aspects are involved in the initial formulation of the law: 1) the equilibrium aspect, concerning the composition of a reaction mixture at equilibrium and 2) the kinetic aspect concerning the rate equations for elementary reactions. Both aspects stem from the research performed by Cato M. Guldberg and Peter Waage between 1864 and 1879 in which equilibrium constants were derived by using kinetic data and the rate equation which they had proposed. Guldberg and Waage also recognized that chemical equilibrium is a dynamic process in which rates of reaction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Of Mass
In physics and chemistry, the law of conservation of mass or principle of mass conservation states that for any system closed to all transfers of matter the mass of the system must remain constant over time. The law implies that mass can neither be created nor destroyed, although it may be rearranged in space, or the entities associated with it may be changed in form. For example, in chemical reactions, the mass of the chemical components before the reaction is equal to the mass of the components after the reaction. Thus, during any chemical reaction and low-energy thermodynamic processes in an isolated system, the total mass of the reactants, or starting materials, must be equal to the mass of the products. The concept of mass conservation is widely used in many fields such as chemistry, mechanics, and fluid dynamics. Historically, mass conservation in chemical reactions was primarily demonstrated in the 17th century and finally confirmed by Antoine Lavoisier in the late 18 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear System
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems. Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearization
In mathematics, linearization (British English: linearisation) is finding the linear approximation to a function at a given point. The linear approximation of a function is the first order Taylor expansion around the point of interest. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or discrete dynamical systems. This method is used in fields such as engineering, physics, economics, and ecology. Linearization of a function Linearizations of a function are lines—usually lines that can be used for purposes of calculation. Linearization is an effective method for approximating the output of a function y = f(x) at any x = a based on the value and slope of the function at x = b, given that f(x) is differentiable on , b/math> (or , a/math>) and that a is close to b. In short, linearization approximates the output of a function near x = a. For example, \sq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
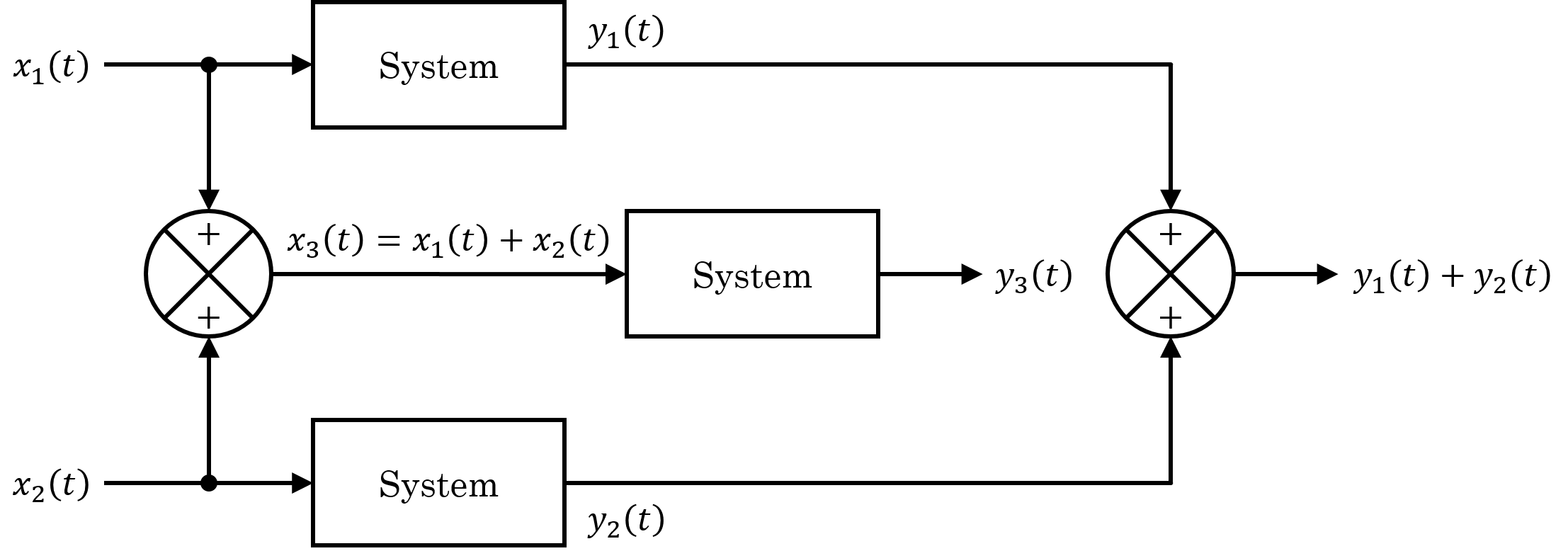
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |