Linear system on:
[Wikipedia]
[Google]
[Amazon]
In systems theory, a linear system is a mathematical model of a
 A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description.
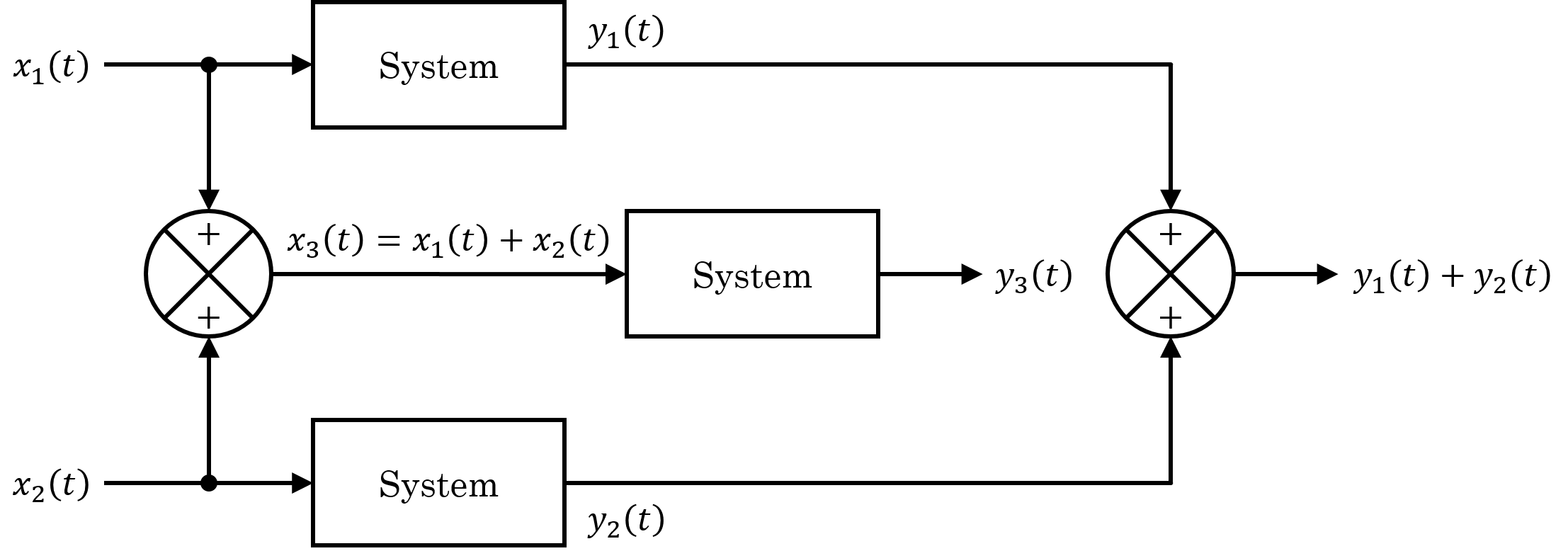
A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.)
The superposition principle means that a linear combination of inputs to the system produces a linear combination of the individual zero-state outputs (that is, outputs setting the initial conditions to zero) corresponding to the individual inputs.
In a system that satisfies the homogeneity property, scaling the input always results in scaling the zero-state response by the same factor. In a system that satisfies the additivity property, adding two inputs always results in adding the corresponding two zero-state responses due to the individual inputs.
Mathematically, for a continuous-time system, given two arbitrary inputs
as well as their respective zero-state outputs
then a linear system must satisfy
for any scalar values and , for any input signals and , and for all time .
The system is then defined by the equation , where is some arbitrary function of time, and is the system state. Given and the system can be solved for
The behavior of the resulting system subjected to a complex input can be described as a sum of responses to simpler inputs. In nonlinear systems, there is no such relation.
This mathematical property makes the solution of modelling equations simpler than many nonlinear systems.
For time-invariant systems this is the basis of the impulse response or the frequency response methods (see LTI system theory), which describe a general input function in terms of unit impulses or frequency components.
Typical differential equations of linear time-invariant systems are well adapted to analysis using the Laplace transform in the continuous case, and the Z-transform in the discrete case (especially in computer implementations).
Another perspective is that solutions to linear systems comprise a system of functions which act like vectors in the geometric sense.
A common use of linear models is to describe a nonlinear system by linearization. This is usually done for mathematical convenience.
The previous definition of a linear system is applicable to SISO (single-input single-output) systems. For MIMO (multiple-input multiple-output) systems, input and output signal vectors (, , , ) are considered instead of input and output signals (, , , .)
This definition of a linear system is analogous to the definition of a linear differential equation in
A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description.
A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.)
The superposition principle means that a linear combination of inputs to the system produces a linear combination of the individual zero-state outputs (that is, outputs setting the initial conditions to zero) corresponding to the individual inputs.
In a system that satisfies the homogeneity property, scaling the input always results in scaling the zero-state response by the same factor. In a system that satisfies the additivity property, adding two inputs always results in adding the corresponding two zero-state responses due to the individual inputs.
Mathematically, for a continuous-time system, given two arbitrary inputs
as well as their respective zero-state outputs
then a linear system must satisfy
for any scalar values and , for any input signals and , and for all time .
The system is then defined by the equation , where is some arbitrary function of time, and is the system state. Given and the system can be solved for
The behavior of the resulting system subjected to a complex input can be described as a sum of responses to simpler inputs. In nonlinear systems, there is no such relation.
This mathematical property makes the solution of modelling equations simpler than many nonlinear systems.
For time-invariant systems this is the basis of the impulse response or the frequency response methods (see LTI system theory), which describe a general input function in terms of unit impulses or frequency components.
Typical differential equations of linear time-invariant systems are well adapted to analysis using the Laplace transform in the continuous case, and the Z-transform in the discrete case (especially in computer implementations).
Another perspective is that solutions to linear systems comprise a system of functions which act like vectors in the geometric sense.
A common use of linear models is to describe a nonlinear system by linearization. This is usually done for mathematical convenience.
The previous definition of a linear system is applicable to SISO (single-input single-output) systems. For MIMO (multiple-input multiple-output) systems, input and output signal vectors (, , , ) are considered instead of input and output signals (, , , .)
This definition of a linear system is analogous to the definition of a linear differential equation in
system
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
based on the use of a linear operator.
Linear systems typically exhibit features and properties that are much simpler than the nonlinear case.
As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomograph ...
, and telecommunications
Telecommunication, often used in its plural form or abbreviated as telecom, is the transmission of information over a distance using electronic means, typically through cables, radio waves, or other communication technologies. These means of ...
. For example, the propagation medium for wireless communication systems can often be
modeled by linear systems.
Definition

 A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description.
A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.)
The superposition principle means that a linear combination of inputs to the system produces a linear combination of the individual zero-state outputs (that is, outputs setting the initial conditions to zero) corresponding to the individual inputs.
In a system that satisfies the homogeneity property, scaling the input always results in scaling the zero-state response by the same factor. In a system that satisfies the additivity property, adding two inputs always results in adding the corresponding two zero-state responses due to the individual inputs.
Mathematically, for a continuous-time system, given two arbitrary inputs
as well as their respective zero-state outputs
then a linear system must satisfy
for any scalar values and , for any input signals and , and for all time .
The system is then defined by the equation , where is some arbitrary function of time, and is the system state. Given and the system can be solved for
The behavior of the resulting system subjected to a complex input can be described as a sum of responses to simpler inputs. In nonlinear systems, there is no such relation.
This mathematical property makes the solution of modelling equations simpler than many nonlinear systems.
For time-invariant systems this is the basis of the impulse response or the frequency response methods (see LTI system theory), which describe a general input function in terms of unit impulses or frequency components.
Typical differential equations of linear time-invariant systems are well adapted to analysis using the Laplace transform in the continuous case, and the Z-transform in the discrete case (especially in computer implementations).
Another perspective is that solutions to linear systems comprise a system of functions which act like vectors in the geometric sense.
A common use of linear models is to describe a nonlinear system by linearization. This is usually done for mathematical convenience.
The previous definition of a linear system is applicable to SISO (single-input single-output) systems. For MIMO (multiple-input multiple-output) systems, input and output signal vectors (, , , ) are considered instead of input and output signals (, , , .)
This definition of a linear system is analogous to the definition of a linear differential equation in
A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description.
A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.)
The superposition principle means that a linear combination of inputs to the system produces a linear combination of the individual zero-state outputs (that is, outputs setting the initial conditions to zero) corresponding to the individual inputs.
In a system that satisfies the homogeneity property, scaling the input always results in scaling the zero-state response by the same factor. In a system that satisfies the additivity property, adding two inputs always results in adding the corresponding two zero-state responses due to the individual inputs.
Mathematically, for a continuous-time system, given two arbitrary inputs
as well as their respective zero-state outputs
then a linear system must satisfy
for any scalar values and , for any input signals and , and for all time .
The system is then defined by the equation , where is some arbitrary function of time, and is the system state. Given and the system can be solved for
The behavior of the resulting system subjected to a complex input can be described as a sum of responses to simpler inputs. In nonlinear systems, there is no such relation.
This mathematical property makes the solution of modelling equations simpler than many nonlinear systems.
For time-invariant systems this is the basis of the impulse response or the frequency response methods (see LTI system theory), which describe a general input function in terms of unit impulses or frequency components.
Typical differential equations of linear time-invariant systems are well adapted to analysis using the Laplace transform in the continuous case, and the Z-transform in the discrete case (especially in computer implementations).
Another perspective is that solutions to linear systems comprise a system of functions which act like vectors in the geometric sense.
A common use of linear models is to describe a nonlinear system by linearization. This is usually done for mathematical convenience.
The previous definition of a linear system is applicable to SISO (single-input single-output) systems. For MIMO (multiple-input multiple-output) systems, input and output signal vectors (, , , ) are considered instead of input and output signals (, , , .)
This definition of a linear system is analogous to the definition of a linear differential equation in calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
, and a linear transformation in linear algebra.
Examples
Asimple harmonic oscillator
In mechanics and physics, simple harmonic motion (sometimes abbreviated as ) is a special type of periodic function, periodic motion an object experiences by means of a restoring force whose magnitude is directly proportionality (mathematics), ...
obeys the differential equation:
If
then is a linear operator. Letting we can rewrite the differential equation as which shows that a simple harmonic oscillator is a linear system.
Other examples of linear systems include those described by , , , and any system described by ordinary linear differential equations. Systems described by , , , , , , , and a system with odd-symmetry output consisting of a linear region and a saturation (constant) region, are non-linear because they don't always satisfy the superposition principle.
The output versus input graph of a linear system need not be a straight line through the origin. For example, consider a system described by (such as a constant-capacitance capacitor or a constant-inductance inductor). It is linear because it satisfies the superposition principle. However, when the input is a sinusoid, the output is also a sinusoid, and so its output-input plot is an ellipse centered at the origin rather than a straight line passing through the origin.
Also, the output of a linear system can contain harmonics (and have a smaller fundamental frequency than the input) even when the input is a sinusoid. For example, consider a system described by . It is linear because it satisfies the superposition principle. However, when the input is a sinusoid of the form , using product-to-sum trigonometric identities it can be easily shown that the output is , that is, the output doesn't consist only of sinusoids of same frequency as the input (), but instead also of sinusoids of frequencies and ; furthermore, taking the least common multiple of the fundamental period of the sinusoids of the output, it can be shown the fundamental angular frequency of the output is , which is different than that of the input.
Time-varying impulse response
The time-varying impulse response of a linear system is defined as the response of the system at time ''t'' = ''t''2 to a single impulse applied at time In other words, if the input to a linear system is where represents the Dirac delta function, and the corresponding response of the system is then the function is the time-varying impulse response of the system. Since the system cannot respond before the input is applied the following causality condition must be satisfied:The convolution integral
The output of any general continuous-time linear system is related to the input by an integral which may be written over a doubly infinite range because of the causality condition: If the properties of the system do not depend on the time at which it is operated then it is said to be time-invariant and is a function only of the time difference which is zero for (namely ). By redefinition of it is then possible to write the input-output relation equivalently in any of the ways, Linear time-invariant systems are most commonly characterized by the Laplace transform of the impulse response function called the ''transfer function'' which is: In applications this is usually a rational algebraic function of . Because is zero for negative , the integral may equally be written over the doubly infinite range and putting follows the formula for the ''frequency response function'':Discrete-time systems
The output of any discrete time linear system is related to the input by the time-varying convolution sum: or equivalently for a time-invariant system on redefining , where represents the lag time between the stimulus at time ''m'' and the response at time ''n''.See also
* Shift invariant system * Linear control * Linear time-invariant system * Nonlinear system * System analysis * System of linear equationsReferences
{{DEFAULTSORT:Linear System Systems theory Dynamical systems Mathematical modeling Concepts in physics