Linear Biochemical Pathway on:
[Wikipedia]
[Google]
[Amazon]
A linear biochemical pathway is a chain of enzyme-catalyzed reaction steps where the product of one reaction becomes the 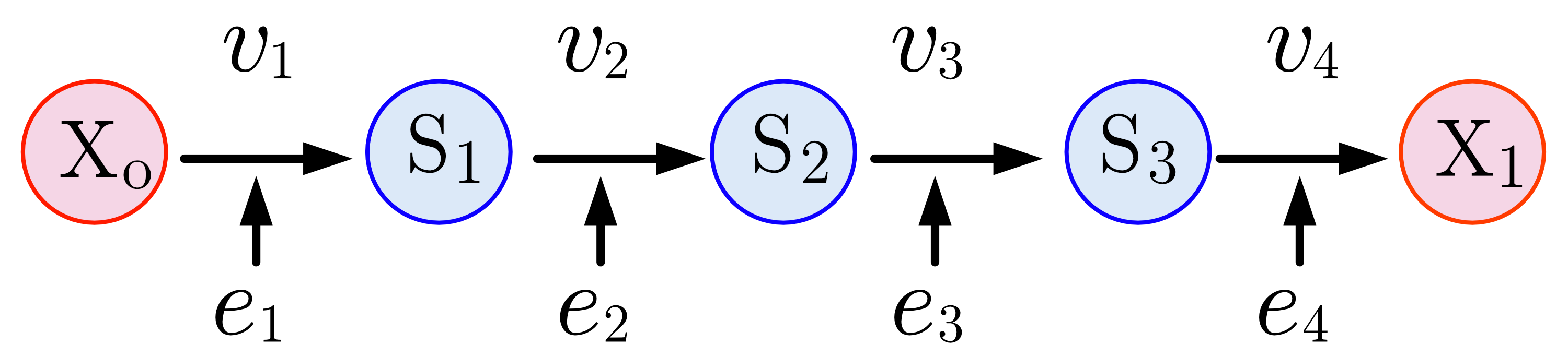 A linear pathway can be studied in various ways. Multiple
A linear pathway can be studied in various ways. Multiple
substrate
Substrate may refer to:
Physical layers
*Substrate (biology), the natural environment in which an organism lives, or the surface or medium on which an organism grows or is attached
** Substrate (aquatic environment), the earthy material that exi ...
for the next reaction
Reaction may refer to a process or to a response to an action, event, or exposure.
Physics and chemistry
*Chemical reaction
*Nuclear reaction
*Reaction (physics), as defined by Newton's third law
* Chain reaction (disambiguation)
Biology and ...
. The molecules progress through the pathway sequentially from the starting substrate to the final product. Each step in the pathway is usually facilitated by a different specific enzyme
An enzyme () is a protein that acts as a biological catalyst by accelerating chemical reactions. The molecules upon which enzymes may act are called substrate (chemistry), substrates, and the enzyme converts the substrates into different mol ...
that catalyzes
Catalysis () is the increase in rate of a chemical reaction due to an added substance known as a catalyst (). Catalysts are not consumed by the reaction and remain unchanged after it. If the reaction is rapid and the catalyst recycles quick ...
the chemical transformation. An example includes DNA replication
In molecular biology, DNA replication is the biological process of producing two identical replicas of DNA from one original DNA molecule. DNA replication occurs in all life, living organisms, acting as the most essential part of heredity, biolog ...
, which connects the starting substrate and the end product in a straightforward sequence.
Biological cells consume nutrients
A nutrient is a substance used by an organism to survive, grow and reproduce. The requirement for dietary nutrient intake applies to animals, plants, fungi and protists. Nutrients can be incorporated into cells for metabolic purposes or excret ...
to sustain life. These nutrients are broken down to smaller molecule
A molecule is a group of two or more atoms that are held together by Force, attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemi ...
s. Some of the molecules are used in the cells for various biological functions, and others are reassembled into more complex structures required for life. The breakdown and reassembly of nutrients is called metabolism
Metabolism (, from ''metabolē'', "change") is the set of life-sustaining chemical reactions in organisms. The three main functions of metabolism are: the conversion of the energy in food to energy available to run cellular processes; the co ...
. An individual cell contains thousands of different kinds of small molecules, such as sugar
Sugar is the generic name for sweet-tasting, soluble carbohydrates, many of which are used in food. Simple sugars, also called monosaccharides, include glucose
Glucose is a sugar with the Chemical formula#Molecular formula, molecul ...
s, lipid
Lipids are a broad group of organic compounds which include fats, waxes, sterols, fat-soluble vitamins (such as vitamins A, D, E and K), monoglycerides, diglycerides, phospholipids, and others. The functions of lipids include storing ...
s, and amino acid
Amino acids are organic compounds that contain both amino and carboxylic acid functional groups. Although over 500 amino acids exist in nature, by far the most important are the 22 α-amino acids incorporated into proteins. Only these 22 a ...
s. The interconversion of these molecules is carried out by catalyst
Catalysis () is the increase in rate of a chemical reaction due to an added substance known as a catalyst (). Catalysts are not consumed by the reaction and remain unchanged after it. If the reaction is rapid and the catalyst recycles quick ...
s called enzyme
An enzyme () is a protein that acts as a biological catalyst by accelerating chemical reactions. The molecules upon which enzymes may act are called substrate (chemistry), substrates, and the enzyme converts the substrates into different mol ...
s. For example, the most widely studied bacterium, ''E. coli'' strain K-12, is able to produce about 2,338 metabolic enzymes. These enzymes collectively form a complex web of reactions comprising pathways by which substrates (including nutients and intermediates) are converted to products (other intermediates and end-products).
The figure below shows a four step pathway, with intermediates, and . To sustain a steady-state, the boundary species and are fixed. Each step is catalyzed by an enzyme, .
Linear pathways follow a step-by-step sequence, where each enzymatic reaction results in the transformation of a substrate into an intermediate product. This intermediate is processed by subsequent enzymes until the final product is synthesized.
 A linear pathway can be studied in various ways. Multiple
A linear pathway can be studied in various ways. Multiple computer simulations
Computer simulation is the running of a mathematical model on a computer, the model being designed to represent the behaviour of, or the outcome of, a real-world or physical system. The reliability of some mathematical models can be determin ...
can be run to try to understand the pathway's behavior. Another way to understand the properties of a linear pathway is to take a more analytical approach. Analytical solutions can be derived for the steady-state if simple mass-action kinetics are assumed. Analytical solutions for the steady-state when assuming Michaelis-Menten kinetics can be obtained but are quite often avoided. Instead, such models are linearized. The three approaches that are usually used are therefore:
* Computer simulation
Computer simulation is the running of a mathematical model on a computer, the model being designed to represent the behaviour of, or the outcome of, a real-world or physical system. The reliability of some mathematical models can be determin ...
* Analytical solutions using a linear mathematical model
* Linearization
In mathematics, linearization (British English: linearisation) is finding the linear approximation to a function at a given point. The linear approximation of a function is the first order Taylor expansion around the point of interest. In the ...
of a non-linear
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathe ...
model
Computer simulation
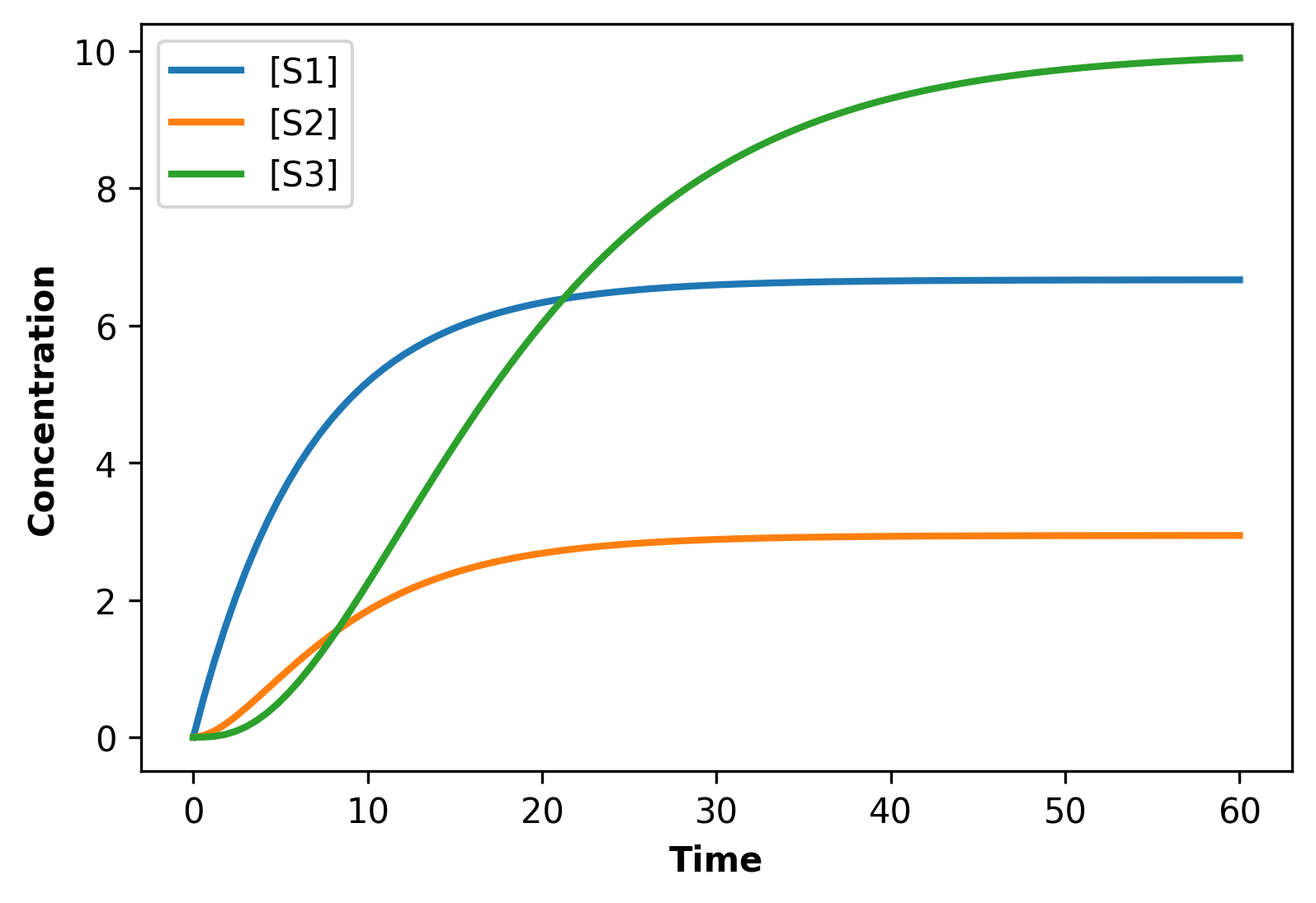
It is possible to build a computer simulation of a linear biochemical pathway. This can be done by building a simple model that describes each intermediate through a differential equation. The differential equations can be written by invoking mass conservation. For example, for the linear pathway: where and are fixed boundary species, the non-fixed intermediate can be described using the differential equation: The rate of change of the non-fixed intermediates and can be written in the same way: To run a simulation the rates, need to be defined. If mass-action kinetics are assumed for the reaction rates, then the differential equation can be written as: If values are assigned to the rate constants, , and the fixed species and the differential equations can be solved.
Analytical solutions
Computer simulations can only yield so much insight, as one would be required to run simulations on a wide range of parameter values, which can be unwieldy. A generally more powerful way to understand the properties of a model is to solve the differential equations analytically. Analytical solutions are possible if simple mass-action kinetics on each reaction step are assumed: : where and are the forward and reverse rate-constants, respectively. is the substrate and the product. If theequilibrium constant
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency ...
for this reaction is:
:
The mass-action kinetic equation can be modified to be:
:
Given the reaction rates, the differential equations describing the rates of change of the species can be described. For example, the rate of change of will equal:
:
By setting the differential equations to zero, the steady-state concentration for the species can be derived. From here, the pathway flux equation can be determined. For the three-step pathway, the steady-state concentrations of and are given by:
Inserting either or into one of the rate laws will give the steady-state pathway flux, :
:
A pattern can be seen in this equation such that, in general, for a linear pathway of steps, the steady-state pathway flux is given by:
Note that the pathway flux is a function of all the kinetic and thermodynamic parameters. This means there is no single parameter that determines the flux completely. If is equated to enzyme activity, then every enzyme in the pathway has some influence over the flux.
Linearized model: deriving control coefficients
Given the flux expression, it is possible to derive the flux control coefficients by differentiation and scaling of the flux expression. This can be done for the general case of steps: This result yields two corollaries: * The sum of the flux control coefficients is one. This confirms the summation theorem. * The value of an individual flux control coefficient in a linear reaction chain is greater than 0 or less than one: For the three-step linear chain, the flux control coefficients are given by: where is given by: Given these results, there are some patterns: * If all three steps have large equilibrium constants, that is , then tends to one and the remaining coefficients tend to zero. * If the equilibrium constants are smaller, control tends to get distributed across all three steps. With more moderate equilibrium constants, perturbations can travel upstream as well as downstream. For example, a perturbation at the last step, , is better able to influence the reaction rates upstream, which results in an alteration in the steady-state flux. An important result can be obtained if all are set as equal to each other. Under these conditions, the flux control coefficient is proportional to the numerator. That is: If it is assumed that the equilibrium constants are all greater than 1.0, as earlier steps have more terms, it must mean that earlier steps will, in general, have high larger flux control coefficients. In a linear chain of reaction steps, flux control will tend to be biased towards the front of the pathway. From a metabolic engineering or drug-targeting perspective, preference should be given to targeting the earlier steps in a pathway since they have the greatest effect on pathway flux. Note that this rule only applies to pathways without negative feedback loops.Heinrich R. and Schuster S. (1996) ''The Regulation of Cellular Systems'', Chapman and Hall.References
Metabolic pathways {{Improve categories, date=December 2023 Biochemistry Enzyme kinetics Metabolism