|
Kostant Partition Function
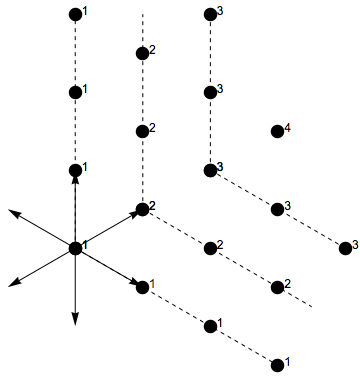
In representation theory, a branch of mathematics, the Kostant partition function, introduced by , of a root system \Delta is the number of ways one can represent a vector (weight) as a non-negative integer linear combination of the positive roots \Delta^+\subset\Delta. Kostant used it to rewrite the Weyl character formula as a formula (the Kostant multiplicity formula) for the multiplicity of a weight of an irreducible representation of a semisimple Lie algebra. An alternative formula, that is more computationally efficient in some cases, is Freudenthal's formula. The Kostant partition function can also be defined for Kac–Moody algebras and has similar properties. An example Consider the A2 root systems, with positive roots \alpha_1, \alpha_2, and \alpha_3:=\alpha_1+\alpha_2. If an element \mu can be expressed as a non-negative integer linear combination of \alpha_1, \alpha_2, and \alpha_3, then since \alpha_3=\alpha_1+\alpha_2, it can also be expressed as a non-negative int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weyl Character Formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by . There is a closely related formula for the character of an irreducible representation of a semisimple Lie algebra. In Weyl's approach to the representation theory of connected compact Lie groups, the proof of the character formula is a key step in proving that every dominant integral element actually arises as the highest weight of some irreducible representation. Important consequences of the character formula are the Weyl dimension formula and the Kostant multiplicity formula. By definition, the character \chi of a representation \pi of ''G'' is the trace of \pi(g), as a function of a group element g\in G. The irreducible representations in this case are all finite-dimensional (this is part of the Peter–Weyl theorem); so the notion of trace is the usual one from linear algebra. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representation Theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices and their algebraic operations (for example, matrix addition, matrix multiplication). The theory of matrices and linear operators is well-understood, so representations of more abstract objects in terms of familiar linear algebra objects helps glean properties and sometimes simplify calculations on more abstract theories. The algebraic objects amenable to such a description include groups, associative algebras and Lie algebras. The most prominent of these (and historically the first) is the representation theory of groups, in which elements of a group are represented by invertible matrices in such a way that the group operatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root System
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representation theory of semisimple Lie algebras. Since Lie groups (and some analogues such as algebraic groups) and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory (such as singularity theory). Finally, root systems are important for their own sake, as in spectral graph theory. Definitions and examples As a first example, consider the six vectors in 2-dimensional Euclidean space, R2, as shown in the image at the right; call them roots. These vectors span the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weight (representation Theory)
In the mathematical field of representation theory, a weight of an algebra ''A'' over a field F is an algebra homomorphism from ''A'' to F, or equivalently, a one-dimensional representation of ''A'' over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space. Motivation and general concept Given a set ''S'' of n\times n matrices over the same field, each of which is diagonalizable, and any two of which commute, it is always possible to simultaneously diagonalize all of the elements of ''S''.In fact, given a set of commuting matrices over an algebraically closed field, they are simultaneously triangularizable, without needing to assume that th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Root
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representation theory of semisimple Lie algebras. Since Lie groups (and some analogues such as algebraic groups) and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory (such as singularity theory). Finally, root systems are important for their own sake, as in spectral graph theory. Definitions and examples As a first example, consider the six vectors in 2-dimensional Euclidean space, R2, as shown in the image at the right; call them roots. These vectors span the wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial has a root at a given point is the multiplicity of that root. The notion of multiplicity is important to be able to count correctly without specifying exceptions (for example, ''double roots'' counted twice). Hence the expression, "counted with multiplicity". If multiplicity is ignored, this may be emphasized by counting the number of ''distinct'' elements, as in "the number of distinct roots". However, whenever a set (as opposed to multiset) is formed, multiplicity is automatically ignored, without requiring use of the term "distinct". Multiplicity of a prime factor In prime factorization, the multiplicity of a prime factor is its p-adic valuation. For example, the prime factorization of the integer is : the multiplicity of the prime factor is , while the multiplicity of each of the prime factors and i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irreducible Representation
In mathematics, specifically in the representation theory of groups and algebras, an irreducible representation (\rho, V) or irrep of an algebraic structure A is a nonzero representation that has no proper nontrivial subrepresentation (\rho, _W,W), with W \subset V closed under the action of \. Every finite-dimensional unitary representation on a Hilbert space V is the direct sum of irreducible representations. Irreducible representations are always indecomposable (i.e. cannot be decomposed further into a direct sum of representations), but converse may not hold, e.g. the two-dimensional representation of the real numbers acting by upper triangular unipotent matrices is indecomposable but reducible. History Group representation theory was generalized by Richard Brauer from the 1940s to give modular representation theory, in which the matrix operators act on a vector space over a field K of arbitrary characteristic, rather than a vector space over the field of real num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semisimple Lie Algebra
In mathematics, a Lie algebra is semisimple if it is a direct sum of simple Lie algebras. (A simple Lie algebra is a non-abelian Lie algebra without any non-zero proper ideals). Throughout the article, unless otherwise stated, a Lie algebra is a finite-dimensional Lie algebra over a field of characteristic 0. For such a Lie algebra \mathfrak g, if nonzero, the following conditions are equivalent: *\mathfrak g is semisimple; *the Killing form, κ(x,y) = tr(ad(''x'')ad(''y'')), is non-degenerate; *\mathfrak g has no non-zero abelian ideals; *\mathfrak g has no non-zero solvable ideals; * the radical (maximal solvable ideal) of \mathfrak g is zero. Significance The significance of semisimplicity comes firstly from the Levi decomposition, which states that every finite dimensional Lie algebra is the semidirect product of a solvable ideal (its radical) and a semisimple algebra. In particular, there is no nonzero Lie algebra that is both solvable and semisimple. Semisimple Li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kac–Moody Algebra
In mathematics, a Kac–Moody algebra (named for Victor Kac and Robert Moody, who independently and simultaneously discovered them in 1968) is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system, irreducible representations, and connection to flag manifolds have natural analogues in the Kac–Moody setting. A class of Kac–Moody algebras called affine Lie algebras is of particular importance in mathematics and theoretical physics, especially two-dimensional conformal field theory and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, the Macdonald identities, which is based on the representation theory of affine Kac–Moody algebras. Howard Garland and James Lepowsky demonstr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kostant Partition Function For A2
Bertram Kostant (May 24, 1928 – February 2, 2017) was an American mathematician who worked in representation theory, differential geometry, and mathematical physics. Early life and education Kostant grew up in New York City, where he graduated from Stuyvesant High School in 1945. He went on to obtain an undergraduate degree in mathematics from Purdue University in 1950. He earned his Ph.D. from the University of Chicago in 1954, under the direction of Irving Segal, where he wrote a dissertation on representations of Lie groups. Career in mathematics After time at the Institute for Advanced Study, Princeton University, and the University of California, Berkeley, he joined the faculty at the Massachusetts Institute of Technology, where he remained until his retirement in 1993. Kostant's work has involved representation theory, Lie groups, Lie algebras, homogeneous spaces, differential geometry and mathematical physics, particularly symplectic geometry. He has giv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Verma Module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics. Verma modules can be used in the classification of irreducible representations of a complex semisimple Lie algebra. Specifically, although Verma modules themselves are infinite dimensional, quotients of them can be used to construct finite-dimensional representations with highest weight \lambda, where \lambda is dominant and integral. Their homomorphisms correspond to invariant differential operators over flag manifolds. Informal construction We can explain the idea of a Verma module as follows. Let \mathfrak be a semisimple Lie algebra (over \mathbb, for simplicity). Let \mathfrak be a fixed Cartan subalgebra of \mathfrak and let R be the associated root system. Let R^+ be a fixed set of positive roots. For each \alpha\in R^+, choose a nonzero element X_\alpha for the corresponding root space \mathfrak_\alpha and a nonzero element Y_\alpha in the root ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.png)
