Kostant Partition Function on:
[Wikipedia]
[Google]
[Amazon]
In
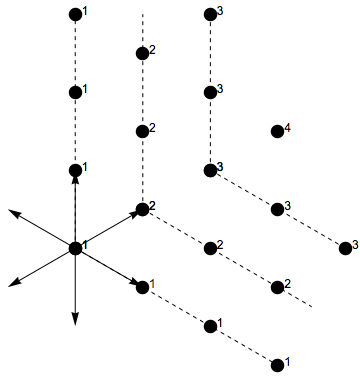 Consider the A2 root systems, with positive roots , , and . If an element can be expressed as a non-negative integer linear combination of , , and , then since , it can also be expressed as a non-negative integer linear combination of and :
:
with and being non-negative integers. This expression gives ''one'' way to write as a non-negative integer combination of positive roots; other expressions can be obtained by replacing with some number of times. We can do the replacement times, where . Thus, if the Kostant partition function is denoted by , we obtain the formula
:.
This result is shown graphically in the image at right. If an element is not of the form , then .
Consider the A2 root systems, with positive roots , , and . If an element can be expressed as a non-negative integer linear combination of , , and , then since , it can also be expressed as a non-negative integer linear combination of and :
:
with and being non-negative integers. This expression gives ''one'' way to write as a non-negative integer combination of positive roots; other expressions can be obtained by replacing with some number of times. We can do the replacement times, where . Thus, if the Kostant partition function is denoted by , we obtain the formula
:.
This result is shown graphically in the image at right. If an element is not of the form , then .
representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essen ...
, a branch of mathematics, the Kostant partition function, introduced by , of a root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representat ...
is the number of ways one can represent a vector (weight
In science and engineering, the weight of an object is the force acting on the object due to gravity.
Some standard textbooks define weight as a vector quantity, the gravitational force acting on the object. Others define weight as a scalar q ...
) as a non-negative integer linear combination of the positive root
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representatio ...
s . Kostant used it to rewrite the Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by . There is a closely related formula for the char ...
as a formula (the Kostant multiplicity formula) for the multiplicity of a weight of an irreducible representation of a semisimple Lie algebra
In mathematics, a Lie algebra is semisimple if it is a direct sum of simple Lie algebras. (A simple Lie algebra is a non-abelian Lie algebra without any non-zero proper ideals).
Throughout the article, unless otherwise stated, a Lie algebra is ...
. An alternative formula, that is more computationally efficient in some cases, is Freudenthal's formula.
The Kostant partition function can also be defined for Kac–Moody algebra
In mathematics, a Kac–Moody algebra (named for Victor Kac and Robert Moody, who independently and simultaneously discovered them in 1968) is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a ...
s and has similar properties.
An example
 Consider the A2 root systems, with positive roots , , and . If an element can be expressed as a non-negative integer linear combination of , , and , then since , it can also be expressed as a non-negative integer linear combination of and :
:
with and being non-negative integers. This expression gives ''one'' way to write as a non-negative integer combination of positive roots; other expressions can be obtained by replacing with some number of times. We can do the replacement times, where . Thus, if the Kostant partition function is denoted by , we obtain the formula
:.
This result is shown graphically in the image at right. If an element is not of the form , then .
Consider the A2 root systems, with positive roots , , and . If an element can be expressed as a non-negative integer linear combination of , , and , then since , it can also be expressed as a non-negative integer linear combination of and :
:
with and being non-negative integers. This expression gives ''one'' way to write as a non-negative integer combination of positive roots; other expressions can be obtained by replacing with some number of times. We can do the replacement times, where . Thus, if the Kostant partition function is denoted by , we obtain the formula
:.
This result is shown graphically in the image at right. If an element is not of the form , then .
Relation to the Weyl character formula
Inverting the Weyl denominator
For each root and each , we can ''formally'' apply the formula for the sum of a geometric series to obtain : where we do not worry about convergence—that is, the equality is understood at the level of formal power series. Using Weyl's denominator formula : we obtain a formal expression for the reciprocal of the Weyl denominator: : Here, the first equality is by taking a product over the positive roots of the geometric series formula and the second equality is by counting all the ways a given exponential can occur in the product.Rewriting the character formula
This argument shows that we can convert theWeyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by . There is a closely related formula for the char ...
for the irreducible representation with highest weight :
:
from a quotient to a product:
:
The multiplicity formula
Using the preceding rewriting of the character formula, it is relatively easy to write the character as a sum of exponentials. The coefficients of these exponentials are the multiplicities of the corresponding weights. We thus obtain a formula for the multiplicity of a given weight in the irreducible representation with highest weight : Theorem 10.29 :. This result is the Kostant multiplicity formula. The dominant term in this formula is the term ; the contribution of this term is , which is just the multiplicity of in theVerma module Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.
Verma modules can be used in the classification of irreducible representations of a complex semisimple Lie algebra. Sp ...
with highest weight . If is sufficiently far inside the fundamental Weyl chamber and is sufficiently close to , it may happen that all other terms in the formula are zero. Specifically, unless is higher than , the value of the Kostant partition function on will be zero. Thus, although the sum is nominally over the whole Weyl group, in most cases, the number of nonzero terms is smaller than the order of the Weyl group.
References
Sources
* * Humphreys, J.E. Introduction to Lie algebras and representation theory, Springer, 1972. * * {{refend Representation theory Representation theory of Lie algebras Types of functions