|
Branched Flow
Branched flow refers to a phenomenon in wave dynamics, that produces a tree-like pattern involving successive mostly forward scattering events by smooth obstacles deflecting traveling rays or waves. Sudden and significant momentum or wavevector changes are absent, but accumulated small changes can lead to large momentum changes. The path of a single ray is less important than the environs around a ray, which rotate, compress, and stretch around in an area preserving way. Even more revealing are groups, or manifolds of neighboring rays extending over significant zones. Starting rays out from a point but varying their direction over a range, one to the next, or from different points along a line all with the same initial directions are examples of a manifold. Waves have analogous launching conditions, such as a point source spraying in many directions, or an extended plane wave heading on one direction. The ray bending or refraction leads to characteristic structure in phase space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexural Rigidity
Flexural rigidity is defined as the force couple required to bend a fixed non- rigid structure by one unit of curvature, or as the resistance offered by a structure while undergoing bending. Flexural rigidity of a beam Although the moment M(x) and displacement y may vary along the length of the beam or rod, the flexural rigidity (defined as EI) is a property of the beam itself and is generally constant. The flexural rigidity, moment, and transverse displacement are related by the following equation along the length of the rod, x: :\ EI \ = \int_^ M(x) dx + C_1 where E is the flexural modulus (in Pa), I is the second moment of area (in m4), y is the transverse displacement of the beam at x, and M(x) is the bending moment at ''x''. The flexural rigidity (stiffness) of the beam is therefore related to both E, a material property, and I, the physical geometry of the beam. If the material exhibits Isotropic behavior then the Flexural Modulus is equal to the Modulus of Elasticity (Youn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Propagation
Wave propagation is any of the ways in which waves travel. Single wave propagation can be calculated by 2nd order wave equation ( standing wavefield) or 1st order one-way wave equation. With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves. For electromagnetic waves, propagation may occur in a vacuum as well as in the material medium. Other wave types cannot propagate through a vacuum and need a transmission medium to exist. Reflection of plane waves in a half-space The propagation and reflection of plane waves—e.g. Pressure waves (P-wave) or Shear waves (SH or SV-waves) are phenomena that were first characterized within the field of classical seismology, and are now considered fundamental concepts in modern seismic tomography. The analytical solution to this problem exists and is well known. The frequency domain solution can be obtained by first finding the Helmholtz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiclassical Physics
Semiclassical physics, or simply semiclassical refers to a theory in which one part of a system is described quantum mechanically whereas the other is treated classically. For example, external fields will be constant, or when changing will be classically described. In general, it incorporates a development in powers of Planck's constant, resulting in the classical physics of power 0, and the first nontrivial approximation to the power of (−1). In this case, there is a clear link between the quantum-mechanical system and the associated semi-classical and classical approximations, as it is similar in appearance to the transition from physical optics to geometric optics. Instances Some examples of a semiclassical approximation include: * WKB approximation: electrons in classical external electromagnetic fields. * semiclassical gravity: quantum field theory within a classical curved gravitational background (see general relativity). * quantum chaos; quantization of clas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rogue Wave
Rogue waves (also known as freak waves, monster waves, episodic waves, killer waves, extreme waves, and abnormal waves) are unusually large, unpredictable, and suddenly appearing surface waves that can be extremely dangerous to ships, even to large ones. They are distinct from tsunamis, which are often almost unnoticeable in deep waters and are caused by the displacement of water due to other phenomena (such as earthquakes). A rogue wave appearing at the shore is sometimes referred to as a sneaker wave. In oceanography, rogue waves are more precisely defined as waves whose height is more than twice the significant wave height (''H'' or SWH), which is itself defined as the mean of the largest third of waves in a wave record. Therefore, rogue waves are not necessarily the biggest waves found on the water; they are, rather, unusually large waves for a given sea state. Rogue waves seem not to have a single distinct cause, but occur where physical factors such as high winds and stro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chaos
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is: "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle states that classical mechanics is the classical limit of quantum mechanics, specifically in the limit as the ratio of Planck's constant to the action of the system tends to zero. If this is true, then there must be quantum mechanisms underlying classical chaos (although this may not be a fruitful way of examining classical chaos). If quantum mechanics does not demonstrate an exponential sensitivity to initial conditions, how can exponential sensitivity to initial conditions arise in classical chaos, which must be the correspondence principle limit of quantum mechanics?''Quantum Signatures of Chaos'', Fritz Haake, Edition: 2, Springer, 2001, , . Michael Berry, "Quantum Chaology", p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
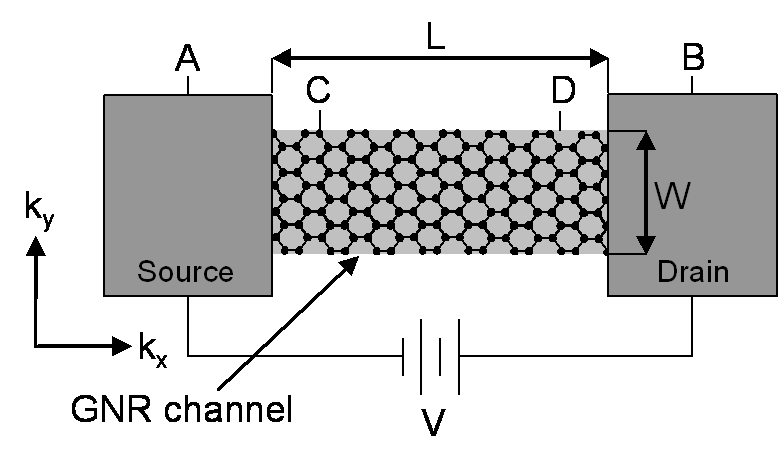
Ballistic Conduction
In mesoscopic physics, ballistic conduction (ballistic transport) is the unimpeded flow (or transport) of charge carriers (usually electrons), or energy-carrying particles, over relatively long distances in a material. In general, the resistivity of a material exists because an electron, while moving inside a medium, is scattered by impurities, defects, thermal fluctuations of ions in a crystalline solid, or, generally, by any freely-moving atom/molecule composing a gas or liquid. Without scattering, electrons simply obey Newton's second law of motion at non-relativistic speeds. The mean free path of a particle can be described as the average length that the particle can travel freely, i.e., before a collision, which could change its momentum. The mean free path can be increased by reducing the number of impurities in a crystal or by lowering its temperature. Ballistic transport is observed when the mean free path of the particle is (much) longer than the dimension of the med ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Caustic (optics)
In optics, a caustic or caustic network is the Envelope (mathematics), envelope of Ray (optics), light rays which have been Reflection (physics), reflected or refraction, refracted by a curved surface or object, or the Projection (mathematics), projection of that envelope of rays on another surface. The caustic is a curve or Surface (mathematics), surface to which each of the light rays is tangent, defining a boundary of an envelope of rays as a curve of concentrated light. Therefore, in the photo to the right, caustics can be seen as patches of light or their bright edges. These shapes often have cusp (singularity), cusp singularities. Explanation Concentration of light, especially sunlight, can burn. The word ''caustic'', in fact, comes from the Greek καυστός, burnt, via the Latin ''causticus'', burning. A common situation where caustics are visible is when light shines on a drinking glass. The glass casts a shadow, but also produces a curved region of bright li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catastrophe Theory
In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry. Bifurcation theory studies and classifies phenomena characterized by sudden shifts in behavior arising from small changes in circumstances, analysing how the qualitative nature of equation solutions depends on the parameters that appear in the equation. This may lead to sudden and dramatic changes, for example the unpredictable timing and magnitude of a landslide. Catastrophe theory originated with the work of the French mathematician René Thom in the 1960s, and became very popular due to the efforts of Christopher Zeeman in the 1970s. It considers the special case where the long-run stable equilibrium can be identified as the minimum of a smooth, well-defined potential function ( Lyapunov function). In the late 1970s, applications of catastrophe theory to areas outside its scope began ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeldovich Pancake
A Zel'dovich pancake is a theoretical condensation of gas out of a primordial density fluctuation following the Big Bang. In 1970, Yakov B. Zel'dovich showed that for an ellipsoid of gas on a supergalactic scale, an approximation can be used that will model the collapse as occurring most rapidly along the shortest axis, resulting in a pancake form. This approximation assumes that the ellipsoid of gas is sufficiently large that the effect of pressure is negligible and only gravitational attraction needs to be considered. That is, the gas will collapse without being significantly perturbed by outward pressure. This assumption is especially valid if the collapse occurs before the recombination era that resulted in the formation of hydrogen atoms. In 1989, Zel'dovich and S. F. Shandarin showed that initial overlapping density fluctuations of random Gaussian fields would result in "dense pancakes, filaments, and compact clumps of matter". This model became known as a top-down model of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plate (structure)
A plate is a structural element which is characterized by a three-dimensional solid whose thickness is very small when compared with other dimensions. The effects of the loads that are expected to be applied on it only generate stresses whose resultants are, in practical terms, exclusively normal to the element's thickness. Their mechanics are the main subject of the plate theory. Thin plates are initially flat structural members bounded by two parallel planes, called faces, and a cylindrical surface, called an edge or boundary. The generators of the cylindrical surface are perpendicular to the plane faces. The distance between the plane faces is called the thickness (h) of the plate. It will be assumed that the plate thickness is small compared with other characteristic dimensions of the faces (length, width, diameter, etc.). Geometrically, plates are bounded either by straight or curved boundaries. The static or dynamic loads carried by plates are predominantly perpendicular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |