|
AM–GM Inequality
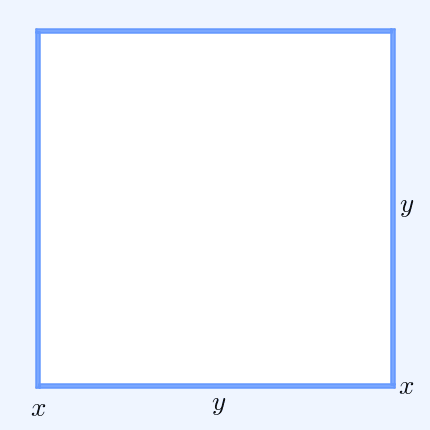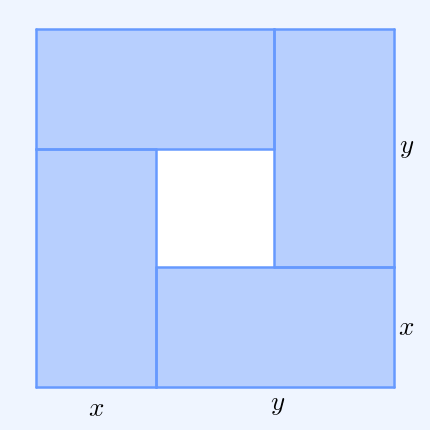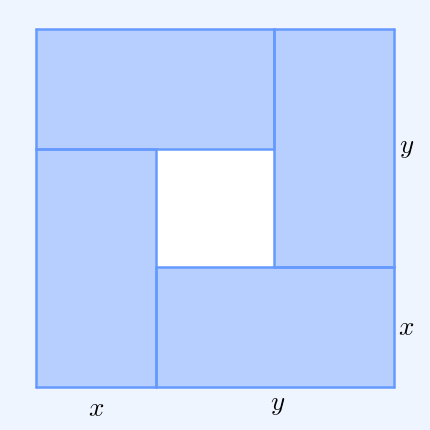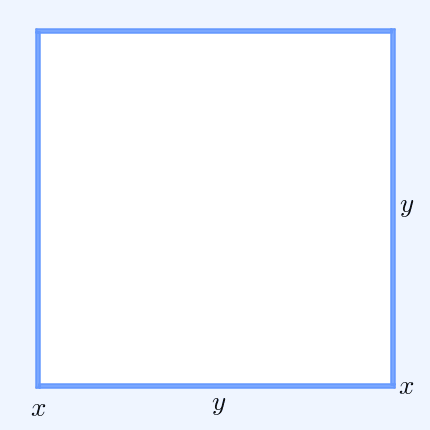
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same (in which case they are both that number). The simplest non-trivial case is for two non-negative numbers and , that is, :\frac2 \ge \sqrt with equality if and only if . This follows from the fact that the square of a real number is always non-negative (greater than or equal to zero) and from the identity : :\begin 0 & \le (x-y)^2 \\ & = x^2-2xy+y^2 \\ & = x^2+2xy+y^2 - 4xy \\ & = (x+y)^2 - 4xy. \end For a geometrical interpretation, consider a rectangle with sides of length and ; it has perimeter and area . Similarly, a square with all sides of length has the perimeter and the same area as the rectangle. The simplest non-tri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
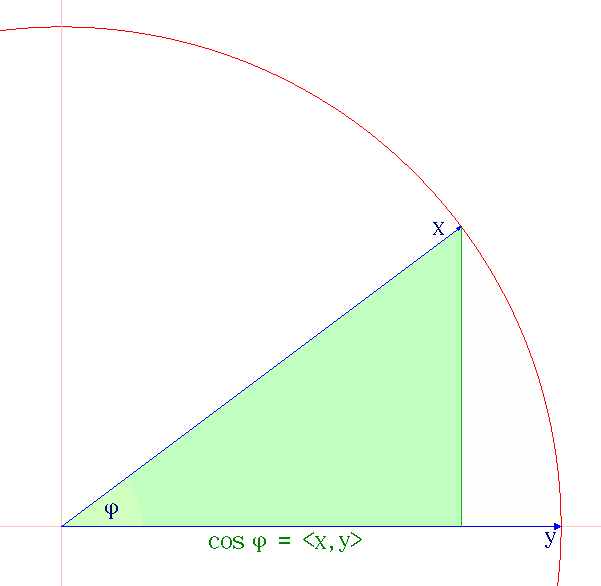
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the absolute value of the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics. Inner products of vectors can describe finite sums (via finite-dimensional vector spaces), infinite series (via vectors in sequence spaces), and integrals (via vectors in Hilbert spaces). The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Calculus
In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve. The primary objects of study in differential calculus are the derivative of a Function (mathematics), function, related notions such as the Differential of a function, differential, and their applications. The derivative of a function at a chosen input value describes the Rate (mathematics)#Of_change, rate of change of the function near that input value. The process of finding a derivative is called differentiation. Geometrically, the derivative at a point is the slope of the tangent, tangent line to the graph of a function, graph of the function at that point, provided that the derivative exists and is defined at that point. For a real-valued function of a single real variable, the derivative of a function at a point generally determines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy ( , , ; ; 21 August 1789 – 23 May 1857) was a French mathematician, engineer, and physicist. He was one of the first to rigorously state and prove the key theorems of calculus (thereby creating real analysis), pioneered the field complex analysis, and the study of permutation groups in abstract algebra. Cauchy also contributed to a number of topics in mathematical physics, notably continuum mechanics. A profound mathematician, Cauchy had a great influence over his contemporaries and successors; Hans Freudenthal stated: : "More concepts and theorems have been named for Cauchy than for any other mathematician (in elasticity alone there are sixteen concepts and theorems named for Cauchy)." Cauchy was a prolific worker; he wrote approximately eight hundred research articles and five complete textbooks on a variety of topics in the fields of mathematics and mathematical physics. Biography Youth and education Cauchy was the son of Louis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Induction
Mathematical induction is a method for mathematical proof, proving that a statement P(n) is true for every natural number n, that is, that the infinitely many cases P(0), P(1), P(2), P(3), \dots all hold. This is done by first proving a simple case, then also showing that if we assume the claim is true for a given case, then the next case is also true. Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder: A proof by induction consists of two cases. The first, the base case, proves the statement for n = 0 without assuming any knowledge of other cases. The second case, the induction step, proves that ''if'' the statement holds for any given case n = k, ''then'' it must also hold for the next case n = k + 1. These two steps establish that the statement holds for every natural number n. The base case does not necessarily begin with n = 0, but often with n = 1, and possibly with any fixed natural number n = N, establishing the trut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antilog
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , then is the logarithm of to base , written , so . As a single-variable function, the logarithm to base is the inverse of exponentiation with base . The logarithm base is called the ''decimal'' or ''common'' logarithm and is commonly used in science and engineering. The ''natural'' logarithm has the number as its base; its use is widespread in mathematics and physics because of its very simple derivative. The ''binary'' logarithm uses base and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written . Logarithms were introduced by John Napier in 1614 as a means of simplifying calculations. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concave Function
In mathematics, a concave function is one for which the function value at any convex combination of elements in the domain is greater than or equal to that convex combination of those domain elements. Equivalently, a concave function is any function for which the hypograph is convex. The class of concave functions is in a sense the opposite of the class of convex functions. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex. Definition A real-valued function f on an interval (or, more generally, a convex set in vector space) is said to be ''concave'' if, for any x and y in the interval and for any \alpha \in ,1/math>, :f((1-\alpha )x+\alpha y)\geq (1-\alpha ) f(x)+\alpha f(y) A function is called ''strictly concave'' if :f((1-\alpha )x+\alpha y) > (1-\alpha ) f(x)+\alpha f(y) for any \alpha \in (0,1) and x \neq y. For a function f: \mathbb \to \mathbb, this second definition merely states that for ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jensen's Inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation (or equivalently, the opposite inequality for concave transformations). Jensen's inequality generalizes the statement that the secant line of a convex function lies ''above'' the graph of the function, which is Jensen's inequality for two points: the secant line consists of weighted means of the convex function (for ''t'' ∈ ,1, :t f(x_1) + (1-t) f(x_2), while the g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial SOS
In mathematics, a form (i.e. a homogeneous polynomial) ''h''(''x'') of degree 2''m'' in the real ''n''-dimensional vector ''x'' is sum of squares of forms (SOS) if and only if there exist forms g_1(x),\ldots,g_k(x) of degree ''m'' such that h(x) = \sum_^k g_i(x)^2 . Every form that is SOS is also a positive polynomial, and although the converse is not always true, Hilbert proved that for ''n'' = 2, 2''m'' = 2, or ''n'' = 3 and 2''m'' = 4 a form is SOS if and only if it is positive. The same is also valid for the analog problem on positive ''symmetric'' forms. Although not every form can be represented as SOS, explicit sufficient conditions for a form to be SOS have been found. Moreover, every real nonnegative form can be approximated as closely as desired (in the l_1-norm of its coefficient vector) by a sequence of forms \ that are SOS. Square matricial representation (SMR) To establish whether a form is SOS amounts to solving a convex optimization problem. Indeed, any ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonnegative Polynomial
In mathematics, a positive polynomial (respectively non-negative polynomial) on a particular set (mathematics), set is a polynomial whose values are positive (respectively non-negative) on that set. Precisely, Let p be a polynomial in n variables with real number, real coefficients and let S be a subset of the n-dimensional Euclidean space \mathbb^n. We say that: * p is positive on S if p(x)>0 for every x in S. * p is non-negative on S if p(x)\ge 0 for every x in S. Positivstellensatz (and nichtnegativstellensatz) For certain sets S, there exist algebraic descriptions of all polynomials that are positive (resp. non-negative) on S. Such a description is a positivstellensatz (resp. nichtnegativstellensatz). The importance of Positivstellensatz theorems in computation arises from its ability to transform problems of polynomial optimization into semidefinite programming problems, which can be efficiently solved using convex optimization techniques. Examples of positivstellensatz ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |