|
3-space
In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane (a tangent plane) to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below. Principles Definition A topological space M is a 3-manifold if it is a second-countable Hausdorff space and if every point in M has a neighbourhood that is homeomorphic to Euclidean 3-space. Mathematical theory of 3-manifolds The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds. Phenomena in three dimensions can be strikingly different from phenomena in other dimensions, and so there is a prevalence of very specialized techniques ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-Manifold 3-Torus
In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane (geometry), plane (a tangent plane) to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below. Principles Definition A topological space M is a 3-manifold if it is a second-countable Hausdorff space and if every point in M has a neighbourhood (mathematics), neighbourhood that is homeomorphic to Euclidean 3-space. Mathematical theory of 3-manifolds The topological, Piecewise linear manifold, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds. Phenomena in three dimensions can be strikingly different from phenomena in other dim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean 3-space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values (''coordinates'') are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called ''3-manifolds''. The term may also refer colloquially to a subset of space, a ''three-dimensional region'' (or 3D domain), a ''solid figure''. Technically, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the pair formed by a -dimensional Euclidean space and a Cartesian coordinate system. When , this space is called the three-dimensional Euclidean space (or simply "Euclidean space" when the context is clear). In classical physics, it serves as a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or János Bolyai, Bolyai–Nikolai Lobachevsky, Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For any given line ''R'' and point ''P'' not on ''R'', in the plane containing both line ''R'' and point ''P'' there are at least two distinct lines through ''P'' that do not intersect ''R''. (Compare the above with Playfair's axiom, the modern version of Euclid's parallel postulate.) The hyperbolic plane is a plane (mathematics), plane where every point is a saddle point. Hyperbolic plane geometry is also the geometry of pseudosphere, pseudospherical surfaces, surfaces with a constant negative Gaussian curvature. Saddle surfaces have negative Gaussian curvature in at least some regions, where they local property, locally resemble the hyperbolic plane. The hyperboloid model of hyperbolic geometry provides a representation of event (relativity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Euclidean Space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values (''coordinates'') are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called ''3-manifolds''. The term may also refer colloquially to a subset of space, a ''three-dimensional region'' (or 3D domain), a ''solid figure''. Technically, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the pair formed by a -dimensional Euclidean space and a Cartesian coordinate system. When , this space is called the three-dimensional Euclidean space (or simply "Euclidean space" when the context is clear). In classical physics, it serves as a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
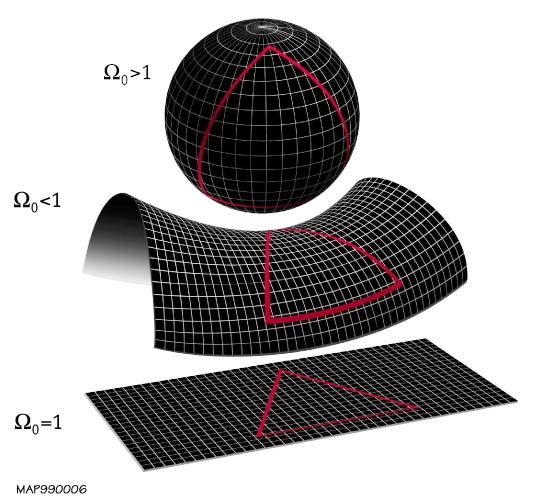
Shape Of The Universe
In physical cosmology, the shape of the universe refers to both its local and global geometry. Local geometry is defined primarily by its curvature, while the global geometry is characterised by its topology (which itself is constrained by curvature). General relativity explains how spatial curvature (local geometry) is constrained by gravity. The global topology of the universe cannot be deduced from measurements of curvature inferred from observations within the family of homogeneous general relativistic models alone, due to the existence of locally indistinguishable spaces with varying global topological characteristics. For example; a multiply connected space like a 3 torus has everywhere zero curvature but is finite in extent, whereas a flat simply connected space is infinite in extent (such as Euclidean space). Current observational evidence ( WMAP, BOOMERanG, and Planck for example) imply that the observable universe is spatially flat to within a 0.4% margin of error o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Theory
In topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram, in which any knot can be drawn in many different ways. Therefore, a fundamental p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a Neighbourhood (mathematics), neighborhood that is homeomorphic to an open (topology), open subset of n-dimensional Euclidean space. One-dimensional manifolds include Line (geometry), lines and circles, but not Lemniscate, self-crossing curves such as a figure 8. Two-dimensional manifolds are also called Surface (topology), surfaces. Examples include the Plane (geometry), plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Low-dimensional Topology
In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory. History A number of advances starting in the 1960s had the effect of emphasising low dimensions in topology. The solution by Stephen Smale, in 1961, of the Poincaré conjecture in five or more dimensions made dimensions three and four seem the hardest; and indeed they required new methods, while the freedom of higher dimensions meant that questions could be reduced to computational methods available in surgery theory. Thurston's geometrization conjecture, formulated in the late 1970s, offered a framework that suggeste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heegaard Splitting
In the mathematical field of geometric topology, a Heegaard splitting () is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies. Definitions Let ''V'' and ''W'' be handlebodies of genus ''g'', and let ƒ be an orientation reversing homeomorphism from the boundary of ''V'' to the boundary of ''W''. By gluing ''V'' to ''W'' along ƒ we obtain the compact oriented 3-manifold : M = V \cup_f W. Every closed, orientable three-manifold may be so obtained; this follows from deep results on the triangulability of three-manifolds due to Moise. This contrasts strongly with higher-dimensional manifolds which need not admit smooth or piecewise linear structures. Assuming smoothness the existence of a Heegaard splitting also follows from the work of Smale about handle decompositions from Morse theory. The decomposition of ''M'' into two handlebodies is called a Heegaard splitting, and their common boundary ''H'' is called the Heegaard su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Haken Manifold
In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface. Sometimes one considers only orientable Haken manifolds, in which case a Haken manifold is a compact, orientable, irreducible 3-manifold that contains an orientable, incompressible surface. A 3-manifold finitely covered by a Haken manifold is said to be virtually Haken. The Virtually Haken conjecture asserts that every compact, irreducible 3-manifold with infinite fundamental group is virtually Haken. This conjecture was proven by Ian Agol. Haken manifolds were introduced by . proved that Haken manifolds have a hierarchy, where they can be split up into 3-balls along incompressible surfaces. Haken also showed that there was a finite procedure to find an incompressible surface if the 3-manifold had one. gave an algorithm to determine if a 3-manifold was Haken. Normal surfaces are ubiquitous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incompressible Surface
In mathematics, an incompressible surface is a surface properly embedded in a 3-manifold, which, in intuitive terms, is a "nontrivial" surface that cannot be simplified. In non-mathematical terms, the surface of a suitcase is compressible, because we could cut the handle and shrink it into the surface. But a Conway sphere (a sphere with four holes) is incompressible, because there are essential parts of a knot or link both inside and out, so there is no way to move the entire knot or link to one side of the punctured sphere. The mathematical definition is as follows. There are two cases to consider. A sphere is incompressible if both inside and outside the sphere there are some obstructions that prevent the sphere from shrinking to a point and also prevent the sphere from expanding to encompass all of space. A surface other than a sphere is incompressible if any disk with its boundary on the surface spans a disk in the surface."An Introduction to Knot Theory", W. B. Raymond Lickoris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Quantum Field Theory
In gauge theory and mathematical physics, a topological quantum field theory (or topological field theory or TQFT) is a quantum field theory that computes topological invariants. While TQFTs were invented by physicists, they are also of mathematical interest, being related to, among other things, knot theory and the theory of four-manifolds in algebraic topology, and to the theory of moduli spaces in algebraic geometry. Donaldson, Jones, Witten, and Kontsevich have all won Fields Medals for mathematical work related to topological field theory. In condensed matter physics, topological quantum field theories are the low-energy effective theories of topologically ordered states, such as fractional quantum Hall states, string-net condensed states, and other strongly correlated quantum liquid states. Overview In a topological field theory, correlation functions do not depend on the metric of spacetime. This means that the theory is not sensitive to changes in the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |