Composite material on:
[Wikipedia]
[Google]
[Amazon]
 A composite or composite material (also composition material) is a
A composite or composite material (also composition material) is a

 Fibre-reinforced polymers include carbon-fiber-reinforced polymers and
Fibre-reinforced polymers include carbon-fiber-reinforced polymers and  A sandwich-structured composite is a special class of composite material that is fabricated by attaching two thin but stiff skins to a lightweight but thick core. The core material is normally low strength material, but its higher thickness provides the sandwich composite with high
A sandwich-structured composite is a special class of composite material that is fabricated by attaching two thin but stiff skins to a lightweight but thick core. The core material is normally low strength material, but its higher thickness provides the sandwich composite with high  Wood is a naturally occurring composite comprising cellulose fibres in a
Wood is a naturally occurring composite comprising cellulose fibres in a
 Composite materials are created from individual materials. These individual materials are known as constituent materials, and there are two main categories of it. One is the
Composite materials are created from individual materials. These individual materials are known as constituent materials, and there are two main categories of it. One is the
 Usually, the composite's physical properties are dependent on the direction of consideration, and so are
Usually, the composite's physical properties are dependent on the direction of consideration, and so are  For some material property , the rule of mixtures states that the overall property in the direction parallel to the fibers could be as high as
:
The inverse rule of mixtures states that in the direction
For some material property , the rule of mixtures states that the overall property in the direction parallel to the fibers could be as high as
:
The inverse rule of mixtures states that in the direction
 A composite or composite material (also composition material) is a
A composite or composite material (also composition material) is a material
A material is a matter, substance or mixture of substances that constitutes an Physical object, object. Materials can be pure or impure, living or non-living matter. Materials can be classified on the basis of their physical property, physical ...
which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a material with properties unlike the individual elements. Within the finished structure, the individual elements remain separate and distinct, distinguishing composites from mixture
In chemistry, a mixture is a material made up of two or more different chemical substances which can be separated by physical method. It is an impure substance made up of 2 or more elements or compounds mechanically mixed together in any proporti ...
s and solid solution
A solid solution, a term popularly used for metals, is a homogeneous mixture of two compounds in solid state and having a single crystal structure. Many examples can be found in metallurgy, geology, and solid-state chemistry. The word "solutio ...
s. Composite materials with more than one distinct layer are called '' composite laminates''.
Typical engineered composite materials
A material is a substance or mixture of substances that constitutes an object. Materials can be pure or impure, living or non-living matter. Materials can be classified on the basis of their physical and chemical properties, or on their ge ...
are made up of a binding agent forming the ''matrix'' and a filler material ( particulates or fibres) giving ''substance'', e.g.:
* Concrete
Concrete is a composite material composed of aggregate bound together with a fluid cement that cures to a solid over time. It is the second-most-used substance (after water), the most–widely used building material, and the most-manufactur ...
, reinforced concrete
Reinforced concrete, also called ferroconcrete or ferro-concrete, is a composite material in which concrete's relatively low tensile strength and ductility are compensated for by the inclusion of reinforcement having higher tensile strength or ...
and masonry
Masonry is the craft of building a structure with brick, stone, or similar material, including mortar plastering which are often laid in, bound, and pasted together by mortar (masonry), mortar. The term ''masonry'' can also refer to the buildin ...
with cement, lime or mortar (which is itself a composite material) as a binder
* Composite wood such as glulam and plywood with wood glue
Wood glue is an adhesive used to tightly bond pieces of wood together. Many substances have been used as glues. Traditionally animal proteins like casein from milk or collagen from animal hides and bones were boiled down to make early glues. They w ...
as a binder
* Reinforced plastics, such as fiberglass
Fiberglass (American English) or fibreglass (English in the Commonwealth of Nations, Commonwealth English) is a common type of fibre-reinforced plastic, fiber-reinforced plastic using glass fiber. The fibers may be randomly arranged, flattened i ...
and fibre-reinforced polymer with resin
A resin is a solid or highly viscous liquid that can be converted into a polymer. Resins may be biological or synthetic in origin, but are typically harvested from plants. Resins are mixtures of organic compounds, predominantly terpenes. Commo ...
or thermoplastic
A thermoplastic, or thermosoftening plastic, is any plastic polymer material that becomes pliable or moldable at a certain elevated temperature and solidifies upon cooling.
Most thermoplastics have a high molecular weight. The polymer chains as ...
s as a binder
* Ceramic matrix composites ( composite ceramic and metal matrices)
* Metal matrix composite
In materials science, a metal matrix composite (MMC) is a composite material with fibers or particles dispersed in a metallic matrix, such as copper, aluminum, or steel. The secondary phase is typically a ceramic (such as alumina or silicon carb ...
s
* advanced composite materials, often first developed for spacecraft
A spacecraft is a vehicle that is designed spaceflight, to fly and operate in outer space. Spacecraft are used for a variety of purposes, including Telecommunications, communications, Earth observation satellite, Earth observation, Weather s ...
and aircraft
An aircraft ( aircraft) is a vehicle that is able to flight, fly by gaining support from the Atmosphere of Earth, air. It counters the force of gravity by using either Buoyancy, static lift or the Lift (force), dynamic lift of an airfoil, or, i ...
applications.
Composite materials can be less expensive, lighter, stronger or more durable than common materials. Some are inspired by biological structures found in plants and animals.
Robotic materials are composites that include sensing, actuation, computation, and communication components.
Composite materials are used for construction
Construction are processes involved in delivering buildings, infrastructure, industrial facilities, and associated activities through to the end of their life. It typically starts with planning, financing, and design that continues until the a ...
and technical structure
A structure is an arrangement and organization of interrelated elements in a material object or system, or the object or system so organized. Material structures include man-made objects such as buildings and machines and natural objects such as ...
s such as boat hulls, swimming pool
A swimming pool, swimming bath, wading pool, paddling pool, or simply pool, is a structure designed to hold water to enable Human swimming, swimming and associated activities. Pools can be built into the ground (in-ground pools) or built abo ...
panels, racing car
Auto racing (also known as car racing, motor racing, or automobile racing) is a motorsport involving the racing of automobiles for competition. In North America, the term is commonly used to describe all forms of automobile sport including ...
bodies, shower
A shower is a place in which a person bathes under a spray of typically warm or hot water. Indoors, there is a drain in the floor. Most showers are set up to have adjustable temperature, spray pressure and showerhead nozzle angle. The si ...
stalls, bathtub
A bathtub, also known simply as a bath or tub, is a container for holding water in which a person or another animal may Bathing, bathe. Most modern bathtubs are made of thermoformed Acrylic resin, acrylic, porcelain enamel, porcelain-enameled s ...
s, storage tanks, imitation granite
Granite ( ) is a coarse-grained (phanerite, phaneritic) intrusive rock, intrusive igneous rock composed mostly of quartz, alkali feldspar, and plagioclase. It forms from magma with a high content of silica and alkali metal oxides that slowly coo ...
, and cultured marble sink
A sink (also known as ''basin'' in the UK) is a bowl-shaped plumbing fixture for washing hands, dishwashing, and other purposes. Sinks have a tap (faucet) that supplies hot and cold water and may include a spray feature to be used for fas ...
s and countertops. They are also being increasingly used in general automotive applications.
History
The earliest composite materials were made fromstraw
Straw is an agricultural byproduct consisting of the dry wikt:stalk, stalks of cereal plants after the grain and chaff have been removed. It makes up about half of the crop yield, yield by weight of cereal crops such as barley, oats, rice, ry ...
and mud combined to form brick
A brick is a type of construction material used to build walls, pavements and other elements in masonry construction. Properly, the term ''brick'' denotes a unit primarily composed of clay. But is now also used informally to denote building un ...
s for building
A building or edifice is an enclosed Structure#Load-bearing, structure with a roof, walls and window, windows, usually standing permanently in one place, such as a house or factory. Buildings come in a variety of sizes, shapes, and functions, a ...
construction
Construction are processes involved in delivering buildings, infrastructure, industrial facilities, and associated activities through to the end of their life. It typically starts with planning, financing, and design that continues until the a ...
. Ancient brick-making was documented by Egyptian tomb paintings.
Wattle and daub
Wattle and daub is a composite material, composite building method in which a woven lattice of wooden strips called "wattle (construction), wattle" is "daubed" with a sticky material usually made of some combination of wet soil, clay, sand, and ...
might be the oldest composite materials, at over 6000 years old.
* Woody plant
Plants are the eukaryotes that form the Kingdom (biology), kingdom Plantae; they are predominantly Photosynthesis, photosynthetic. This means that they obtain their energy from sunlight, using chloroplasts derived from endosymbiosis with c ...
s, both true wood
Wood is a structural tissue/material found as xylem in the stems and roots of trees and other woody plants. It is an organic materiala natural composite of cellulosic fibers that are strong in tension and embedded in a matrix of lignin t ...
from trees and such plants as palms and bamboo
Bamboos are a diverse group of mostly evergreen perennial plant, perennial flowering plants making up the subfamily (biology), subfamily Bambusoideae of the grass family Poaceae. Giant bamboos are the largest members of the grass family, in th ...
, yield natural composites that were used prehistorically by humankind and are still used widely in construction and scaffolding.
* Plywood, 3400 BC, by the Ancient Mesopotamians; gluing wood at different angles gives better properties than natural wood.
* Cartonnage, layers of linen
Linen () is a textile made from the fibers of the flax plant.
Linen is very strong and absorbent, and it dries faster than cotton. Because of these properties, linen is comfortable to wear in hot weather and is valued for use in garments. Lin ...
or papyrus
Papyrus ( ) is a material similar to thick paper that was used in ancient times as a writing surface. It was made from the pith of the papyrus plant, ''Cyperus papyrus'', a wetland sedge. ''Papyrus'' (plural: ''papyri'' or ''papyruses'') can a ...
soaked in plaster dates to the First Intermediate Period of Egypt c. 2181–2055 BC and was used for death masks.
* Cob mud bricks, or mud walls, (using mud (clay) with straw or gravel as a binder) have been used for thousands of years.
* Concrete
Concrete is a composite material composed of aggregate bound together with a fluid cement that cures to a solid over time. It is the second-most-used substance (after water), the most–widely used building material, and the most-manufactur ...
was described by Vitruvius
Vitruvius ( ; ; –70 BC – after ) was a Roman architect and engineer during the 1st century BC, known for his multi-volume work titled . As the only treatise on architecture to survive from antiquity, it has been regarded since the Renaissan ...
, writing around 25 BC in his ''Ten Books on Architecture'', distinguished types of aggregate appropriate for the preparation of lime mortar
Lime mortar or torching is a masonry mortar (masonry), mortar composed of lime (material), lime and an construction aggregate, aggregate such as sand, mixed with water. It is one of the oldest known types of mortar, used in ancient Rome and anci ...
s. For ''structural mortars'', he recommended ''pozzolana
Pozzolana or pozzuolana ( , ), also known as pozzolanic ash (), is a natural siliceous or siliceous- aluminous material which reacts with calcium hydroxide in the presence of water at room temperature (cf. pozzolanic reaction). In this reaction ...
'', which were volcanic sands from the sandlike beds of Pozzuoli brownish-yellow-gray in colour near Naples
Naples ( ; ; ) is the Regions of Italy, regional capital of Campania and the third-largest city of Italy, after Rome and Milan, with a population of 908,082 within the city's administrative limits as of 2025, while its Metropolitan City of N ...
and reddish-brown at Rome
Rome (Italian language, Italian and , ) is the capital city and most populated (municipality) of Italy. It is also the administrative centre of the Lazio Regions of Italy, region and of the Metropolitan City of Rome. A special named with 2, ...
. Vitruvius specifies a ratio of 1 part lime to 3 parts pozzolana for cements used in buildings and a 1:2 ratio of lime to pulvis Puteolanus for underwater work, essentially the same ratio mixed today for concrete used at sea. Natural cement-stones, after burning, produced cements used in concretes from post-Roman times into the 20th century, with some properties superior to manufactured Portland cement
Portland cement is the most common type of cement in general use around the world as a basic ingredient of concrete, mortar (masonry), mortar, stucco, and non-specialty grout. It was developed from other types of hydraulic lime in England in th ...
.
* Papier-mâché
file:JacmelMardiGras.jpg, upright=1.3, Mardi Gras papier-mâché masks, Haiti
Papier-mâché ( , , - the French term "mâché" here means "crushed and ground") is a versatile craft technique with roots in ancient China, in which waste paper is s ...
, a composite of paper and glue, has been used for hundreds of years.
* The first artificial fibre reinforced plastic was a combination of fiber glass and bakelite
Bakelite ( ), formally , is a thermosetting polymer, thermosetting phenol formaldehyde resin, formed from a condensation reaction of phenol with formaldehyde. The first plastic made from synthetic components, it was developed by Belgian chemist ...
, performed in 1935 by Al Simison and Arthur D Little in Owens Corning Company
* One of the most common and familiar composite is fibreglass, in which small glass fibre are embedded within a polymeric material (normally an epoxy or polyester). The glass fibre is relatively strong and stiff (but also brittle), whereas the polymer is ductile (but also weak and flexible). Thus the resulting fibreglass is relatively stiff, strong, flexible, and ductile.
* Composite bow
A composite bow is a traditional bow made from horn, wood, and sinew laminated together, a form of laminated bow. The horn is on the belly, facing the archer, and sinew on the outer side of a wooden core. When the bow is drawn, the sinew (s ...
* Leather cannon, wooden cannon
Examples
Composite materials
Concrete
Concrete is a composite material composed of aggregate bound together with a fluid cement that cures to a solid over time. It is the second-most-used substance (after water), the most–widely used building material, and the most-manufactur ...
is the most common artificial composite material of all. , about 7.5 billion cubic metres of concrete are made each year.
Concrete typically consists of loose stones ( construction aggregate) held with a matrix of cement
A cement is a binder, a chemical substance used for construction that sets, hardens, and adheres to other materials to bind them together. Cement is seldom used on its own, but rather to bind sand and gravel ( aggregate) together. Cement mi ...
. Concrete is an inexpensive material resisting large compressive forces, however, susceptible to tensile loading. To give concrete the ability to resist being stretched, steel bars, which can resist high stretching (tensile) forces, are often added to concrete to form reinforced concrete
Reinforced concrete, also called ferroconcrete or ferro-concrete, is a composite material in which concrete's relatively low tensile strength and ductility are compensated for by the inclusion of reinforcement having higher tensile strength or ...
.
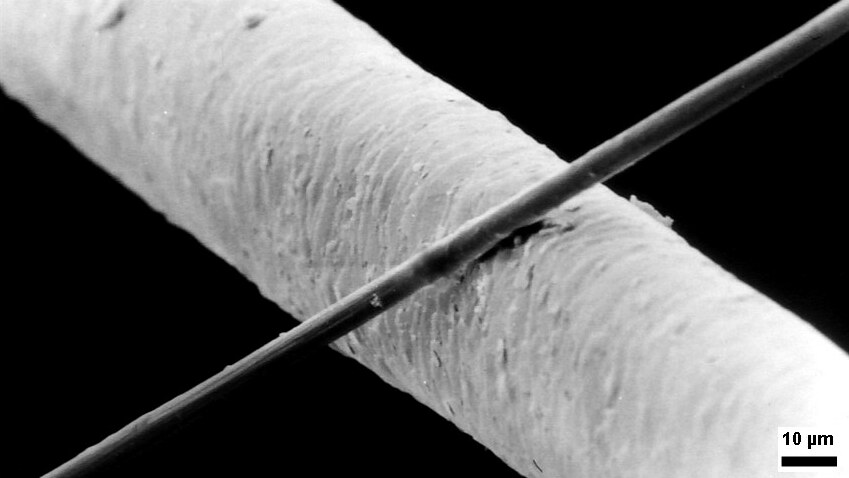
 Fibre-reinforced polymers include carbon-fiber-reinforced polymers and
Fibre-reinforced polymers include carbon-fiber-reinforced polymers and glass-reinforced plastic
Fiberglass (American English) or fibreglass ( Commonwealth English) is a common type of fiber-reinforced plastic using glass fiber. The fibers may be randomly arranged, flattened into a sheet called a chopped strand mat, or woven into glass c ...
. If classified by matrix then there are thermoplastic composites, short fibre thermoplastics, long fibre thermoplastics or long-fiber-reinforced thermoplastics. There are numerous thermoset
In materials science, a thermosetting polymer, often called a thermoset, is a polymer that is obtained by irreversibly hardening (" curing") a soft solid or viscous liquid prepolymer (resin). Curing is induced by heat or suitable radiation and ...
composites, including paper composite panels. Many advanced thermoset polymer matrix systems usually incorporate aramid fibre and carbon fibre
Carbon fiber-reinforced polymers (American English), carbon-fibre-reinforced polymers ( Commonwealth English), carbon-fiber-reinforced plastics, carbon-fiber reinforced-thermoplastic (CFRP, CRP, CFRTP), also known as carbon fiber, carbon comp ...
in an epoxy resin matrix.
Shape-memory polymer composites are high-performance composites, formulated using fibre or fabric reinforcements and shape-memory polymer resin as the matrix. Since a shape-memory polymer resin is used as the matrix, these composites have the ability to be easily manipulated into various configurations when they are heated above their activation temperatures and will exhibit high strength and stiffness at lower temperatures. They can also be reheated and reshaped repeatedly without losing their material properties. These composites are ideal for applications such as lightweight, rigid, deployable structures; rapid manufacturing; and dynamic reinforcement.
High strain composites are another type of high-performance composites that are designed to perform in a high deformation setting and are often used in deployable systems where structural flexing is advantageous. Although high strain composites exhibit many similarities to shape-memory polymers, their performance is generally dependent on the fibre layout as opposed to the resin content of the matrix.
Composites can also use metal fibres reinforcing other metals, as in metal matrix composite
In materials science, a metal matrix composite (MMC) is a composite material with fibers or particles dispersed in a metallic matrix, such as copper, aluminum, or steel. The secondary phase is typically a ceramic (such as alumina or silicon carb ...
s (MMC) or ceramic matrix composites (CMC), which includes bone
A bone is a rigid organ that constitutes part of the skeleton in most vertebrate animals. Bones protect the various other organs of the body, produce red and white blood cells, store minerals, provide structure and support for the body, ...
(hydroxyapatite
Hydroxyapatite (International Mineralogical Association, IMA name: hydroxylapatite) (Hap, HAp, or HA) is a naturally occurring mineral form of calcium apatite with the Chemical formula, formula , often written to denote that the Crystal struc ...
reinforced with collagen
Collagen () is the main structural protein in the extracellular matrix of the connective tissues of many animals. It is the most abundant protein in mammals, making up 25% to 35% of protein content. Amino acids are bound together to form a trip ...
fibres), cermet (ceramic and metal), and concrete
Concrete is a composite material composed of aggregate bound together with a fluid cement that cures to a solid over time. It is the second-most-used substance (after water), the most–widely used building material, and the most-manufactur ...
. Ceramic matrix composites are built primarily for fracture toughness
In materials science, fracture toughness is the critical stress intensity factor of a sharp Fracture, crack where propagation of the crack suddenly becomes rapid and unlimited. It is a material property that quantifies its ability to resist crac ...
, not for strength. Another class of composite materials involve woven fabric composite consisting of longitudinal and transverse laced yarns. Woven fabric composites are flexible as they are in form of fabric.
Organic matrix/ceramic aggregate composites include asphalt concrete
Asphalt concrete (commonly called asphalt, blacktop, or pavement in North America, and Tarmacadam, tarmac or bitumen macadam in the United Kingdom and the Republic of Ireland) is a composite material commonly used to surface road surface, roads ...
, polymer concrete, mastic asphalt, mastic roller hybrid, dental composite, syntactic foam, and mother of pearl. Chobham armour is a special type of composite armour
Composite armour is a type of vehicle armour consisting of layers of different materials such as metals, plastics, ceramics or air. Most composite armours are lighter than their all-metal equivalent, but instead occupy a larger volume for the sa ...
used in military applications.
Additionally, thermoplastic
A thermoplastic, or thermosoftening plastic, is any plastic polymer material that becomes pliable or moldable at a certain elevated temperature and solidifies upon cooling.
Most thermoplastics have a high molecular weight. The polymer chains as ...
composite materials can be formulated with specific metal powders resulting in materials with a density range from 2 g/cm3 to 11 g/cm3 (same density as lead). The most common name for this type of material is "high gravity compound" (HGC), although "lead replacement" is also used. These materials can be used in place of traditional materials such as aluminium, stainless steel, brass, bronze, copper, lead, and even tungsten in weighting, balancing (for example, modifying the centre of gravity of a tennis racquet
A racket or racquet is an item of sporting equipment used to strike a ball or shuttlecock in a variety of sports. A racket consists of three major components: a widened distal end known as the ''head'', an elongated handle known as the ''grip'' ...
), vibration damping, and radiation shielding applications. High density composites are an economically viable option when certain materials are deemed hazardous and are banned (such as lead) or when secondary operations costs (such as machining, finishing, or coating) are a factor.
There have been several studies indicating that interleaving stiff and brittle epoxy-based carbon-fiber-reinforced polymer
Carbon fiber-reinforced polymers (American English), carbon-fibre-reinforced polymers ( Commonwealth English), carbon-fiber-reinforced plastics, carbon-fiber reinforced-thermoplastic (CFRP, CRP, CFRTP), also known as carbon fiber, carbon comp ...
laminates with flexible thermoplastic laminates can help to make highly toughened composites that show improved impact resistance. Another interesting aspect of such interleaved composites is that they are able to have shape memory behaviour without needing any shape-memory polymers or shape-memory alloys e.g. balsa plies interleaved with hot glue, aluminium plies interleaved with acrylic polymers or PVC and carbon-fiber-reinforced polymer
Carbon fiber-reinforced polymers (American English), carbon-fibre-reinforced polymers ( Commonwealth English), carbon-fiber-reinforced plastics, carbon-fiber reinforced-thermoplastic (CFRP, CRP, CFRTP), also known as carbon fiber, carbon comp ...
laminates interleaved with polystyrene
Polystyrene (PS) is a synthetic polymer made from monomers of the aromatic hydrocarbon styrene. Polystyrene can be solid or foamed. General-purpose polystyrene is clear, hard, and brittle. It is an inexpensive resin per unit weight. It i ...
.
 A sandwich-structured composite is a special class of composite material that is fabricated by attaching two thin but stiff skins to a lightweight but thick core. The core material is normally low strength material, but its higher thickness provides the sandwich composite with high
A sandwich-structured composite is a special class of composite material that is fabricated by attaching two thin but stiff skins to a lightweight but thick core. The core material is normally low strength material, but its higher thickness provides the sandwich composite with high bending
In applied mechanics, bending (also known as flexure) characterizes the behavior of a slender structural element subjected to an external Structural load, load applied perpendicularly to a longitudinal axis of the element.
The structural eleme ...
stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force.
The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is.
Calculations
The stiffness, k, of a ...
with overall low density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
.
lignin
Lignin is a class of complex organic polymers that form key structural materials in the support tissues of most plants. Lignins are particularly important in the formation of cell walls, especially in wood and bark, because they lend rigidit ...
and hemicellulose
A hemicellulose (also known as polyose) is one of a number of heteropolymers (matrix polysaccharides), such as arabinoxylans, present along with cellulose in almost all embryophyte, terrestrial plant cell walls. Cellulose is crystalline, strong, an ...
matrix. Engineered wood
Engineered wood, also called mass timber, composite wood, man-made wood, or manufactured board, includes a range of derivative wood products which are manufactured by binding or fixing the strands, particles, fibres, veneers, or boards of wood, ...
includes a wide variety of different products such as wood fibre board, plywood, oriented strand board, wood plastic composite
Wood is a structural tissue/material found as xylem in the stems and roots of trees and other woody plants. It is an organic materiala natural composite of cellulosic fibers that are strong in tension and embedded in a matrix of lignin t ...
(recycled wood fibre in polyethylene matrix), Pykrete (sawdust in ice matrix), plastic-impregnated or laminated paper or textiles, Arborite, Formica (plastic), and Micarta. Other engineered laminate composites, such as Mallite, use a central core of end grain balsa wood, bonded to surface skins of light alloy
An alloy is a mixture of chemical elements of which in most cases at least one is a metal, metallic element, although it is also sometimes used for mixtures of elements; herein only metallic alloys are described. Metallic alloys often have prop ...
or GRP. These generate low-weight, high rigidity materials.
Particulate composites have particle as filler material dispersed in matrix, which may be nonmetal, such as glass, epoxy. Automobile tire is an example of particulate composite.
Advanced diamond-like carbon (DLC) coated polymer composites have been reported where the coating increases the surface hydrophobicity, hardness and wear resistance.
Ferromagnetic composites, including those with a polymer matrix consisting, for example, of nanocrystalline filler of Fe-based powders and polymers matrix. Amorphous and nanocrystalline powders obtained, for example, from metallic glasses can be used. Their use makes it possible to obtain ferromagnetic
Ferromagnetism is a property of certain materials (such as iron) that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromagne ...
nanocomposites with controlled magnetic properties.
Products
Fibre-reinforced composite materials have gained popularity (despite their generally high cost) in high-performance products that need to be lightweight, yet strong enough to take harsh loading conditions such asaerospace
Aerospace is a term used to collectively refer to the atmosphere and outer space. Aerospace activity is very diverse, with a multitude of commercial, industrial, and military applications. Aerospace engineering consists of aeronautics and astron ...
components (tail
The tail is the elongated section at the rear end of a bilaterian animal's body; in general, the term refers to a distinct, flexible appendage extending backwards from the midline of the torso. In vertebrate animals that evolution, evolved to los ...
s, wing
A wing is a type of fin that produces both Lift (force), lift and drag while moving through air. Wings are defined by two shape characteristics, an airfoil section and a planform (aeronautics), planform. Wing efficiency is expressed as lift-to-d ...
s, fuselage
The fuselage (; from the French language, French ''fuselé'' "spindle-shaped") is an aircraft's main body section. It holds Aircrew, crew, passengers, or cargo. In single-engine aircraft, it will usually contain an Aircraft engine, engine as wel ...
s, propeller
A propeller (often called a screw if on a ship or an airscrew if on an aircraft) is a device with a rotating hub and radiating blades that are set at a pitch to form a helical spiral which, when rotated, exerts linear thrust upon a working flu ...
s), boat and scull hulls, bicycle
A bicycle, also called a pedal cycle, bike, push-bike or cycle, is a human-powered transport, human-powered or motorized bicycle, motor-assisted, bicycle pedal, pedal-driven, single-track vehicle, with two bicycle wheel, wheels attached to a ...
frames, and racing car
Auto racing (also known as car racing, motor racing, or automobile racing) is a motorsport involving the racing of automobiles for competition. In North America, the term is commonly used to describe all forms of automobile sport including ...
bodies. Other uses include fishing rods, storage tanks, swimming pool panels, and baseball bats. The Boeing 787
The Boeing 787 Dreamliner is an American wide-body airliner developed and manufactured by Boeing Commercial Airplanes.
After dropping its unconventional Sonic Cruiser project, Boeing announced the conventional 7E7 on January 29, 2003, wh ...
and Airbus A350
The Airbus A350 is a flight length, long-range, wide-body twin-engine airliner developed and produced by Airbus.
The initial A350 design proposed in 2004, in response to the Boeing 787 Dreamliner, would have been a development of the Airbu ...
structures including the wings and fuselage are composed largely of composites. Composite materials are also becoming more common in the realm of orthopedic surgery, and it is the most common hockey stick material.
Carbon composite is a key material in today's launch vehicles and heat shields for the re-entry
Atmospheric entry (sometimes listed as Vimpact or Ventry) is the movement of an object from outer space into and through the gases of an atmosphere of a planet, dwarf planet, or natural satellite. Atmospheric entry may be ''uncontrolled entry ...
phase of spacecraft
A spacecraft is a vehicle that is designed spaceflight, to fly and operate in outer space. Spacecraft are used for a variety of purposes, including Telecommunications, communications, Earth observation satellite, Earth observation, Weather s ...
. It is widely used in solar panel substrates, antenna reflectors and yokes of spacecraft. It is also used in payload adapters, inter-stage structures and heat shields of launch vehicle
A launch vehicle is typically a rocket-powered vehicle designed to carry a payload (a crewed spacecraft or satellites) from Earth's surface or lower atmosphere to outer space. The most common form is the ballistic missile-shaped multistage ...
s. Furthermore, disk brake systems of airplane
An airplane (American English), or aeroplane (Commonwealth English), informally plane, is a fixed-wing aircraft that is propelled forward by thrust from a jet engine, Propeller (aircraft), propeller, or rocket engine. Airplanes come in a vari ...
s and racing cars are using carbon/carbon material, and the composite material
A composite or composite material (also composition material) is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a ...
with carbon fibre
Carbon fiber-reinforced polymers (American English), carbon-fibre-reinforced polymers ( Commonwealth English), carbon-fiber-reinforced plastics, carbon-fiber reinforced-thermoplastic (CFRP, CRP, CFRTP), also known as carbon fiber, carbon comp ...
s and silicon carbide
Silicon carbide (SiC), also known as carborundum (), is a hard chemical compound containing silicon and carbon. A wide bandgap semiconductor, it occurs in nature as the extremely rare mineral moissanite, but has been mass-produced as a powder a ...
matrix has been introduced in luxury vehicles and sports car
A sports car is a type of automobile that is designed with an emphasis on dynamic performance, such as Automobile handling, handling, acceleration, top speed, the thrill of driving, and Auto racing, racing capability. Sports cars originated in ...
s.
In 2006, a fibre-reinforced composite pool panel was introduced for in-ground swimming pools, residential as well as commercial, as a non-corrosive alternative to galvanized steel.
In 2007, an all-composite military Humvee
The High Mobility Multipurpose Wheeled Vehicle (HMMWV; colloquial: Humvee) is a family of Military light utility vehicle, light, four-wheel drive Military vehicle#Military trucks, military trucks and utility vehicles produced by AM General. It ...
was introduced by TPI Composites Inc and Armor Holdings Inc, the first all-composite military vehicle. By using composites the vehicle is lighter, allowing higher payloads. In 2008, carbon fibre and DuPont
Dupont, DuPont, Du Pont, duPont, or du Pont may refer to:
People
* Dupont (surname) Dupont, also spelled as DuPont, duPont, Du Pont, or du Pont is a French surname meaning "of the bridge", historically indicating that the holder of the surname re ...
Kevlar (five times stronger than steel) were combined with enhanced thermoset resins to make military transit cases by ECS Composites creating 30-percent lighter cases with high strength.
Pipes and fittings for various purpose like transportation of potable water, fire-fighting, irrigation, seawater, desalinated water, chemical and industrial waste, and sewage are now manufactured in glass reinforced plastics.
Composite materials used in tensile structures for facade application provides the advantage of being translucent. The woven base cloth combined with the appropriate coating allows better light transmission. This provides a very comfortable level of illumination compared to the full brightness of outside.
The wings of wind turbines, in growing sizes in the order of 50 m length are fabricated in composites since several years.
Two-lower-leg-amputees run on carbon-composite spring-like artificial feet as quick as non-amputee athletes.
High-pressure gas cylinders typically about 7–9 litre volume x 300 bar pressure for firemen are nowadays constructed from carbon composite. Type-4-cylinders include metal only as boss that carries the thread to screw in the valve.
On 5 September 2019, HMD Global unveiled the Nokia 6.2 and Nokia 7.2 which are claimed to be using polymer composite for the frames.
Overview
 Composite materials are created from individual materials. These individual materials are known as constituent materials, and there are two main categories of it. One is the
Composite materials are created from individual materials. These individual materials are known as constituent materials, and there are two main categories of it. One is the matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
( binder) and the other reinforcement
In Behaviorism, behavioral psychology, reinforcement refers to consequences that increase the likelihood of an organism's future behavior, typically in the presence of a particular ''Antecedent (behavioral psychology), antecedent stimulus''. Fo ...
. A portion of each kind is needed at least. The reinforcement receives support from the matrix as the matrix surrounds the reinforcement and maintains its relative positions. The properties of the matrix are improved as the reinforcements impart their exceptional physical and mechanical properties. The mechanical properties become unavailable from the individual constituent materials by synergism. At the same time, the designer of the product or structure receives options to choose an optimum combination from the variety of matrix and strengthening materials.
To shape the engineered composites, it must be formed. The reinforcement is placed onto the mould surface or into the mould cavity. Before or after this, the matrix can be introduced to the reinforcement. The matrix undergoes a melding event which sets the part shape necessarily. This melding event can happen in several ways, depending upon the matrix nature, such as solidification from the melted state for a thermoplastic polymer matrix composite or chemical polymerization
In polymer chemistry, polymerization (American English), or polymerisation (British English), is a process of reacting monomer molecules together in a chemical reaction to form polymer chains or three-dimensional networks. There are many fo ...
for a thermoset polymer matrix.
According to the requirements of end-item design, various methods of moulding can be used. The natures of the chosen matrix and reinforcement are the key factors influencing the methodology. The gross quantity of material to be made is another main factor. To support high capital investments for rapid and automated manufacturing technology, vast quantities can be used. Cheaper capital investments but higher labour and tooling expenses at a correspondingly slower rate assists the small production quantities.
Many commercially produced composites use a polymer
A polymer () is a chemical substance, substance or material that consists of very large molecules, or macromolecules, that are constituted by many repeat unit, repeating subunits derived from one or more species of monomers. Due to their br ...
matrix material often called a resin solution. There are many different polymers available depending upon the starting raw ingredients. There are several broad categories, each with numerous variations. The most common are known as polyester
Polyester is a category of polymers that contain one or two ester linkages in every repeat unit of their main chain. As a specific material, it most commonly refers to a type called polyethylene terephthalate (PET). Polyesters include some natura ...
, vinyl ester, epoxy
Epoxy is the family of basic components or Curing (chemistry), cured end products of epoxy Resin, resins. Epoxy resins, also known as polyepoxides, are a class of reactive prepolymers and polymers which contain epoxide groups. The epoxide fun ...
, phenolic, polyimide, polyamide
A polyamide is a polymer with repeating units linked by amide bonds.
Polyamides occur both naturally and artificially. Examples of naturally occurring polyamides are proteins, such as wool and silk. Artificially made polyamides can be made throug ...
, polypropylene
Polypropylene (PP), also known as polypropene, is a thermoplastic polymer used in a wide variety of applications. It is produced via chain-growth polymerization from the monomer Propene, propylene.
Polypropylene belongs to the group of polyolefin ...
, PEEK, and others. The reinforcement materials are often fibres but also commonly ground minerals. The various methods described below have been developed to reduce the resin content of the final product, or the fibre content is increased. As a rule of thumb, lay up results in a product containing 60% resin and 40% fibre, whereas vacuum infusion gives a final product with 40% resin and 60% fibre content. The strength of the product is greatly dependent on this ratio.
Martin Hubbe and Lucian A Lucia consider wood
Wood is a structural tissue/material found as xylem in the stems and roots of trees and other woody plants. It is an organic materiala natural composite of cellulosic fibers that are strong in tension and embedded in a matrix of lignin t ...
to be a natural composite of cellulose fibres in a matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
of lignin
Lignin is a class of complex organic polymers that form key structural materials in the support tissues of most plants. Lignins are particularly important in the formation of cell walls, especially in wood and bark, because they lend rigidit ...
.
Cores in composites
Several layup designs of composite also involve a co-curing or post-curing of the prepreg with many other media, such as foam or honeycomb. Generally, this is known as a sandwich structure. This is a more general layup for the production of cowlings, doors, radomes or non-structural parts. Open- and closed-cell-structuredfoam
Foams are two-phase materials science, material systems where a gas is dispersed in a second, non-gaseous material, specifically, in which gas cells are enclosed by a distinct liquid or solid material. Note, this source focuses only on liquid ...
s like polyvinyl chloride
Polyvinyl chloride (alternatively: poly(vinyl chloride), colloquial: vinyl or polyvinyl; abbreviated: PVC) is the world's third-most widely produced synthetic polymer of plastic (after polyethylene and polypropylene). About 40 million tons of ...
, polyurethane
Polyurethane (; often abbreviated PUR and PU) is a class of polymers composed of organic chemistry, organic units joined by carbamate (urethane) links. In contrast to other common polymers such as polyethylene and polystyrene, polyurethane term ...
, polyethylene
Polyethylene or polythene (abbreviated PE; IUPAC name polyethene or poly(methylene)) is the most commonly produced plastic. It is a polymer, primarily used for packaging (plastic bags, plastic films, geomembranes and containers including bott ...
, or polystyrene
Polystyrene (PS) is a synthetic polymer made from monomers of the aromatic hydrocarbon styrene. Polystyrene can be solid or foamed. General-purpose polystyrene is clear, hard, and brittle. It is an inexpensive resin per unit weight. It i ...
foams, balsa wood, syntactic foams, and honeycombs are generally utilized core materials. Open- and closed-cell metal foam can also be utilized as core materials. Recently, 3D graphene
Graphene () is a carbon allotrope consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice, honeycomb planar nanostructure. The name "graphene" is derived from "graphite" and the suffix -ene, indicating ...
structures ( also called graphene foam) have also been employed as core structures. A recent review by Khurram and Xu et al., have provided the summary of the state-of-the-art techniques for fabrication of the 3D structure of graphene, and the examples of the use of these foam like structures as a core for their respective polymer composites.
Semi-crystalline polymers
Although the two phases are chemically equivalent, semi-crystalline polymers can be described both quantitatively and qualitatively as composite materials. The crystalline portion has a higher elastic modulus and provides reinforcement for the less stiff, amorphous phase. Polymeric materials can range from 0% to 100% crystallinity aka volume fraction depending on molecular structure and thermal history. Different processing techniques can be employed to vary the percent crystallinity in these materials and thus the mechanical properties of these materials as described in the physical properties section. This effect is seen in a variety of places from industrial plastics like polyethylene shopping bags to spiders which can produce silks with different mechanical properties. In many cases these materials act like particle composites with randomly dispersed crystals known as spherulites. However they can also be engineered to be anisotropic and act more like fiber reinforced composites. In the case of spider silk, the properties of the material can even be dependent on the size of the crystals, independent of the volume fraction. Ironically, single component polymeric materials are some of the most easily tunable composite materials known.Methods of fabrication
Normally, the fabrication of composite includes wetting, mixing or saturating the reinforcement with the matrix. The matrix is then induced to bind together (with heat or a chemical reaction) into a rigid structure. Usually, the operation is done in an open or closed forming mould. However, the order and ways of introducing the constituents alters considerably. Composites fabrication is achieved by a wide variety of methods, including advanced fibre placement (automated fibre placement), fibreglass spray lay-up process, filament winding, lanxide process, tailored fibre placement, tufting, and z-pinning.Overview of mould
The reinforcing and matrix materials are merged, compacted, and cured (processed) within a mould to undergo a melding event. The part shape is fundamentally set after the melding event. However, under particular process conditions, it can deform. The melding event for a thermoset polymer matrix material is a curing reaction that is caused by the possibility of extra heat or chemical reactivity such as an organic peroxide. The melding event for a thermoplastic polymeric matrix material is a solidification from the melted state. The melding event for a metal matrix material such as titanium foil is a fusing at high pressure and a temperature near the melting point. It is suitable for many moulding methods to refer to one mould piece as a "lower" mould and another mould piece as an "upper" mould. Lower and upper does not refer to the mould's configuration in space, but the different faces of the moulded panel. There is always a lower mould, and sometimes an upper mould in this convention. Part construction commences by applying materials to the lower mould. Lower mould and upper mould are more generalized descriptors than more common and specific terms such as male side, female side, a-side, b-side, tool side, bowl, hat, mandrel, etc. Continuous manufacturing utilizes a different nomenclature. Usually, the moulded product is referred to as a panel. It can be referred to as casting for certain geometries and material combinations. It can be referred to as a profile for certain continuous processes. Some of the processes are autoclave moulding, vacuum bag moulding, pressure bag moulding, resin transfer moulding, and light resin transfer moulding.Other fabrication methods
Other types of fabrication includecasting
Casting is a manufacturing process in which a liquid material is usually poured into a mold, which contains a hollow cavity of the desired shape, and then allowed to solidify. The solidified part is also known as a casting, which is ejected or ...
, centrifugal casting, braiding (onto a former), continuous casting
Continuous casting, also called strand casting, is the process whereby melting, molten metal is solidified into a "semifinished" Billet (semi-finished product), billet, Bloom (casting)#Bloom, bloom, or Slab (casting)#Slab, slab for subsequent ro ...
, filament winding, press moulding, transfer moulding, pultrusion moulding, and slip forming
Slip forming, continuous poured, continuously formed, or slipform construction is a construction method in which concrete is placed into a form that may be in continuous motion horizontally, or incrementally raised vertically.
In horizontal c ...
. There are also forming capabilities including CNC filament winding, vacuum infusion, wet lay-up, compression moulding, and thermoplastic
A thermoplastic, or thermosoftening plastic, is any plastic polymer material that becomes pliable or moldable at a certain elevated temperature and solidifies upon cooling.
Most thermoplastics have a high molecular weight. The polymer chains as ...
moulding, to name a few. The practice of curing ovens and paint booths is also required for some projects.
Finishing methods
The composite parts finishing is also crucial in the final design. Many of these finishes will involve rain-erosion coatings or polyurethane coatings.Tooling
The mould and mould inserts are referred to as "tooling". The mould/tooling can be built from different materials. Tooling materials includealuminium
Aluminium (or aluminum in North American English) is a chemical element; it has chemical symbol, symbol Al and atomic number 13. It has a density lower than that of other common metals, about one-third that of steel. Aluminium has ...
, carbon fibre
Carbon fiber-reinforced polymers (American English), carbon-fibre-reinforced polymers ( Commonwealth English), carbon-fiber-reinforced plastics, carbon-fiber reinforced-thermoplastic (CFRP, CRP, CFRTP), also known as carbon fiber, carbon comp ...
, invar
Invar, also known generically as FeNi36 (64FeNi in the US), is a nickel–iron alloy notable for its uniquely low coefficient of thermal expansion (CTE or α). The name ''Invar'' comes from the word ''invariable'', referring to its relative lac ...
, nickel
Nickel is a chemical element; it has symbol Ni and atomic number 28. It is a silvery-white lustrous metal with a slight golden tinge. Nickel is a hard and ductile transition metal. Pure nickel is chemically reactive, but large pieces are slo ...
, reinforced silicone rubber and steel. The tooling material selection is normally based on, but not limited to, the coefficient of thermal expansion, expected number of cycles, end item tolerance, desired or expected surface condition, cure method, glass transition temperature
The glass–liquid transition, or glass transition, is the gradual and reversible transition in amorphous materials (or in amorphous regions within semicrystalline materials) from a hard and relatively brittle "glassy" state into a viscous or rub ...
of the material being moulded, moulding method, matrix, cost, and other various considerations.
Physical properties
anisotropic
Anisotropy () is the structural property of non-uniformity in different directions, as opposed to isotropy. An anisotropic object or pattern has properties that differ according to direction of measurement. For example, many materials exhibit ver ...
. This applies to many properties including elastic modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it.
Definition
The elastic modu ...
, ultimate tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate t ...
, thermal conductivity
The thermal conductivity of a material is a measure of its ability to heat conduction, conduct heat. It is commonly denoted by k, \lambda, or \kappa and is measured in W·m−1·K−1.
Heat transfer occurs at a lower rate in materials of low ...
, and electrical conductivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity in ...
. The ''rule of mixtures'' and ''inverse rule of mixtures'' give upper and lower bounds for these properties. The real value will lie somewhere between these values and can depend on many factors including:
* the orientation of interest
* the length of the fibres
* the accuracy of the fibre alignment
* the properties of the matrix and fibres
* delamination of the fibres and matrix
* the inclusion of any impurities
 For some material property , the rule of mixtures states that the overall property in the direction parallel to the fibers could be as high as
:
The inverse rule of mixtures states that in the direction
For some material property , the rule of mixtures states that the overall property in the direction parallel to the fibers could be as high as
:
The inverse rule of mixtures states that in the direction perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', � ...
to the fibers, the elastic modulus of a composite could be as low as
:
where
* is the volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
of the fibers
* is the material property of the composite parallel to the fibers
* is the material property of the composite perpendicular to the fibers
* is the material property of the fibers
* is the material property of the matrix
The majority of commercial composites are formed with random dispersion and orientation of the strengthening fibres, in which case the composite Young's modulus will fall between the isostrain and isostress bounds. However, in applications where the strength-to-weight ratio is engineered to be as high as possible (such as in the aerospace industry), fibre alignment may be tightly controlled.
In contrast to composites, isotropic materials (for example, aluminium or steel), in standard wrought forms, possess the same stiffness typically despite the directional orientation of the applied forces and/or moments. The relationship between forces/moments and strains/curvatures for an isotropic material can be described with the following material properties: Young's Modulus, the shear modulus
In materials science, shear modulus or modulus of rigidity, denoted by ''G'', or sometimes ''S'' or ''μ'', is a measure of the Elasticity (physics), elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear s ...
, and the Poisson's ratio, in relatively simple mathematical relationships. For the anisotropic material, it needs the mathematics of a second-order tensor and up to 21 material property constants. For the special case of orthogonal isotropy, there are three distinct material property constants for each of Young's Modulus, Shear Modulus and Poisson's ratio—a total of 9 constants to express the relationship between forces/moments and strains/curvatures.
Techniques that take benefit of the materials' anisotropic properties involve mortise and tenon joints (in natural composites such as wood) and pi joints in synthetic composites.
Mechanical properties of composites
Particle reinforcement
In general, particle reinforcement is strengthening the composites less thanfiber
Fiber (spelled fibre in British English; from ) is a natural or artificial substance that is significantly longer than it is wide. Fibers are often used in the manufacture of other materials. The strongest engineering materials often inco ...
reinforcement. It is used to enhance the stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force.
The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is.
Calculations
The stiffness, k, of a ...
of the composites while increasing the strength and the toughness
In materials science and metallurgy, toughness is the ability of a material to absorb energy and plastically deform without fracturing.mechanical properties, they are used in applications in which
 For fiber-reinforced composite, the fiber orientation in material affect anisotropic properties of the structure. From characterizing technique i.e. tensile testing, the material properties were measured based on sample (1-2) coordinate system. The tensors above express stress-strain relationship in (1-2) coordinate system. While the known material properties is in the principal coordinate system (x-y) of material. Transforming the tensor between two coordinate system help identify the material properties of the tested sample. The transformation matrix with degree rotation is
for for
For fiber-reinforced composite, the fiber orientation in material affect anisotropic properties of the structure. From characterizing technique i.e. tensile testing, the material properties were measured based on sample (1-2) coordinate system. The tensors above express stress-strain relationship in (1-2) coordinate system. While the known material properties is in the principal coordinate system (x-y) of material. Transforming the tensor between two coordinate system help identify the material properties of the tested sample. The transformation matrix with degree rotation is
for for
 Another failure mode is fiber tensile fracture, which becomes more likely when fibers are aligned with the loading direction, so is the possibility of fiber tensile fracture, assuming the tensile strength exceeds that of the matrix. When a fiber has some angle of misorientation θ, several fracture modes are possible. For small values of θ the stress required to initiate fracture is increased by a factor of (cos θ)−2 due to the increased cross-sectional area (''A'' cos θ) of the fibre and reduced force (''F/''cos θ) experienced by the fiber, leading to a composite tensile strength of ''σparallel /''cos2 θ where ''σparallel '' is the tensile strength of the composite with fibers aligned parallel with the applied force.
Intermediate angles of misorientation θ lead to matrix shear failure. Again the cross sectional area is modified but since
Another failure mode is fiber tensile fracture, which becomes more likely when fibers are aligned with the loading direction, so is the possibility of fiber tensile fracture, assuming the tensile strength exceeds that of the matrix. When a fiber has some angle of misorientation θ, several fracture modes are possible. For small values of θ the stress required to initiate fracture is increased by a factor of (cos θ)−2 due to the increased cross-sectional area (''A'' cos θ) of the fibre and reduced force (''F/''cos θ) experienced by the fiber, leading to a composite tensile strength of ''σparallel /''cos2 θ where ''σparallel '' is the tensile strength of the composite with fibers aligned parallel with the applied force.
Intermediate angles of misorientation θ lead to matrix shear failure. Again the cross sectional area is modified but since
cdmHUB – the Global Composites Community
Distance learning course in polymers and composites
OptiDAT composite material database
{{Authority control *
wear
Wear is the damaging, gradual removal or deformation of material at solid surfaces. Causes of wear can be mechanical (e.g., erosion) or chemical (e.g., corrosion). The study of wear and related processes is referred to as tribology.
Wear in ...
resistance is required. For example, hardness of cement
A cement is a binder, a chemical substance used for construction that sets, hardens, and adheres to other materials to bind them together. Cement is seldom used on its own, but rather to bind sand and gravel ( aggregate) together. Cement mi ...
can be increased by reinforcing gravel particles, drastically. Particle reinforcement a highly advantageous method of tuning mechanical properties of materials since it is very easy implement while being low cost.
The elastic modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it.
Definition
The elastic modu ...
of particle-reinforced composites can be expressed as,
:
where E is the elastic modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it.
Definition
The elastic modu ...
, V is the volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
. The subscripts c, p and m are indicating composite, particle and matrix, respectively. is a constant can be found empirically.
Similarly, tensile strength of particle-reinforced composites can be expressed as,
:
where T.S. is the tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
, and is a constant (not equal to ) that can be found empirically.
Short fiber reinforcement (shear lag theory)
Short fibers are often cheaper or more convenient to manufacture than longer continuous fibers, but still provide better properties than particle reinforcement. A common example is carbon fiber reinforced3D printing
3D printing, or additive manufacturing, is the construction of a three-dimensional object from a CAD model or a digital 3D model. It can be done in a variety of processes in which material is deposited, joined or solidified under computer ...
filaments, which use chopped short carbon fibers
Carbon fibers American and British English spelling differences, or carbon fibres (alternatively CF, graphite fiber or graphite fibre) are fibers about in diameter and composed mostly of carbon atoms. Carbon fibers have several advantages: ...
mixed into a matrix, typically PLA or PETG.
Shear lag theory uses the shear lag model to predict properties such as the Young's modulus for short fiber composites. The model assumes that load is transferred from the matrix to the fibers solely through the interfacial shear stresses acting on the cylindrical interface. Shear lag theory says then that the rate of change of the axial stress in the fiber as you move along the fiber is proportional to the ratio of the interfacial shear stresses over the radius of the fibre :
:
This leads to the average fiber stress over the full length of the fibre being given by:
:
where
* is the macroscopic strain in the composite
* is the ''fiber aspect ratio'' (length over diameter)
* is a dimensionless constant
* is the Poisson's ratio of the matrix
By assuming a uniform tensile strain, this results in:
:
As ''s'' becomes larger, this tends towards the rule of mixtures, which represents the Young's modulus parallel to continuous fibers.
Continuous fiber reinforcement
In general, continuousfiber
Fiber (spelled fibre in British English; from ) is a natural or artificial substance that is significantly longer than it is wide. Fibers are often used in the manufacture of other materials. The strongest engineering materials often inco ...
reinforcement is implemented by incorporating a fiber
Fiber (spelled fibre in British English; from ) is a natural or artificial substance that is significantly longer than it is wide. Fibers are often used in the manufacture of other materials. The strongest engineering materials often inco ...
as the strong phase into a weak phase, matrix. The reason for the popularity of fiber usage is materials with extraordinary strength can be obtained in their fiber form. Non-metallic fibers are usually showing a very high strength to density ratio compared to metal fibers because of the covalent
A covalent bond is a chemical bond that involves the sharing of electrons to form electron pairs between atoms. These electron pairs are known as shared pairs or bonding pairs. The stable balance of attractive and repulsive forces between atom ...
nature of their bonds. The most famous example of this is carbon fibers
Carbon fibers American and British English spelling differences, or carbon fibres (alternatively CF, graphite fiber or graphite fibre) are fibers about in diameter and composed mostly of carbon atoms. Carbon fibers have several advantages: ...
that have many applications extending from sports gear to protective equipment to space industries.
The stress on the composite can be expressed in terms of the volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
of the fiber and the matrix.
:
where is the stress, V is the volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
. The subscripts c, f and m are indicating composite, fiber and matrix, respectively.
Although the stress–strain behavior of fiber composites can only be determined by testing, there is an expected trend, three stages of the stress–strain curve. The first stage is the region of the stress–strain curve where both fiber and the matrix are elastically deformed. This linearly elastic region can be expressed in the following form.
:
where is the stress, is the strain, E is the elastic modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it.
Definition
The elastic modu ...
, and V is the volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
. The subscripts c, f, and m are indicating composite, fiber, and matrix, respectively.
After passing the elastic region for both fiber and the matrix, the second region of the stress–strain curve can be observed. In the second region, the fiber is still elastically deformed while the matrix is plastically deformed since the matrix is the weak phase. The instantaneous modulus can be determined using the slope of the stress–strain curve in the second region. The relationship between stress and strain can be expressed as,
:
where is the stress, is the strain, E is the elastic modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it.
Definition
The elastic modu ...
, and V is the volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
. The subscripts c, f, and m are indicating composite, fiber, and matrix, respectively. To find the modulus in the second region derivative of this equation can be used since the slope of the curve is equal to the modulus.
:
In most cases it can be assumed since the second term is much less than the first one.
In reality, the derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
of stress with respect to strain is not always returning the modulus because of the binding interaction between the fiber and matrix. The strength of the interaction between these two phases can result in changes in the mechanical properties of the composite. The compatibility of the fiber and matrix is a measure of internal stress.
The covalently bonded high strength fibers (e.g. carbon fibers
Carbon fibers American and British English spelling differences, or carbon fibres (alternatively CF, graphite fiber or graphite fibre) are fibers about in diameter and composed mostly of carbon atoms. Carbon fibers have several advantages: ...
) experience mostly elastic deformation before the fracture since the plastic deformation can happen due to dislocation motion. Whereas, metallic fibers have more space to plastically deform, so their composites exhibit a third stage where both fiber and the matrix are plastically deforming. Metallic fibers have many applications to work at cryogenic temperatures that is one of the advantages of composites with metal fibers over nonmetallic. The stress in this region of the stress–strain curve can be expressed as,
:
where is the stress, is the strain, E is the elastic modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it.
Definition
The elastic modu ...
, and V is the volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
. The subscripts c, f, and m are indicating composite, fiber, and matrix, respectively. and are for fiber and matrix flow stresses respectively. Just after the third region the composite exhibit necking. The necking strain of composite is happened to be between the necking strain of the fiber and the matrix just like other mechanical properties of the composites. The necking strain of the weak phase is delayed by the strong phase. The amount of the delay depends upon the volume fraction of the strong phase.
Thus, the tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
of the composite can be expressed in terms of the volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
.
:
where T.S. is the tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
, is the stress, is the strain, E is the elastic modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it.
Definition
The elastic modu ...
, and V is the volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
. The subscripts c, f, and m are indicating composite, fiber, and matrix, respectively. The composite tensile strength can be expressed as
: for is less than or equal to (arbitrary critical value of volume fraction)
: for is greater than or equal to
The critical value of volume fraction
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V'i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing:
:\varphi_i = \frac .
Being dimensionless quantit ...
can be expressed as,
:
Evidently, the composite tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
can be higher than the matrix if is greater than .
Thus, the minimum volume fraction of the fiber can be expressed as,
:
Although this minimum value is very low in practice, it is very important to know since the reason for the incorporation of continuous fibers is to improve the mechanical properties of the materials/composites, and this value of volume fraction is the threshold of this improvement.
The effect of fiber orientation
Aligned fibers
A change in the angle between the applied stress and fiber orientation will affect the mechanical properties of fiber-reinforced composites, especially the tensile strength. This angle, , can be used predict the dominant tensile fracture mechanism. At small angles, , the dominant fracture mechanism is the same as with load-fiber alignment, tensile fracture. The resolved force acting upon the length of the fibers is reduced by a factor of from rotation. . The resolved area on which the fiber experiences the force is increased by a factor of from rotation. . Taking the effectivetensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
to be and the aligned tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
.
:
At moderate angles, , the material experiences shear failure. The effective force direction is reduced with respect to the aligned direction. . The resolved area on which the force acts is . The resulting tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
depends on the shear strength of the matrix, .
:
At extreme angles, , the dominant mode of failure is tensile fracture in the matrix in the perpendicular direction. As in the isostress case of layered composite materials, the strength in this direction is lower than in the aligned direction. The effective areas and forces act perpendicular to the aligned direction so they both scale by . The resolved tensile strength is proportional to the transverse strength, .
:
The critical angles from which the dominant fracture mechanism changes can be calculated as,
:
:
where is the critical angle between longitudinal fracture and shear failure, and is the critical angle between shear failure and transverse fracture.
By ignoring length effects, this model is most accurate for continuous fibers and does not effectively capture the strength-orientation relationship for short fiber reinforced composites. Furthermore, most realistic systems do not experience the local maxima
In mathematical analysis, the maximum and minimum of a function (mathematics), function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given Interval (ma ...
predicted at the critical angles. The Tsai-Hill criterion provides a more complete description of fiber composite tensile strength as a function of orientation angle by coupling the contributing yield stresses: , , and .
:
Randomly oriented fibers
Anisotropy in the tensile strength of fiber reinforced composites can be removed by randomly orienting the fiber directions within the material. It sacrifices the ultimate strength in the aligned direction for an overall, isotropically strengthened material. : Where K is an empirically determined reinforcement factor; similar to the particle reinforcement equation. For fibers with randomly distributed orientations in a plane, , and for a random distribution in 3D, .Stiffness and Compliance Elasticity
Composite materials are generallyanisotropic
Anisotropy () is the structural property of non-uniformity in different directions, as opposed to isotropy. An anisotropic object or pattern has properties that differ according to direction of measurement. For example, many materials exhibit ver ...
, and in many cases are orthotropic. Voigt notation can be used to reduce the rank of the stress and strain tensors such that the stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force.
The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is.
Calculations
The stiffness, k, of a ...
(often also referred to by ) and compliance can be written as a matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
:
and
When considering each ply individually, it is assumed that they can be treated as thi lamina and so out–of–plane stresses and strains are negligible. That is and . This allows the stiffness and compliance matrices to be reduced to 3x3 matrices as follows:
and
 For fiber-reinforced composite, the fiber orientation in material affect anisotropic properties of the structure. From characterizing technique i.e. tensile testing, the material properties were measured based on sample (1-2) coordinate system. The tensors above express stress-strain relationship in (1-2) coordinate system. While the known material properties is in the principal coordinate system (x-y) of material. Transforming the tensor between two coordinate system help identify the material properties of the tested sample. The transformation matrix with degree rotation is
for for
For fiber-reinforced composite, the fiber orientation in material affect anisotropic properties of the structure. From characterizing technique i.e. tensile testing, the material properties were measured based on sample (1-2) coordinate system. The tensors above express stress-strain relationship in (1-2) coordinate system. While the known material properties is in the principal coordinate system (x-y) of material. Transforming the tensor between two coordinate system help identify the material properties of the tested sample. The transformation matrix with degree rotation is
for for
Types of fibers and mechanical properties
The most common types of fibers used in industry are glass fibers,carbon fibers
Carbon fibers American and British English spelling differences, or carbon fibres (alternatively CF, graphite fiber or graphite fibre) are fibers about in diameter and composed mostly of carbon atoms. Carbon fibers have several advantages: ...
, and kevlar
Kevlar (para-aramid) is a strong, heat-resistant synthetic fiber, related to other aramids such as Nomex and Technora. Developed by Stephanie Kwolek at DuPont in 1965, the high-strength material was first used commercially in the early 1970s as ...
due to their ease of production and availability. Their mechanical properties are very important to know, therefore the table of their mechanical properties is given below to compare them with S97 steel
Steel is an alloy of iron and carbon that demonstrates improved mechanical properties compared to the pure form of iron. Due to steel's high Young's modulus, elastic modulus, Yield (engineering), yield strength, Fracture, fracture strength a ...
. The angle of fiber orientation is very important because of the anisotropy of fiber composites (please see the section " Physical properties" for a more detailed explanation). The mechanical properties of the composites can be tested using standard mechanical testing methods by positioning the samples at various angles (the standard angles are 0°, 45°, and 90°) with respect to the orientation of fibers within the composites. In general, 0° axial alignment makes composites resistant to longitudinal bending and axial tension/compression, 90° hoop alignment is used to obtain resistance to internal/external pressure, and ± 45° is the ideal choice to obtain resistance against pure torsion.
Mechanical properties of fiber composite materials
Carbon fiber & fiberglass composites vs. aluminum alloy and steel
Although strength and stiffness ofsteel
Steel is an alloy of iron and carbon that demonstrates improved mechanical properties compared to the pure form of iron. Due to steel's high Young's modulus, elastic modulus, Yield (engineering), yield strength, Fracture, fracture strength a ...
and aluminum alloys are comparable to fiber composites, specific strength and stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force.
The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is.
Calculations
The stiffness, k, of a ...
of composites (i.e. in relation to their weight) are significantly higher.
Failure
Shock, impact of varying speed, or repeated cyclic stresses can provoke the laminate to separate at the interface between two layers, a condition known as delamination. Individual fibres can separate from the matrix, for example, fibre pull-out. Composites can fail on themacroscopic
The macroscopic scale is the length scale on which objects or phenomena are large enough to be visible with the naked eye, without magnifying optical instruments. It is the opposite of microscopic.
Overview
When applied to physical phenome ...
or microscopic
The microscopic scale () is the scale of objects and events smaller than those that can easily be seen by the naked eye, requiring a lens or microscope to see them clearly. In physics, the microscopic scale is sometimes regarded as the scale betwe ...
scale. Compression failures can happen at both the macro scale or at each individual reinforcing fibre in compression buckling. Tension failures can be net section failures of the part or degradation of the composite at a microscopic scale where one or more of the layers in the composite fail in tension of the matrix or failure of the bond between the matrix and fibres.
Some composites are brittle and possess little reserve strength beyond the initial onset of failure while others may have large deformations and have reserve energy absorbing capacity past the onset of damage. The distinctions in fibres and matrices that are available and the mixture
In chemistry, a mixture is a material made up of two or more different chemical substances which can be separated by physical method. It is an impure substance made up of 2 or more elements or compounds mechanically mixed together in any proporti ...
s that can be made with blends leave a very broad range of properties that can be designed into a composite structure. The most famous failure of a brittle ceramic matrix composite occurred when the carbon-carbon composite tile on the leading edge of the wing of the Space Shuttle Columbia
Space Shuttle ''Columbia'' (OV-102) was a Space Shuttle orbiter manufactured by Rockwell International and operated by NASA. Named after the Columbia Rediviva, first American ship to circumnavigate the globe, and the Columbia (personification) ...
fractured when impacted during take-off. It directed to the catastrophic break-up of the vehicle when it re-entered the Earth's atmosphere on 1 February 2003.
Composites have relatively poor bearing strength compared to metals.
 Another failure mode is fiber tensile fracture, which becomes more likely when fibers are aligned with the loading direction, so is the possibility of fiber tensile fracture, assuming the tensile strength exceeds that of the matrix. When a fiber has some angle of misorientation θ, several fracture modes are possible. For small values of θ the stress required to initiate fracture is increased by a factor of (cos θ)−2 due to the increased cross-sectional area (''A'' cos θ) of the fibre and reduced force (''F/''cos θ) experienced by the fiber, leading to a composite tensile strength of ''σparallel /''cos2 θ where ''σparallel '' is the tensile strength of the composite with fibers aligned parallel with the applied force.
Intermediate angles of misorientation θ lead to matrix shear failure. Again the cross sectional area is modified but since
Another failure mode is fiber tensile fracture, which becomes more likely when fibers are aligned with the loading direction, so is the possibility of fiber tensile fracture, assuming the tensile strength exceeds that of the matrix. When a fiber has some angle of misorientation θ, several fracture modes are possible. For small values of θ the stress required to initiate fracture is increased by a factor of (cos θ)−2 due to the increased cross-sectional area (''A'' cos θ) of the fibre and reduced force (''F/''cos θ) experienced by the fiber, leading to a composite tensile strength of ''σparallel /''cos2 θ where ''σparallel '' is the tensile strength of the composite with fibers aligned parallel with the applied force.
Intermediate angles of misorientation θ lead to matrix shear failure. Again the cross sectional area is modified but since shear stress
Shear stress (often denoted by , Greek alphabet, Greek: tau) is the component of stress (physics), stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross secti ...
is now the driving force for failure the area of the matrix parallel to the fibers is of interest, increasing by a factor of 1/sin θ. Similarly, the force parallel to this area again decreases (''F/''cos θ) leading to a total tensile strength of ''τmy /''sin θ cos θ where ''τmy'' is the matrix shear strength.
Finally, for large values of θ (near π/2) transverse matrix failure is the most likely to occur, since the fibers no longer carry the majority of the load. Still, the tensile strength will be greater than for the purely perpendicular orientation, since the force perpendicular to the fibers will decrease by a factor of 1/sin θ and the area decreases by a factor of 1/sin θ producing a composite tensile strength of ''σperp /''sin2θ where ''σperp '' is the tensile strength of the composite with fibers align perpendicular to the applied force.
Testing
Composites are tested before and after construction to assist in predicting and preventing failures. Pre-construction testing may adopt finite element analysis (FEA) for ply-by-ply analysis of curved surfaces and predicting wrinkling, crimping and dimpling of composites. Materials may be tested during manufacturing and after construction by various non-destructive methods including ultrasonic, thermography, shearography and X-ray radiography, and laser bond inspection for NDT of relative bond strength integrity in a localized area.See also
* 3D composites * Aluminium composite panel * American Composites Manufacturers Association * Chemical vapour infiltration * Composite laminate * Discontinuous aligned composite * Epoxy granite * Hybrid material * Lay-up process * Nanocomposite * Pykrete *Rule of mixtures
In materials science, a general rule of mixtures is a weighted mean used to predict various properties of a composite material . It provides a theoretical upper- and lower-bound on properties such as the elastic modulus, ultimate tensile strengt ...
* Scaled Composites
* Smart material
*'' Smart Materials and Structures''
* Void (composites)
References
Further reading
* * * * * * * * *External links
cdmHUB – the Global Composites Community
Distance learning course in polymers and composites
OptiDAT composite material database
{{Authority control *