extremal monomorphism on:
[Wikipedia]
[Google]
[Amazon]
In the context of
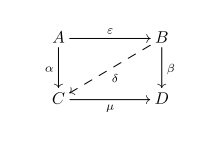 A monomorphism is said to be strong if for any epimorphism and any morphisms and such that , there exists a morphism such that and .
* A monomorphism is said to be split if there exists a morphism such that (in this case is called a left-sided inverse for ).
A monomorphism is said to be strong if for any epimorphism and any morphisms and such that , there exists a morphism such that and .
* A monomorphism is said to be split if there exists a morphism such that (in this case is called a left-sided inverse for ).
abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures. Algebraic structures include group (mathematics), groups, ring (mathematics), rings, field (mathematics), fields, module (mathe ...
or universal algebra
Universal algebra (sometimes called general algebra) is the field of mathematics that studies algebraic structures themselves, not examples ("models") of algebraic structures.
For instance, rather than take particular groups as the object of stu ...
, a monomorphism is an injective homomorphism
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type (such as two groups, two rings, or two vector spaces). The word ''homomorphism'' comes from the Ancient Greek language: () meaning "same" ...
. A monomorphism from to is often denoted with the notation .
In the more general setting of category theory, a monomorphism (also called a monic morphism or a mono) is a left-cancellative
In mathematics, the notion of cancellative is a generalization of the notion of invertible.
An element ''a'' in a magma has the left cancellation property (or is left-cancellative) if for all ''b'' and ''c'' in ''M'', always implies that .
A ...
morphism. That is, an arrow such that for all objects and all morphisms ,
:
Monomorphisms are a categorical generalization of injective functions (also called "one-to-one functions"); in some categories the notions coincide, but monomorphisms are more general, as in the examples below.
The categorical dual
In category theory, a branch of mathematics, duality is a correspondence between the properties of a category ''C'' and the dual properties of the opposite category ''C''op. Given a statement regarding the category ''C'', by interchanging the sou ...
of a monomorphism is an epimorphism
In category theory, an epimorphism (also called an epic morphism or, colloquially, an epi) is a morphism ''f'' : ''X'' → ''Y'' that is right-cancellative in the sense that, for all objects ''Z'' and all morphisms ,
: g_1 \circ f = g_2 \circ f ...
, that is, a monomorphism in a category ''C'' is an epimorphism in the dual category
In category theory, a branch of mathematics, the opposite category or dual category ''C''op of a given category ''C'' is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yield ...
''C''op. Every section
Section, Sectioning or Sectioned may refer to:
Arts, entertainment and media
* Section (music), a complete, but not independent, musical idea
* Section (typography), a subdivision, especially of a chapter, in books and documents
** Section sig ...
is a monomorphism, and every retraction is an epimorphism.
Relation to invertibility
Left-invertible morphisms are necessarily monic: if ''l'' is a left inverse for ''f'' (meaning ''l'' is a morphism and ), then ''f'' is monic, as : A left-invertible morphism is called a split mono or a section. However, a monomorphism need not be left-invertible. For example, in the category Group of allgroups
A group is a number of persons or things that are located, gathered, or classed together.
Groups of people
* Cultural group, a group whose members share the same cultural identity
* Ethnic group, a group whose members share the same ethnic ide ...
and group homomorphism
In mathematics, given two groups, (''G'', ∗) and (''H'', ·), a group homomorphism from (''G'', ∗) to (''H'', ·) is a function ''h'' : ''G'' → ''H'' such that for all ''u'' and ''v'' in ''G'' it holds that
: h(u*v) = h(u) \cdot h(v)
w ...
s among them, if ''H'' is a subgroup of ''G'' then the inclusion is always a monomorphism; but ''f'' has a left inverse in the category if and only if ''H'' has a normal complement in ''G''.
A morphism is monic if and only if the induced map , defined by for all morphisms , is injective for all objects ''Z''.
Examples
Every morphism in aconcrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets (or sometimes to another category, ''see Relative concreteness below''). This functor makes it possible to think of the objects of t ...
whose underlying function
Function or functionality may refer to:
Computing
* Function key, a type of key on computer keyboards
* Function model, a structured representation of processes in a system
* Function object or functor or functionoid, a concept of object-oriente ...
is injective is a monomorphism; in other words, if morphisms are actually functions between sets, then any morphism which is a one-to-one function will necessarily be a monomorphism in the categorical sense. In the category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets ''A'' and ''B'' are the total functions from ''A'' to ''B'', and the composition o ...
the converse also holds, so the monomorphisms are exactly the injective morphisms. The converse also holds in most naturally occurring categories of algebras because of the existence of a free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. Informally, a free object over a set ''A'' can be thought of as being a "generic" algebraic structure over ''A'': the only equations that hold between eleme ...
on one generator. In particular, it is true in the categories of all groups, of all ring
Ring may refer to:
* Ring (jewellery), a round band, usually made of metal, worn as ornamental jewelry
* To make a sound with a bell, and the sound made by a bell
:(hence) to initiate a telephone connection
Arts, entertainment and media Film and ...
s, and in any abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototypical example of an abelian category is the category of ...
.
It is not true in general, however, that all monomorphisms must be injective in other categories; that is, there are settings in which the morphisms are functions between sets, but one can have a function that is not injective and yet is a monomorphism in the categorical sense. For example, in the category Div of divisible
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by ...
(abelian) groups and group homomorphism
In mathematics, given two groups, (''G'', ∗) and (''H'', ·), a group homomorphism from (''G'', ∗) to (''H'', ·) is a function ''h'' : ''G'' → ''H'' such that for all ''u'' and ''v'' in ''G'' it holds that
: h(u*v) = h(u) \cdot h(v)
w ...
s between them there are monomorphisms that are not injective: consider, for example, the quotient map , where Q is the rationals under addition, Z the integers (also considered a group under addition), and Q/Z is the corresponding quotient group. This is not an injective map, as for example every integer is mapped to 0. Nevertheless, it is a monomorphism in this category. This follows from the implication , which we will now prove. If , where ''G'' is some divisible group, and , then . Now fix some . Without loss of generality, we may assume that (otherwise, choose −''x'' instead). Then, letting , since ''G'' is a divisible group, there exists some such that , so . From this, and , it follows that
:
Since , it follows that , and thus . This says that , as desired.
To go from that implication to the fact that ''q'' is a monomorphism, assume that for some morphisms , where ''G'' is some divisible group. Then , where . (Since , and , it follows that ). From the implication just proved, . Hence ''q'' is a monomorphism, as claimed.
Properties
*In atopos
In mathematics, a topos (, ; plural topoi or , or toposes) is a category that behaves like the category of sheaves of sets on a topological space (or more generally: on a site). Topoi behave much like the category of sets and possess a notio ...
, every mono is an equalizer, and any map that is both monic and epic is an isomorphism
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word i ...
.
*Every isomorphism is monic.
Related concepts
There are also useful concepts of ''regular monomorphism'', ''extremal monomorphism'', ''immediate monomorphism'', ''strong monomorphism'', and ''split monomorphism''. * A monomorphism is said to be regular if it is an equalizer of some pair of parallel morphisms. * A monomorphism is said to be extremal if in each representation , where is an epimorphism, the morphism is automatically anisomorphism
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word i ...
.
* A monomorphism is said to be immediate if in each representation , where is a monomorphism and is an epimorphism, the morphism is automatically an isomorphism
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word i ...
.
*  A monomorphism is said to be strong if for any epimorphism and any morphisms and such that , there exists a morphism such that and .
* A monomorphism is said to be split if there exists a morphism such that (in this case is called a left-sided inverse for ).
A monomorphism is said to be strong if for any epimorphism and any morphisms and such that , there exists a morphism such that and .
* A monomorphism is said to be split if there exists a morphism such that (in this case is called a left-sided inverse for ).
Terminology
The companion terms ''monomorphism'' and ''epimorphism'' were originally introduced by Nicolas Bourbaki; Bourbaki uses ''monomorphism'' as shorthand for an injective function. Early category theorists believed that the correct generalization of injectivity to the context of categories was the cancellation property given above. While this is not exactly true for monic maps, it is very close, so this has caused little trouble, unlike the case of epimorphisms.Saunders Mac Lane
Saunders Mac Lane (4 August 1909 – 14 April 2005) was an American mathematician who co-founded category theory with Samuel Eilenberg.
Early life and education
Mac Lane was born in Norwich, Connecticut, near where his family lived in Taftville ...
attempted to make a distinction between what he called ''monomorphisms'', which were maps in a concrete category whose underlying maps of sets were injective, and ''monic maps'', which are monomorphisms in the categorical sense of the word. This distinction never came into general use.
Another name for monomorphism is '' extension'', although this has other uses too.
See also
*Embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup.
When some object X is said to be embedded in another object Y, the embedding is g ...
* Nodal decomposition
* Subobject
Notes
References
* * * * *External links
* *{{nlab, id=strong+monomorphism, title=Strong monomorphism Morphisms Algebraic properties of elements