|
Nodal Decomposition
In category theory, an abstract mathematical discipline, a nodal decomposition of a morphism \varphi:X\to Y is a representation of \varphi as a product \varphi=\sigma\circ\beta\circ\pi, where \pi is a strong epimorphism, \beta a bimorphism, and \sigma a strong monomorphism.A monomorphism \mu:C\to D is said to be strong, if for any epimorphism \varepsilon:A\to B and for any morphisms \alpha:A\to C and \beta:B\to D such that \beta\circ\varepsilon=\mu\circ\alpha there exists a morphism \delta:B\to C, such that \delta\circ\varepsilon=\alpha and \mu\circ\delta=\beta Uniqueness and notations If it exists, the nodal decomposition is unique up to an isomorphism in the following sense: for any two nodal decompositions \varphi=\sigma\circ\beta\circ\pi and \varphi=\sigma'\circ\beta'\circ\pi' there exist isomorphisms \eta and \theta such that : \pi'=\eta\circ\pi, : \beta=\theta\circ\beta'\circ\eta, : \sigma'=\sigma\circ\theta. This property justifies some special notations for the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Additive Category
In mathematics, specifically in category theory, an additive category is a preadditive category C admitting all finitary biproducts. Definition A category C is preadditive if all its hom-sets are abelian groups and composition of morphisms is bilinear; in other words, C is enriched over the monoidal category of abelian groups. In a preadditive category, every finitary product (including the empty product, i.e., a final object) is necessarily a coproduct (or initial object in the case of an empty diagram), and hence a biproduct, and conversely every finitary coproduct is necessarily a product (this is a consequence of the definition, not a part of it). Thus an additive category is equivalently described as a preadditive category admitting all finitary products, or a preadditive category admitting all finitary coproducts. Another, yet equivalent, way to define an additive category is a category (not assumed to be preadditive) that has a zero object, finite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereotype Space
In the area of mathematics known as functional analysis, a reflexive space is a locally convex topological vector space (TVS) for which the canonical evaluation map from X into its bidual (which is the strong dual of the strong dual of X) is an isomorphism of TVSs. Since a normable TVS is reflexive if and only if it is semi-reflexive, every normed space (and so in particular, every Banach space) X is reflexive if and only if the canonical evaluation map from X into its bidual is surjective; in this case the normed space is necessarily also a Banach space. In 1951, R. C. James discovered a Banach space, now known as James' space, that is reflexive but is nevertheless isometrically isomorphic to its bidual (any such isomorphism is thus necessarily the canonical evaluation map). Reflexive spaces play an important role in the general theory of locally convex TVSs and in the theory of Banach spaces in particular. Hilbert spaces are prominent examples of reflexive Banach spaces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
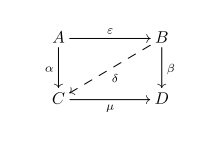
Strong Epimorphism
In category theory, an epimorphism (also called an epic morphism or, colloquially, an epi) is a morphism ''f'' : ''X'' → ''Y'' that is right-cancellative in the sense that, for all objects ''Z'' and all morphisms , : g_1 \circ f = g_2 \circ f \implies g_1 = g_2. Epimorphisms are categorical analogues of onto or surjective functions (and in the category of sets the concept corresponds exactly to the surjective functions), but they may not exactly coincide in all contexts; for example, the inclusion \mathbb\to\mathbb is a ring epimorphism. The dual of an epimorphism is a monomorphism (i.e. an epimorphism in a category ''C'' is a monomorphism in the dual category ''C''op). Many authors in abstract algebra and universal algebra define an epimorphism simply as an ''onto'' or surjective homomorphism. Every epimorphism in this algebraic sense is an epimorphism in the sense of category theory, but the converse is not true in all categories. In this article, the term "epimorphism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strong Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from to is often denoted with the notation X\hookrightarrow Y. In the more general setting of category theory, a monomorphism (also called a monic morphism or a mono) is a left-cancellative morphism. That is, an arrow such that for all objects and all morphisms , : f \circ g_1 = f \circ g_2 \implies g_1 = g_2. Monomorphisms are a categorical generalization of injective functions (also called "one-to-one functions"); in some categories the notions coincide, but monomorphisms are more general, as in the examples below. The categorical dual of a monomorphism is an epimorphism, that is, a monomorphism in a category ''C'' is an epimorphism in the dual category ''C''op. Every section is a monomorphism, and every retraction is an epimorphism. Relation to invertibility Left-invertible morphisms are necessarily monic: if ''l'' is a left inverse for ''f'' (meani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Limit
In mathematics, the inverse limit (also called the projective limit) is a construction that allows one to "glue together" several related objects, the precise gluing process being specified by morphisms between the objects. Thus, inverse limits can be defined in any category although their existence depends on the category that is considered. They are a special case of the concept of limit in category theory. By working in the dual category, that is by reverting the arrows, an inverse limit becomes a direct limit or ''inductive limit'', and a ''limit'' becomes a colimit. Formal definition Algebraic objects We start with the definition of an inverse system (or projective system) of groups and homomorphisms. Let (I, \leq) be a directed poset (not all authors require ''I'' to be directed). Let (''A''''i'')''i''∈''I'' be a family of groups and suppose we have a family of homomorphisms f_: A_j \to A_i for all i \leq j (note the order) with the following properties: # f_ is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Limit
In mathematics, a direct limit is a way to construct a (typically large) object from many (typically smaller) objects that are put together in a specific way. These objects may be groups, rings, vector spaces or in general objects from any category. The way they are put together is specified by a system of homomorphisms ( group homomorphism, ring homomorphism, or in general morphisms in the category) between those smaller objects. The direct limit of the objects A_i, where i ranges over some directed set I, is denoted by \varinjlim A_i . (This is a slight abuse of notation as it suppresses the system of homomorphisms that is crucial for the structure of the limit.) Direct limits are a special case of the concept of colimit in category theory. Direct limits are dual to inverse limits, which are also a special case of limits in category theory. Formal definition We will first give the definition for algebraic structures like groups and modules, and then the general defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelian Category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototypical example of an abelian category is the category of abelian groups, Ab. The theory originated in an effort to unify several cohomology theories by Alexander Grothendieck and independently in the slightly earlier work of David Buchsbaum. Abelian categories are very ''stable'' categories; for example they are regular and they satisfy the snake lemma. The class of abelian categories is closed under several categorical constructions, for example, the category of chain complexes of an abelian category, or the category of functors from a small category to an abelian category are abelian as well. These stability properties make them inevitable in homological algebra and beyond; the theory has major applications in algebraic geometry, cohomology and pure category theory. Abelian categories are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Refinement (category Theory)
In category theory and related fields of mathematics, a refinement is a construction that generalizes the operations of "interior enrichment", like bornologification or saturation of a locally convex space. A dual construction is called envelope. Definition Suppose K is a category, X an object in K, and \Gamma and \Phi two classes of morphisms in K. The definition of a refinement of X in the class \Gamma by means of the class \Phi consists of two steps. * A morphism \sigma:X'\to X in K is called an ''enrichment of the object X in the class of morphisms \Gamma by means of the class of morphisms \Phi'', if \sigma\in\Gamma, and for any morphism \varphi:B\to X from the class \Phi there exists a unique morphism \varphi':B\to X' in K such that \varphi=\sigma\circ\varphi'. * An enrichment \rho:E\to X of the object X in the class of morphisms \Gamma by means of the class of morphisms \Phi is called a ''refinement of X in \Gamma by means of \Phi'', if for any other enrichment \sigma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Envelope (category Theory)
In :Category theory and related fields of mathematics, an envelope is a construction that generalizes the operations of "exterior completion", like completion of a locally convex space, or Stone–Čech compactification of a topological space. A dual construction is called refinement. Definition Suppose K is a category, X an object in K, and \Omega and \Phi two classes of morphisms in K. The definition of an envelope of X in the class \Omega with respect to the class \Phi consists of two steps. * A morphism \sigma:X\to X' in K is called an ''extension of the object X in the class of morphisms \Omega with respect to the class of morphisms \Phi'', if \sigma\in\Omega, and for any morphism \varphi:X\to B from the class \Phi there exists a unique morphism \varphi':X'\to B in K such that \varphi=\varphi'\circ\sigma. * An extension \rho:X\to E of the object X in the class of morphisms \Omega with respect to the class of morphisms \Phi is called an ''envelope of X in \Omega with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pre-abelian Category
In mathematics, specifically in category theory, a pre-abelian category is an additive category that has all kernels and cokernels. Spelled out in more detail, this means that a category C is pre-abelian if: # C is preadditive, that is enriched over the monoidal category of abelian groups (equivalently, all hom-sets in C are abelian groups and composition of morphisms is bilinear); # C has all finite products (equivalently, all finite coproducts); note that because C is also preadditive, finite products are the same as finite coproducts, making them biproducts; # given any morphism ''f'': ''A'' → ''B'' in C, the equaliser of ''f'' and the zero morphism from ''A'' to ''B'' exists (this is by definition the kernel of ''f''), as does the coequaliser (this is by definition the cokernel of ''f''). Note that the zero morphism in item 3 can be identified as the identity element of the hom-set Hom(''A'',''B''), which is an abelian group by item 1; or as the unique ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |