Multivariate Adaptive Regression Splines on:
[Wikipedia]
[Google]
[Amazon]
In
 A
A  The figure on the right shows a plot of this function: the predicted versus ''x'', with the original values of ''y'' once again shown as red dots. The predicted response is now a better fit to the original ''y'' values.
MARS has automatically produced a kink in the predicted ''y'' to take into account non-linearity. The kink is produced by ''hinge functions''. The hinge functions are the expressions starting with (where is if , else ). Hinge functions are described in more detail below.
In this simple example, we can easily see from the plot that ''y'' has a non-linear relationship with ''x'' (and might perhaps guess that y varies with the square of ''x''). However, in general there will be multiple independent variables, and the relationship between ''y'' and these variables will be unclear and not easily visible by plotting. We can use MARS to discover that non-linear relationship.
An example MARS expression with multiple variables is
:
The figure on the right shows a plot of this function: the predicted versus ''x'', with the original values of ''y'' once again shown as red dots. The predicted response is now a better fit to the original ''y'' values.
MARS has automatically produced a kink in the predicted ''y'' to take into account non-linearity. The kink is produced by ''hinge functions''. The hinge functions are the expressions starting with (where is if , else ). Hinge functions are described in more detail below.
In this simple example, we can easily see from the plot that ''y'' has a non-linear relationship with ''x'' (and might perhaps guess that y varies with the square of ''x''). However, in general there will be multiple independent variables, and the relationship between ''y'' and these variables will be unclear and not easily visible by plotting. We can use MARS to discover that non-linear relationship.
An example MARS expression with multiple variables is
:
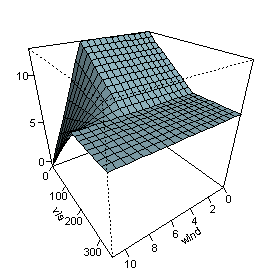 This expression models air pollution (the ozone level) as a function of the temperature and a few other variables. Note that the last term in the formula (on the last line) incorporates an interaction between and .
The figure on the right plots the predicted as and vary, with the other variables fixed at their median values. The figure shows that wind does not affect the ozone level unless visibility is low. We see that MARS can build quite flexible regression surfaces by combining hinge functions.
To obtain the above expression, the MARS model building procedure automatically selects which variables to use (some variables are important, others not), the positions of the kinks in the hinge functions, and how the hinge functions are combined.
This expression models air pollution (the ozone level) as a function of the temperature and a few other variables. Note that the last term in the formula (on the last line) incorporates an interaction between and .
The figure on the right plots the predicted as and vary, with the other variables fixed at their median values. The figure shows that wind does not affect the ozone level unless visibility is low. We see that MARS can build quite flexible regression surfaces by combining hinge functions.
To obtain the above expression, the MARS model building procedure automatically selects which variables to use (some variables are important, others not), the positions of the kinks in the hinge functions, and how the hinge functions are combined.
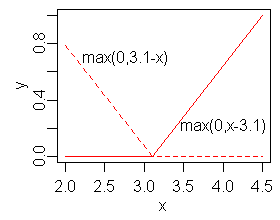 A key part of MARS models are ''hinge functions'' taking the form
:
or
:
where is a constant, called the ''knot''.
The figure on the right shows a mirrored pair of hinge functions with a knot at 3.1.
A hinge function is zero for part of its range, so can be used to partition the data into disjoint regions, each of which can be treated independently. Thus for example a mirrored pair of hinge functions in the expression
:
creates the
A key part of MARS models are ''hinge functions'' taking the form
:
or
:
where is a constant, called the ''knot''.
The figure on the right shows a mirrored pair of hinge functions with a knot at 3.1.
A hinge function is zero for part of its range, so can be used to partition the data into disjoint regions, each of which can be treated independently. Thus for example a mirrored pair of hinge functions in the expression
:
creates the
''The Elements of Statistical Learning''
2nd edition. Springer, (has a section on MARS) * Faraway J. (2005
''Extending the Linear Model with R''
CRC, (has an example using MARS with R) * Heping Zhang and Burton H. Singer (2010
''Recursive Partitioning and Applications''
2nd edition. Springer, (has a chapter on MARS and discusses some tweaks to the algorithm) * Denison D.G.T., Holmes C.C., Mallick B.K., and Smith A.F.M. (2004
Wiley, * Berk R.A. (2008) ''Statistical learning from a regression perspective'', Springer,
earth
/code> package **
/code> package **
/code> package. Not Friedman's MARS. **
/code> package for Bayesian MARS. * Matlab code: *
*
from the book ''Bayesian Methods for Nonlinear Classification and Regression''{{cite book , last1=Denison , first1=D. G. T. , last2=Holmes , first2=C. C. , last3=Mallick , first3=B. K. , last4=Smith , first4=A. F. M. , title=Bayesian methods for nonlinear classification and regression , date=2002 , publisher=Wiley , location=Chichester, England , isbn=978-0-471-49036-4 for Bayesian MARS. * Python *
Earth – Multivariate adaptive regression splines
*
py-earth
*
pyBASS
for Bayesian MARS. ; Commercial software:
MARS
from Salford Systems. Based on Friedman's implementation.
STATISTICA Data Miner
from StatSoft
from SAS. Nonparametric regression Machine learning
statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, multivariate adaptive regression splines (MARS) is a form of regression analysis introduced by Jerome H. Friedman in 1991. It is a non-parametric regression technique and can be seen as an extension of linear model
In statistics, the term linear model refers to any model which assumes linearity in the system. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However, t ...
s that automatically models nonlinearities and interactions between variables.
The term "MARS" is trademarked and licensed to Salford Systems. In order to avoid trademark infringements, many open-source implementations of MARS are called "Earth".
The basics
This section introduces MARS using a few examples. We start with a set of data: a matrix of input variables ''x'', and a vector of the observed responses ''y'', with a response for each row in ''x''. For example, the data could be: Here there is only one independent variable, so the ''x'' matrix is just a single column. Given these measurements, we would like to build a model which predicts the expected ''y'' for a given ''x''. A
A linear model
In statistics, the term linear model refers to any model which assumes linearity in the system. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However, t ...
for the above data is
:
The hat on the indicates that is estimated from the data. The figure on the right shows a plot of this function:
a line giving the predicted versus ''x'', with the original values of ''y'' shown as red dots.
The data at the extremes of ''x'' indicates that the relationship between ''y'' and ''x'' may be non-linear (look at the red dots relative to the regression line at low and high values of ''x''). We thus turn to MARS to automatically build a model taking into account non-linearities. MARS software constructs a model from the given ''x'' and ''y'' as follows
:
 The figure on the right shows a plot of this function: the predicted versus ''x'', with the original values of ''y'' once again shown as red dots. The predicted response is now a better fit to the original ''y'' values.
MARS has automatically produced a kink in the predicted ''y'' to take into account non-linearity. The kink is produced by ''hinge functions''. The hinge functions are the expressions starting with (where is if , else ). Hinge functions are described in more detail below.
In this simple example, we can easily see from the plot that ''y'' has a non-linear relationship with ''x'' (and might perhaps guess that y varies with the square of ''x''). However, in general there will be multiple independent variables, and the relationship between ''y'' and these variables will be unclear and not easily visible by plotting. We can use MARS to discover that non-linear relationship.
An example MARS expression with multiple variables is
:
The figure on the right shows a plot of this function: the predicted versus ''x'', with the original values of ''y'' once again shown as red dots. The predicted response is now a better fit to the original ''y'' values.
MARS has automatically produced a kink in the predicted ''y'' to take into account non-linearity. The kink is produced by ''hinge functions''. The hinge functions are the expressions starting with (where is if , else ). Hinge functions are described in more detail below.
In this simple example, we can easily see from the plot that ''y'' has a non-linear relationship with ''x'' (and might perhaps guess that y varies with the square of ''x''). However, in general there will be multiple independent variables, and the relationship between ''y'' and these variables will be unclear and not easily visible by plotting. We can use MARS to discover that non-linear relationship.
An example MARS expression with multiple variables is
:
 This expression models air pollution (the ozone level) as a function of the temperature and a few other variables. Note that the last term in the formula (on the last line) incorporates an interaction between and .
The figure on the right plots the predicted as and vary, with the other variables fixed at their median values. The figure shows that wind does not affect the ozone level unless visibility is low. We see that MARS can build quite flexible regression surfaces by combining hinge functions.
To obtain the above expression, the MARS model building procedure automatically selects which variables to use (some variables are important, others not), the positions of the kinks in the hinge functions, and how the hinge functions are combined.
This expression models air pollution (the ozone level) as a function of the temperature and a few other variables. Note that the last term in the formula (on the last line) incorporates an interaction between and .
The figure on the right plots the predicted as and vary, with the other variables fixed at their median values. The figure shows that wind does not affect the ozone level unless visibility is low. We see that MARS can build quite flexible regression surfaces by combining hinge functions.
To obtain the above expression, the MARS model building procedure automatically selects which variables to use (some variables are important, others not), the positions of the kinks in the hinge functions, and how the hinge functions are combined.
The MARS model
MARS builds models of the form : The model is a weighted sum of basis functions . Each is a constant coefficient. For example, each line in the formula for ozone above is one basis function multiplied by its coefficient. Each basis function takes one of the following three forms: 1) a constant 1. There is just one such term, the intercept. In the ozone formula above, the intercept term is 5.2. 2) a ''hinge'' function. A hinge function has the form or . MARS automatically selects variables and values of those variables for knots of the hinge functions. Examples of such basis functions can be seen in the middle three lines of the ozone formula. 3) a product of two or more hinge functions. These basis functions can model interaction between two or more variables. An example is the last line of the ozone formula.Hinge functions
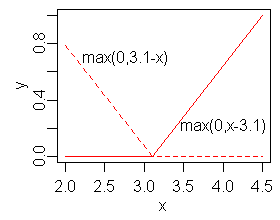 A key part of MARS models are ''hinge functions'' taking the form
:
or
:
where is a constant, called the ''knot''.
The figure on the right shows a mirrored pair of hinge functions with a knot at 3.1.
A hinge function is zero for part of its range, so can be used to partition the data into disjoint regions, each of which can be treated independently. Thus for example a mirrored pair of hinge functions in the expression
:
creates the
A key part of MARS models are ''hinge functions'' taking the form
:
or
:
where is a constant, called the ''knot''.
The figure on the right shows a mirrored pair of hinge functions with a knot at 3.1.
A hinge function is zero for part of its range, so can be used to partition the data into disjoint regions, each of which can be treated independently. Thus for example a mirrored pair of hinge functions in the expression
:
creates the piecewise
In mathematics, a piecewise function (also called a piecewise-defined function, a hybrid function, or a function defined by cases) is a function whose domain is partitioned into several intervals ("subdomains") on which the function may be ...
linear graph shown for the simple MARS model in the previous section.
One might assume that only piecewise linear functions can be formed from hinge functions, but hinge functions can be multiplied together to form non-linear functions.
Hinge functions are also called ramp, hockey stick, or rectifier
A rectifier is an electrical device that converts alternating current (AC), which periodically reverses direction, to direct current (DC), which flows in only one direction.
The process is known as ''rectification'', since it "straightens" t ...
functions. Instead of the notation used in this article, hinge functions are often represented by where means take the positive part.
The model building process
MARS builds a model in two phases: the forward and the backward pass. This two-stage approach is the same as that used byrecursive partitioning
Recursive partitioning is a statistics, statistical method for multivariable analysis. Recursive partitioning creates a Decision tree learning, decision tree that strives to correctly classify members of the population by splitting it into sub-popu ...
trees.
The forward pass
MARS starts with a model which consists of just the intercept term (which is the mean of the response values). MARS then repeatedly adds basis function in pairs to the model. At each step it finds the pair of basis functions that gives the maximum reduction in sum-of-squares residual error (it is a greedy algorithm). The two basis functions in the pair are identical except that a different side of a mirrored hinge function is used for each function. Each new basis function consists of a term already in the model (which could perhaps be the intercept term) multiplied by a new hinge function. A hinge function is defined by a variable and a knot, so to add a new basis function, MARS must search over all combinations of the following: 1) existing terms (called ''parent terms'' in this context) 2) all variables (to select one for the new basis function) 3) all values of each variable (for the knot of the new hinge function). To calculate the coefficient of each term, MARS applies a linear regression over the terms. This process of adding terms continues until the change in residual error is too small to continue or until the maximum number of terms is reached. The maximum number of terms is specified by the user before model building starts. The search at each step is usually done in a brute-force fashion, but a key aspect of MARS is that because of the nature of hinge functions, the search can be done quickly using a fast least-squares update technique. Brute-force search can be sped up by using aheuristic
A heuristic or heuristic technique (''problem solving'', '' mental shortcut'', ''rule of thumb'') is any approach to problem solving that employs a pragmatic method that is not fully optimized, perfected, or rationalized, but is nevertheless ...
that reduces the number of parent terms considered at each step ("Fast MARS").
The backward pass
The forward pass usually overfits the model. To build a model with better generalization ability, the backward pass prunes the model, deleting the least effective term at each step until it finds the best submodel. Model subsets are compared using the Generalized cross validation (GCV) criterion described below. The backward pass has an advantage over the forward pass: at any step it can choose any term to delete, whereas the forward pass at each step can only see the next pair of terms. The forward pass adds terms in pairs, but the backward pass typically discards one side of the pair and so terms are often not seen in pairs in the final model. A paired hinge can be seen in the equation for in the first MARS example above; there are no complete pairs retained in the ozone example.Generalized cross validation
The backward pass compares the performance of different models using Generalized Cross-Validation (GCV), a minor variant on the Akaike information criterion that approximates the leave-one-out cross-validation score in the special case where errors are Gaussian, or where the squared error loss function is used. GCV was introduced by Craven and Wahba and extended by Friedman for MARS; lower values of GCV indicate better models. The formula for the GCV is : GCV = RSS / (''N'' · (1 − (effective number of parameters) / ''N'')2) where RSS is the residual sum-of-squares measured on the training data and ''N'' is the number of observations (the number of rows in the x matrix). The effective number of parameters is defined as : (effective number of parameters) = (number of mars terms) + (penalty) · ((number of Mars terms) − 1 ) / 2 where penalty is typically 2 (giving results equivalent to the Akaike information criterion) but can be increased by the user if they so desire. Note that : (number of Mars terms − 1 ) / 2 is the number of hinge-function knots, so the formula penalizes the addition of knots. Thus the GCV formula adjusts (i.e. increases) the training RSS to penalize more complex models. We penalize flexibility because models that are too flexible will model the specific realization of noise in the data instead of just the systematic structure of the data.Constraints
One constraint has already been mentioned: the user can specify the maximum number of terms in the forward pass. A further constraint can be placed on the forward pass by specifying a maximum allowable degree of interaction. Typically only one or two degrees of interaction are allowed, but higher degrees can be used when the data warrants it. The maximum degree of interaction in the first MARS example above is one (i.e. no interactions or an ''additive model''); in the ozone example it is two. Other constraints on the forward pass are possible. For example, the user can specify that interactions are allowed only for certain input variables. Such constraints could make sense because of knowledge of the process that generated the data.Pros and cons
No regression modeling technique is best for all situations. The guidelines below are intended to give an idea of the pros and cons of MARS, but there will be exceptions to the guidelines. It is useful to compare MARS torecursive partitioning
Recursive partitioning is a statistics, statistical method for multivariable analysis. Recursive partitioning creates a Decision tree learning, decision tree that strives to correctly classify members of the population by splitting it into sub-popu ...
and this is done below.
(Recursive partitioning is also commonly called ''regression trees'',
''decision trees'', or CART;
see the recursive partitioning
Recursive partitioning is a statistics, statistical method for multivariable analysis. Recursive partitioning creates a Decision tree learning, decision tree that strives to correctly classify members of the population by splitting it into sub-popu ...
article for details).
*MARS models are more flexible than linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ...
models.
*MARS models are simple to understand and interpret. Compare the equation for ozone concentration above to, say, the innards of a trained neural network
A neural network is a group of interconnected units called neurons that send signals to one another. Neurons can be either biological cells or signal pathways. While individual neurons are simple, many of them together in a network can perfor ...
or a random forest.
*MARS can handle both continuous and categorical data. MARS tends to be better than recursive partitioning for numeric data because hinges are more appropriate for numeric variables than the piecewise constant segmentation used by recursive partitioning.
*Building MARS models often requires little or no data preparation. The hinge functions automatically partition the input data, so the effect of outliers is contained. In this respect MARS is similar to recursive partitioning
Recursive partitioning is a statistics, statistical method for multivariable analysis. Recursive partitioning creates a Decision tree learning, decision tree that strives to correctly classify members of the population by splitting it into sub-popu ...
which also partitions the data into disjoint regions, although using a different method.
*MARS (like recursive partitioning) does automatic variable selection (meaning it includes important variables in the model and excludes unimportant ones). However, there can be some arbitrariness in the selection, especially when there are correlated predictors, and this can affect interpretability.
*MARS models tend to have a good bias-variance trade-off. The models are flexible enough to model non-linearity and variable interactions (thus MARS models have fairly low bias), yet the constrained form of MARS basis functions prevents too much flexibility (thus MARS models have fairly low variance).
*MARS is suitable for handling large datasets, and implementations run very quickly. However, recursive partitioning can be faster than MARS.
*With MARS models, as with any non-parametric regression, parameter confidence intervals and other checks on the model cannot be calculated directly (unlike linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ...
models). Cross-validation and related techniques must be used for validating the model instead.
*The earth, mda, and polspline implementations do not allow missing values in predictors, but free implementations of regression trees (such as rpart and party) do allow missing values using a technique called surrogate splits.
*MARS models can make predictions very quickly, as they only require evaluating a linear function of the predictors.
*The resulting fitted function is continuous, unlike recursive partitioning, which can give a more realistic model in some situations. (However, the model is not smooth or differentiable).
Extensions and related concepts
*Generalized linear model
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by ...
s (GLMs) can be incorporated into MARS models by applying a link function after the MARS model is built. Thus, for example, MARS models can incorporate logistic regression
In statistics, a logistic model (or logit model) is a statistical model that models the logit, log-odds of an event as a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regres ...
to predict probabilities.
* Non-linear regression is used when the underlying form of the function is known and regression is used only to estimate the parameters of that function. MARS, on the other hand, estimates the functions themselves, albeit with severe constraints on the nature of the functions. (These constraints are necessary because discovering a model from the data is an inverse problem
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, sound source reconstruction, source reconstruction in ac ...
that is not well-posed without constraints on the model.)
* Recursive partitioning
Recursive partitioning is a statistics, statistical method for multivariable analysis. Recursive partitioning creates a Decision tree learning, decision tree that strives to correctly classify members of the population by splitting it into sub-popu ...
(commonly called CART). MARS can be seen as a generalization of recursive partitioning that allows for continuous models, which can provide a better fit for numerical data.
* Generalized additive models. Unlike MARS, GAMs fit smooth loess
A loess (, ; from ) is a clastic rock, clastic, predominantly silt-sized sediment that is formed by the accumulation of wind-blown dust. Ten percent of Earth's land area is covered by loesses or similar deposition (geology), deposits.
A loess ...
or polynomial splines rather than hinge functions, and they do not automatically model variable interactions. The smoother fit and lack of regression terms reduces variance when compared to MARS, but ignoring variable interactions can worsen the bias.
* TSMARS. Time Series Mars is the term used when MARS models are applied in a time series context. Typically in this set up the predictors are the lagged time series values resulting in autoregressive spline models. These models and extensions to include moving average spline models are described in "Univariate Time Series Modelling and Forecasting using TSMARS: A study of threshold time series autoregressive, seasonal and moving average models using TSMARS".
* Bayesian MARS (BMARS) uses the same model form, but builds the model using a Bayesian approach. It may arrive at different optimal MARS models because the model building approach is different. The result of BMARS is typically an ensemble of posterior samples of MARS models, which allows for probabilistic prediction.
See also
*Linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ...
* Local regression
* Rational function modeling
* Segmented regression
* Spline interpolation
* Spline regression
References
Further reading
* Hastie T., Tibshirani R., and Friedman J.H. (2009''The Elements of Statistical Learning''
2nd edition. Springer, (has a section on MARS) * Faraway J. (2005
''Extending the Linear Model with R''
CRC, (has an example using MARS with R) * Heping Zhang and Burton H. Singer (2010
''Recursive Partitioning and Applications''
2nd edition. Springer, (has a chapter on MARS and discusses some tweaks to the algorithm) * Denison D.G.T., Holmes C.C., Mallick B.K., and Smith A.F.M. (2004
Wiley, * Berk R.A. (2008) ''Statistical learning from a regression perspective'', Springer,
External links
Several free and commercial software packages are available for fitting MARS-type models. ; Free software: * R packages: **earth function in the /code> package **
mars function in the /code> package **
polymars function in the /code> package. Not Friedman's MARS. **
bass function in the /code> package for Bayesian MARS. * Matlab code: *
*
from the book ''Bayesian Methods for Nonlinear Classification and Regression''{{cite book , last1=Denison , first1=D. G. T. , last2=Holmes , first2=C. C. , last3=Mallick , first3=B. K. , last4=Smith , first4=A. F. M. , title=Bayesian methods for nonlinear classification and regression , date=2002 , publisher=Wiley , location=Chichester, England , isbn=978-0-471-49036-4 for Bayesian MARS. * Python *
Earth – Multivariate adaptive regression splines
*
py-earth
*
pyBASS
for Bayesian MARS. ; Commercial software:
MARS
from Salford Systems. Based on Friedman's implementation.
STATISTICA Data Miner
from StatSoft
from SAS. Nonparametric regression Machine learning