Gaussian Function on:
[Wikipedia]
[Google]
[Amazon]
In
 Base form:
In two dimensions, the power to which ''e'' is raised in the Gaussian function is any negative-definite quadratic form. Consequently, the level sets of the Gaussian will always be ellipses.
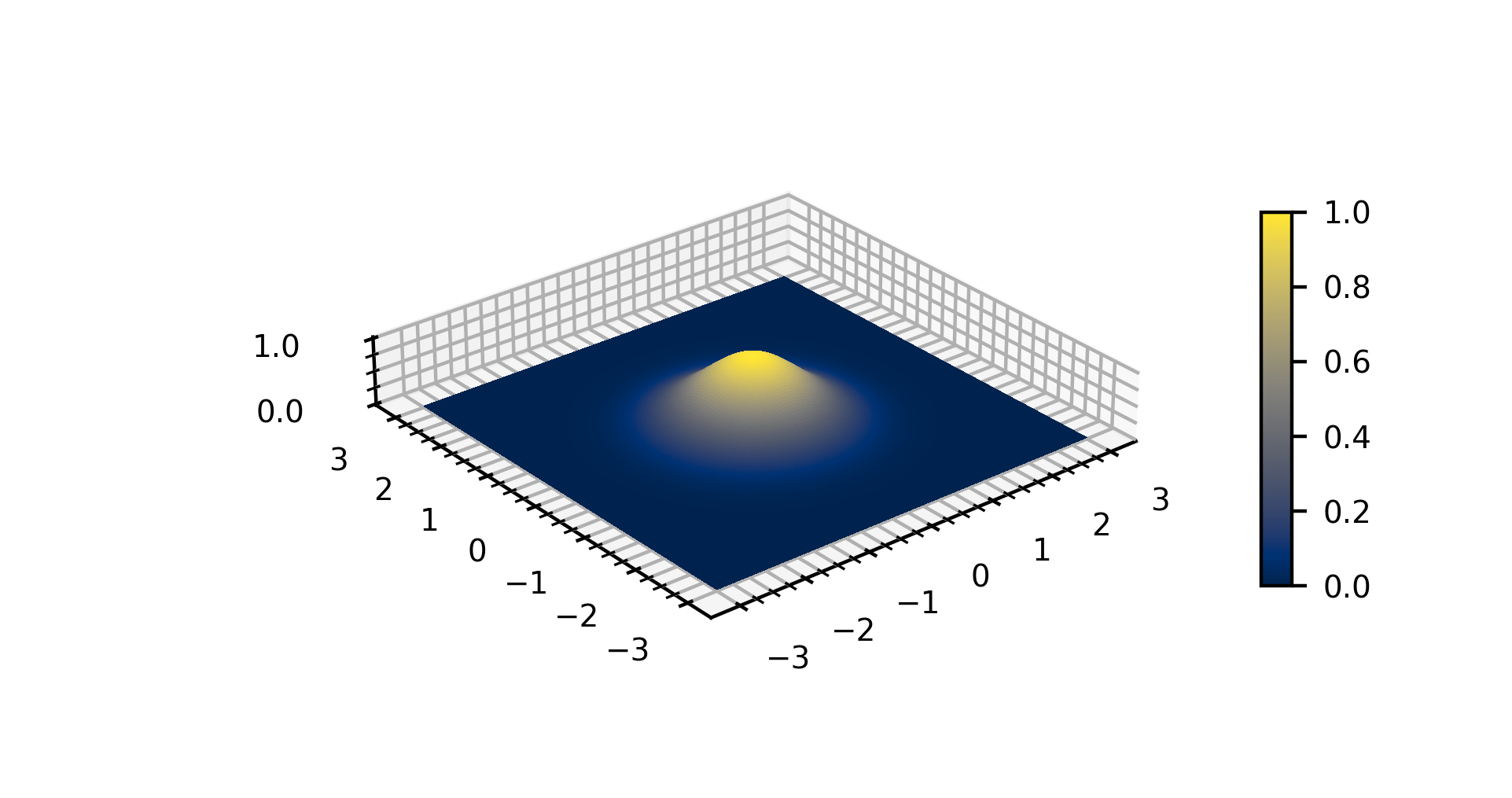
A particular example of a two-dimensional Gaussian function is
Here the coefficient ''A'' is the amplitude, ''x''0, ''y''0 is the center, and ''σ''''x'', ''σ''''y'' are the ''x'' and ''y'' spreads of the blob. The figure on the right was created using ''A'' = 1, ''x''0 = 0, ''y''0 = 0, ''σ''''x'' = ''σ''''y'' = 1.
The volume under the Gaussian function is given by
In general, a two-dimensional elliptical Gaussian function is expressed as
where the matrix
is positive-definite.
Using this formulation, the figure on the right can be created using , , , .
Base form:
In two dimensions, the power to which ''e'' is raised in the Gaussian function is any negative-definite quadratic form. Consequently, the level sets of the Gaussian will always be ellipses.
A particular example of a two-dimensional Gaussian function is
Here the coefficient ''A'' is the amplitude, ''x''0, ''y''0 is the center, and ''σ''''x'', ''σ''''y'' are the ''x'' and ''y'' spreads of the blob. The figure on the right was created using ''A'' = 1, ''x''0 = 0, ''y''0 = 0, ''σ''''x'' = ''σ''''y'' = 1.
The volume under the Gaussian function is given by
In general, a two-dimensional elliptical Gaussian function is expressed as
where the matrix
is positive-definite.
Using this formulation, the figure on the right can be created using , , , .
A = 1;
x0 = 0; y0 = 0;
sigma_X = 1;
sigma_Y = 2;
, Y= meshgrid(-5:.1:5, -5:.1:5);
for theta = 0:pi/100:pi
a = cos(theta)^2 / (2 * sigma_X^2) + sin(theta)^2 / (2 * sigma_Y^2);
b = sin(2 * theta) / (4 * sigma_X^2) - sin(2 * theta) / (4 * sigma_Y^2);
c = sin(theta)^2 / (2 * sigma_X^2) + cos(theta)^2 / (2 * sigma_Y^2);
Z = A * exp(-(a * (X - x0).^2 + 2 * b * (X - x0) .* (Y - y0) + c * (Y - y0).^2));
surf(X, Y, Z);
shading interp;
view(-36, 36)
waitforbuttonpress
end
Such functions are often used in
/ref> While this provides a simple curve fitting procedure, the resulting algorithm may be biased by excessively weighting small data values, which can produce large errors in the profile estimate. One can partially compensate for this problem through
/ref>N. Hagen and E. L. Dereniak, "Gaussian profile estimation in two dimensions," Appl. Opt. 47:6842–6851 (2008)
/ref> # The noise in the measured profile is either i.i.d. Gaussian, or the noise is
 One may ask for a discrete analog to the Gaussian;
this is necessary in discrete applications, particularly
One may ask for a discrete analog to the Gaussian;
this is necessary in discrete applications, particularly
/ref> where denotes the
Stochastic Simulation of Patterns Using Distance-Based Pattern Modeling
', Mathematical Geosciences, 42: 487–517
Mathworld, includes a proof for the relations between c and FWHM
* {{MathPages, id=home/kmath045/kmath045, title=Integrating The Bell Curve
Haskell, Erlang and Perl implementation of Gaussian distribution
Bensimhoun Michael, ''N''-Dimensional Cumulative Function, And Other Useful Facts About Gaussians and Normal Densities (2009)Code for fitting Gaussians in ImageJ and Fiji.
Exponentials Articles containing proofs Articles with example MATLAB/Octave code
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form
and with parametric extension
for arbitrary real constants , and non-zero . It is named after the mathematician Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refer ...
. The graph of a Gaussian is a characteristic symmetric " bell curve" shape. The parameter is the height of the curve's peak, is the position of the center of the peak, and (the standard deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, whil ...
, sometimes called the Gaussian RMS width) controls the width of the "bell".
Gaussian functions are often used to represent the probability density function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) ca ...
of a normally distributed random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the po ...
with expected value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a ...
and variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbe ...
. In this case, the Gaussian is of the form
Gaussian functions are widely used in statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, indust ...
to describe the normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
s, in signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing '' signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, ...
to define Gaussian filter
In electronics and signal processing mainly in digital signal processing, a Gaussian filter is a filter whose impulse response is a Gaussian function (or an approximation to it, since a true Gaussian response would have infinite impulse res ...
s, in image processing
An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimensio ...
where two-dimensional Gaussians are used for Gaussian blurs, and in mathematics to solve heat equation
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for ...
s and diffusion equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's la ...
s and to define the Weierstrass transform
In mathematics, the Weierstrass transform of a function , named after Karl Weierstrass, is a "smoothed" version of obtained by averaging the values of , weighted with a Gaussian centered at ''x''.
Specifically, it is the function defin ...
.
Properties
Gaussian functions arise by composing theexponential function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, ...
with a concave
Concave or concavity may refer to:
Science and technology
* Concave lens
* Concave mirror
Mathematics
* Concave function, the negative of a convex function
* Concave polygon, a polygon which is not convex
* Concave set
In geometry, a subset o ...
quadratic function
In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before 20th century, the distinction was unclear between a polynomia ...
:
where
*
*
*
The Gaussian functions are thus those functions whose logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 ...
is a concave quadratic function.
The parameter is related to the full width at half maximum (FWHM) of the peak according to
The function may then be expressed in terms of the FWHM, represented by :
Alternatively, the parameter can be interpreted by saying that the two inflection point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case ...
s of the function occur at .
The ''full width at tenth of maximum'' (FWTM) for a Gaussian could be of interest and is
Gaussian functions are analytic
Generally speaking, analytic (from el, ἀναλυτικός, ''analytikos'') refers to the "having the ability to analyze" or "division into elements or principles".
Analytic or analytical can also have the following meanings:
Chemistry
* ...
, and their limit
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2019 ...
as is 0 (for the above case of ).
Gaussian functions are among those functions that are elementary
Elementary may refer to:
Arts, entertainment, and media Music
* ''Elementary'' (Cindy Morgan album), 2001
* ''Elementary'' (The End album), 2007
* ''Elementary'', a Melvin "Wah-Wah Watson" Ragin album, 1977
Other uses in arts, entertainment, a ...
but lack elementary antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolica ...
s; the integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with ...
of the Gaussian function is the error function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a complex function of a complex variable defined as:
:\operatorname z = \frac\int_0^z e^\,\mathrm dt.
This integral is a special (non- elementa ...
. Nonetheless, their improper integrals over the whole real line can be evaluated exactly, using the Gaussian integral
and one obtains
This integral is 1 if and only if (the normalizing constant), and in this case the Gaussian is the probability density function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) ca ...
of a normally distributed random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the po ...
with expected value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a ...
and variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbe ...
:
These Gaussians are plotted in the accompanying figure.
Gaussian functions centered at zero minimize the Fourier uncertainty principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physic ...
.
The product of two Gaussian functions is a Gaussian, and the convolution
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' ...
of two Gaussian functions is also a Gaussian, with variance being the sum of the original variances: . The product of two Gaussian probability density functions (PDFs), though, is not in general a Gaussian PDF.
Taking the Fourier transform (unitary, angular-frequency convention) of a Gaussian function with parameters , and yields another Gaussian function, with parameters , and . So in particular the Gaussian functions with and are kept fixed by the Fourier transform (they are eigenfunction
In mathematics, an eigenfunction of a linear operator ''D'' defined on some function space is any non-zero function f in that space that, when acted upon by ''D'', is only multiplied by some scaling factor called an eigenvalue. As an equation, th ...
s of the Fourier transform with eigenvalue 1).
A physical realization is that of the diffraction pattern: for example, a photographic slide whose transmittance
Transmittance of the surface of a material is its effectiveness in transmitting radiant energy. It is the fraction of incident electromagnetic power that is transmitted through a sample, in contrast to the transmission coefficient, which is t ...
has a Gaussian variation is also a Gaussian function.
The fact that the Gaussian function is an eigenfunction of the continuous Fourier transform allows us to derive the following interesting identity from the Poisson summation formula:
Integral of a Gaussian function
The integral of an arbitrary Gaussian function is An alternative form is where ''f'' must be strictly positive for the integral to converge.Relation to standard Gaussian integral
The integral for some real constants ''a'', ''b'', ''c'' > 0 can be calculated by putting it into the form of a Gaussian integral. First, the constant ''a'' can simply be factored out of the integral. Next, the variable of integration is changed from ''x'' to : and then to : Then, using the Gaussian integral identity we haveTwo-dimensional Gaussian function
 Base form:
In two dimensions, the power to which ''e'' is raised in the Gaussian function is any negative-definite quadratic form. Consequently, the level sets of the Gaussian will always be ellipses.
A particular example of a two-dimensional Gaussian function is
Here the coefficient ''A'' is the amplitude, ''x''0, ''y''0 is the center, and ''σ''''x'', ''σ''''y'' are the ''x'' and ''y'' spreads of the blob. The figure on the right was created using ''A'' = 1, ''x''0 = 0, ''y''0 = 0, ''σ''''x'' = ''σ''''y'' = 1.
The volume under the Gaussian function is given by
In general, a two-dimensional elliptical Gaussian function is expressed as
where the matrix
is positive-definite.
Using this formulation, the figure on the right can be created using , , , .
Base form:
In two dimensions, the power to which ''e'' is raised in the Gaussian function is any negative-definite quadratic form. Consequently, the level sets of the Gaussian will always be ellipses.
A particular example of a two-dimensional Gaussian function is
Here the coefficient ''A'' is the amplitude, ''x''0, ''y''0 is the center, and ''σ''''x'', ''σ''''y'' are the ''x'' and ''y'' spreads of the blob. The figure on the right was created using ''A'' = 1, ''x''0 = 0, ''y''0 = 0, ''σ''''x'' = ''σ''''y'' = 1.
The volume under the Gaussian function is given by
In general, a two-dimensional elliptical Gaussian function is expressed as
where the matrix
is positive-definite.
Using this formulation, the figure on the right can be created using , , , .
Meaning of parameters for the general equation
For the general form of the equation the coefficient ''A'' is the height of the peak and is the center of the blob. If we setthen we rotate the blob by a positive, counter-clockwise angle (for negative, clockwise rotation, invert the signs in the ''b'' coefficient). To get back the coefficients , and from , and use Example rotations of Gaussian blobs can be seen in the following examples: Using the followingOctave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
code, one can easily see the effect of changing the parameters:
image processing
An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimensio ...
and in computational models of visual system
The visual system comprises the sensory organ (the eye) and parts of the central nervous system (the retina containing photoreceptor cells, the optic nerve, the optic tract and the visual cortex) which gives organisms the sense of sight (th ...
function—see the articles on scale space and affine shape adaptation.
Also see multivariate normal distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One ...
.
Higher-order Gaussian or super-Gaussian function
A more general formulation of a Gaussian function with a flat-top and Gaussian fall-off can be taken by raising the content of the exponent to a power : This function is known as a super-Gaussian function and is often used for Gaussian beam formulation. This function may also be expressed in terms of the full width at half maximum (FWHM), represented by : In a two-dimensional formulation, a Gaussian function along and can be combined with potentially different and to form an elliptical Gaussian distribution: or a rectangular Gaussian distribution:Multi-dimensional Gaussian function
In an -dimensional space a Gaussian function can be defined as where is a column of coordinates, is a positive-definite matrix, and denotes matrix transposition. The integral of this Gaussian function over the whole -dimensional space is given as It can be easily calculated by diagonalizing the matrix and changing the integration variables to the eigenvectors of . More generally a shifted Gaussian function is defined as where is the shift vector and the matrix can be assumed to be symmetric, , and positive-definite. The following integrals with this function can be calculated with the same technique: whereEstimation of parameters
A number of fields such as stellar photometry,Gaussian beam
In optics, a Gaussian beam is a beam of electromagnetic radiation with high monochromaticity whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. Thi ...
characterization, and emission/absorption line spectroscopy work with sampled Gaussian functions and need to accurately estimate the height, position, and width parameters of the function. There are three unknown parameters for a 1D Gaussian function (''a'', ''b'', ''c'') and five for a 2D Gaussian function .
The most common method for estimating the Gaussian parameters is to take the logarithm of the data and fit a parabola to the resulting data set.Hongwei Guo, "A simple algorithm for fitting a Gaussian function," IEEE Sign. Proc. Mag. 28(9): 134-137 (2011)./ref> While this provides a simple curve fitting procedure, the resulting algorithm may be biased by excessively weighting small data values, which can produce large errors in the profile estimate. One can partially compensate for this problem through
weighted least squares
Weighted least squares (WLS), also known as weighted linear regression, is a generalization of ordinary least squares and linear regression in which knowledge of the variance of observations is incorporated into the regression.
WLS is also a speci ...
estimation, reducing the weight of small data values, but this too can be biased by allowing the tail of the Gaussian to dominate the fit. In order to remove the bias, one can instead use an iteratively reweighted least squares
The method of iteratively reweighted least squares (IRLS) is used to solve certain optimization problems with objective functions of the form of a ''p''-norm:
:\underset \sum_^n \big, y_i - f_i (\boldsymbol\beta) \big, ^p,
by an iterative met ...
procedure, in which the weights are updated at each iteration.
It is also possible to perform non-linear regression directly on the data, without involving the logarithmic data transformation; for more options, see probability distribution fitting
Probability distribution fitting or simply distribution fitting is the fitting of a probability distribution to a series of data concerning the repeated measurement of a variable phenomenon.
The aim of distribution fitting is to predict the proba ...
.
Parameter precision
Once one has an algorithm for estimating the Gaussian function parameters, it is also important to know howprecise
Precision, precise or precisely may refer to:
Science, and technology, and mathematics Mathematics and computing (general)
* Accuracy and precision, measurement deviation from true value and its scatter
* Significant figures, the number of digit ...
those estimates are. Any least squares
The method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems (sets of equations in which there are more equations than unknowns) by minimizing the sum of the squares of the re ...
estimation algorithm can provide numerical estimates for the variance of each parameter (i.e., the variance of the estimated height, position, and width of the function). One can also use Cramér–Rao bound
In estimation theory and statistics, the Cramér–Rao bound (CRB) expresses a lower bound on the variance of unbiased estimators of a deterministic (fixed, though unknown) parameter, the variance of any such estimator is at least as high as the ...
theory to obtain an analytical expression for the lower bound on the parameter variances, given certain assumptions about the data.N. Hagen, M. Kupinski, and E. L. Dereniak, "Gaussian profile estimation in one dimension," Appl. Opt. 46:5374–5383 (2007)/ref>N. Hagen and E. L. Dereniak, "Gaussian profile estimation in two dimensions," Appl. Opt. 47:6842–6851 (2008)
/ref> # The noise in the measured profile is either i.i.d. Gaussian, or the noise is
Poisson-distributed
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known ...
.
# The spacing between each sampling (i.e. the distance between pixels measuring the data) is uniform.
# The peak is "well-sampled", so that less than 10% of the area or volume under the peak (area if a 1D Gaussian, volume if a 2D Gaussian) lies outside the measurement region.
# The width of the peak is much larger than the distance between sample locations (i.e. the detector pixels must be at least 5 times smaller than the Gaussian FWHM).
When these assumptions are satisfied, the following covariance matrix
In probability theory and statistics, a covariance matrix (also known as auto-covariance matrix, dispersion matrix, variance matrix, or variance–covariance matrix) is a square matrix giving the covariance between each pair of elements of ...
K applies for the 1D profile parameters , , and under i.i.d. Gaussian noise and under Poisson noise:
where is the width of the pixels used to sample the function, is the quantum efficiency of the detector, and indicates the standard deviation of the measurement noise. Thus, the individual variances for the parameters are, in the Gaussian noise case,
and in the Poisson noise case,
For the 2D profile parameters giving the amplitude , position , and width of the profile, the following covariance matrices apply:
where the individual parameter variances are given by the diagonal elements of the covariance matrix.
Discrete Gaussian
digital signal processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are ...
. A simple answer is to sample the continuous Gaussian, yielding the sampled Gaussian kernel. However, this discrete function does not have the discrete analogs of the properties of the continuous function, and can lead to undesired effects, as described in the article scale space implementation.
An alternative approach is to use the discrete Gaussian kernel
In the areas of computer vision, image analysis and signal processing, the notion of scale-space representation is used for processing measurement data at multiple scales, and specifically enhance or suppress image features over different ranges o ...
: Lindeberg, T., "Scale-space for discrete signals," PAMI(12), No. 3, March 1990, pp. 234–254./ref> where denotes the
modified Bessel function
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions of Bessel's differential equation
x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0
for an arbitrary ...
s of integer order.
This is the discrete analog of the continuous Gaussian in that it is the solution to the discrete diffusion equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's la ...
(discrete space, continuous time), just as the continuous Gaussian is the solution to the continuous diffusion equation.
Applications
Gaussian functions appear in many contexts in thenatural sciences
Natural science is one of the branches of science concerned with the description, understanding and prediction of natural phenomena, based on empirical evidence from observation and experimentation. Mechanisms such as peer review and repeat ...
, the social sciences
Social science is one of the branches of science, devoted to the study of societies and the relationships among individuals within those societies. The term was formerly used to refer to the field of sociology, the original "science of so ...
, mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, and engineering
Engineering is the use of scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad range of more speciali ...
. Some examples include:
* In statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, indust ...
and probability theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set ...
, Gaussian functions appear as the density function of the normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
, which is a limiting probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon ...
of complicated sums, according to the central limit theorem
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution even if the original variables themsel ...
.
* Gaussian functions are the Green's function for the (homogeneous and isotropic) diffusion equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's la ...
(and to the heat equation
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for ...
, which is the same thing), a partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
The function is often thought of as an "unknown" to be solved for, similarly to h ...
that describes the time evolution of a mass-density under diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical ...
. Specifically, if the mass-density at time ''t''=0 is given by a Dirac delta, which essentially means that the mass is initially concentrated in a single point, then the mass-distribution at time ''t'' will be given by a Gaussian function, with the parameter ''a'' being linearly related to 1/ and ''c'' being linearly related to ; this time-varying Gaussian is described by the heat kernel
In the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a specified domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectr ...
. More generally, if the initial mass-density is φ(''x''), then the mass-density at later times is obtained by taking the convolution
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' ...
of φ with a Gaussian function. The convolution of a function with a Gaussian is also known as a Weierstrass transform
In mathematics, the Weierstrass transform of a function , named after Karl Weierstrass, is a "smoothed" version of obtained by averaging the values of , weighted with a Gaussian centered at ''x''.
Specifically, it is the function defin ...
.
* A Gaussian function is the wave function
A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements ...
of the ground state
The ground state of a quantum-mechanical system is its stationary state of lowest energy; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state. ...
of the quantum harmonic oscillator
量子調和振動子 は、 古典調和振動子 の 量子力学 類似物です。任意の滑らかな ポテンシャル は通常、安定した 平衡点 の近くで 調和ポテンシャル として近似できるため、最� ...
.
* The molecular orbital
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of find ...
s used in computational chemistry
Computational chemistry is a branch of chemistry that uses computer simulation to assist in solving chemical problems. It uses methods of theoretical chemistry, incorporated into computer programs, to calculate the structures and properties of mo ...
can be linear combinations of Gaussian functions called Gaussian orbital In computational chemistry and molecular physics, Gaussian orbitals (also known as Gaussian type orbitals, GTOs or Gaussians) are functions used as atomic orbitals in the LCAO method for the representation of electron orbitals in molecules an ...
s (see also basis set (chemistry)
In theoretical and computational chemistry, a basis set is a set of functions (called basis functions) that is used to represent the electronic wave function in the Hartree–Fock method or density-functional theory in order to turn the pa ...
).
* Mathematically, the derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
s of the Gaussian function can be represented using Hermite functions
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
The polynomials arise in:
* signal processing as Hermitian wavelets for wavelet transform analysis
* probability, such as the Edgeworth series, as well as ...
. For unit variance, the ''n''-th derivative of the Gaussian is the Gaussian function itself multiplied by the ''n''-th Hermite polynomial, up to scale.
* Consequently, Gaussian functions are also associated with the vacuum state in quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and ...
.
* Gaussian beam
In optics, a Gaussian beam is a beam of electromagnetic radiation with high monochromaticity whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. Thi ...
s are used in optical systems, microwave systems and lasers.
* In scale space representation, Gaussian functions are used as smoothing kernels for generating multi-scale representations in computer vision
Computer vision is an interdisciplinary scientific field that deals with how computers can gain high-level understanding from digital images or videos. From the perspective of engineering, it seeks to understand and automate tasks that the human ...
and image processing
An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimensio ...
. Specifically, derivatives of Gaussians (Hermite functions
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
The polynomials arise in:
* signal processing as Hermitian wavelets for wavelet transform analysis
* probability, such as the Edgeworth series, as well as ...
) are used as a basis for defining a large number of types of visual operations.
* Gaussian functions are used to define some types of artificial neural network
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains.
An ANN is based on a collection of connected unit ...
s.
* In fluorescence microscopy a 2D Gaussian function is used to approximate the Airy disk, describing the intensity distribution produced by a point source.
* In signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing '' signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, ...
they serve to define Gaussian filter
In electronics and signal processing mainly in digital signal processing, a Gaussian filter is a filter whose impulse response is a Gaussian function (or an approximation to it, since a true Gaussian response would have infinite impulse res ...
s, such as in image processing
An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimensio ...
where 2D Gaussians are used for Gaussian blurs. In digital signal processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are ...
, one uses a discrete Gaussian kernel
In the areas of computer vision, image analysis and signal processing, the notion of scale-space representation is used for processing measurement data at multiple scales, and specifically enhance or suppress image features over different ranges o ...
, which may be defined by sampling a Gaussian, or in a different way.
* In geostatistics
Geostatistics is a branch of statistics focusing on spatial or spatiotemporal datasets. Developed originally to predict probability distributions of ore grades for mining operations, it is currently applied in diverse disciplines including pe ...
they have been used for understanding the variability between the patterns of a complex training image. They are used with kernel methods to cluster the patterns in the feature space.Honarkhah, M and Caers, J, 2010, Stochastic Simulation of Patterns Using Distance-Based Pattern Modeling
', Mathematical Geosciences, 42: 487–517
See also
*Normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
* Lorentzian function
* Radial basis function kernel
References
External links
Mathworld, includes a proof for the relations between c and FWHM
* {{MathPages, id=home/kmath045/kmath045, title=Integrating The Bell Curve
Haskell, Erlang and Perl implementation of Gaussian distribution
Bensimhoun Michael, ''N''-Dimensional Cumulative Function, And Other Useful Facts About Gaussians and Normal Densities (2009)
Exponentials Articles containing proofs Articles with example MATLAB/Octave code