differential privacy

Differential privacy (DP) is a mathematically rigorous framework for releasing statistical information about datasets while protecting the privacy of individual data subjects. It enables a data holder to share aggregate patterns of the group while limiting information that is leaked about specific individuals. This is done by injecting carefully calibrated noise into statistical computations such that the utility of the statistic is preserved while provably limiting what can be inferred about any individual in the dataset.

Another way to describe differential privacy is as a constraint on the algorithms used to publish aggregate information about a statistical database which limits the disclosure of private information of records in the database. For example, differentially private algorithms are used by some government agencies to publish demographic information or other statistical aggregates while ensuring confidentiality of survey responses, and by companies to collect information about user behavior while controlling what is visible even to internal analysts.

Roughly, an algorithm is differentially private if an observer seeing its output cannot tell whether a particular individual's information was used in the computation. Differential privacy is often discussed in the context of identifying individuals whose information may be in a database. Although it does not directly refer to identification and reidentification attacks, differentially private algorithms provably resist such attacks.Calibrating Noise to Sensitivity in Private Data Analysis
by Cynthia Dwork, Frank McSherry, Kobbi Nissim, Adam Smith. In Theory of Cryptography Conference (TCC), Springer, 2006. . Th
full version
appears in Journal of Privacy and Confidentiality, 7 (3), 17-51.

ε-differential privacy

The 2006 Cynthia Dwork, Frank McSherry, Kobbi Nissim, and Adam D. Smith article introduced the concept of ε-differential privacy, a mathematical definition for the privacy loss associated with any data release drawn from a statistical database. (Here, the term ''statistical database'' means a set of data that are collected under the pledge of confidentiality for the purpose of producing statistics that, by their production, do not compromise the privacy of those individuals who provided the data.)

The definition of ε-differential privacy requires that a change to one entry in a database only creates a small change in the probability distribution of the outputs of measurements, as seen by the attacker. The intuition for the definition of ε-differential privacy is that a person's privacy cannot be compromised by a statistical release if their data are not in the database. In differential privacy, each individual is given roughly the same privacy that would result from having their data removed. That is, the statistical functions run on the database should not be substantially affected by the removal, addition, or change of any individual in the data.

How much any individual contributes to the result of a database query depends in part on how many people's data are involved in the query. If the database contains data from a single person, that person's data contributes 100%. If the database contains data from a hundred people, each person's data contributes just 1%. The key insight of differential privacy is that as the query is made on the data of fewer and fewer people, more noise needs to be added to the query result to produce the same amount of privacy. Hence the name of the 2006 paper, "Calibrating noise to sensitivity in private data analysis."

Definition

Let ε be a positive real number and $\mathcal$ be a randomized algorithm that takes a dataset as input (representing the actions of the trusted party holding the data). Let $\textrm\ \mathcal$ denote the image of $\mathcal$.

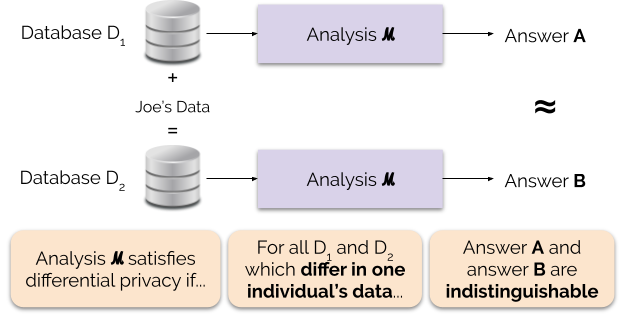
The algorithm $\mathcal$ is said to provide (ε, δ)-differential privacy if, for all datasets $D_1$ and $D_2$ that differ on a single element (i.e., the data of one person), and all subsets $S$ of $\textrm\ \mathcal$:

where the probability is taken over the randomness used by the algorithm.The Algorithmic Foundations of Differential Privacy
by Cynthia Dwork and Aaron Roth. Foundations and Trends in Theoretical Computer Science. Vol. 9, no. 3–4, pp. 211‐407, Aug. 2014. This definition is sometimes called "approximate differential privacy", with "pure differential privacy" being a special case when $\delta = 0$. In the latter case, the algorithm is commonly said to satisfy ε-differential privacy (i.e., omitting $\delta = 0$).

Differential privacy offers strong and robust guarantees that facilitate modular design and analysis of differentially private mechanisms due to its composability, robustness to post-processing, and graceful degradation in the presence of correlated data.

Example

According to this definition, differential privacy is a condition on the release mechanism (i.e., the trusted party releasing information ''about'' the dataset) and not on the dataset itself. Intuitively, this means that for any two datasets that are similar, a given differentially private algorithm will behave approximately the same on both datasets. The definition gives a strong guarantee that presence or absence of an individual will not affect the final output of the algorithm significantly.

For example, assume we have a database of medical records $D_1$ where each record is a pair (Name, X), where $X$ is a Boolean denoting whether a person has diabetes or not. For example:

Now suppose a malicious user (often termed an ''adversary'') wants to find whether Chandler has diabetes or not. Suppose he also knows in which row of the database Chandler resides. Now suppose the adversary is only allowed to use a particular form of query $Q_i$ that returns the partial sum of the first $i$ rows of column $X$ in the database. In order to find Chandler's diabetes status the adversary executes $Q_5(D_1)$ and $Q_4(D_1)$, then computes their difference. In this example, $Q_5(D_1) = 3$ and $Q_4(D_1) = 2$, so their difference is 1. This indicates that the "Has Diabetes" field in Chandler's row must be 1. This example highlights how individual information can be compromised even without explicitly querying for the information of a specific individual.

Continuing this example, if we construct $D_2$ by replacing (Chandler, 1) with (Chandler, 0) then this malicious adversary will be able to distinguish $D_2$ from $D_1$ by computing $Q_5 - Q_4$ for each dataset. If the adversary were required to receive the values $Q_i$ via an $\varepsilon$-differentially private algorithm, for a sufficiently small $\varepsilon$, then he or she would be unable to distinguish between the two datasets.

Composability and robustness to post processing

Composability refers to the fact that the joint distribution of the outputs of (possibly adaptively chosen) differentially private mechanisms satisfies differential privacy.

* Sequential composition. If we query an ε-differential privacy mechanism $t$ times, and the randomization of the mechanism is independent for each query, then the result would be $\varepsilon t$-differentially private. In the more general case, if there are $n$ independent mechanisms: $\mathcal_1,\dots,\mathcal_n$, whose privacy guarantees are $\varepsilon_1,\dots,\varepsilon_n$ differential privacy, respectively, then any function $g$ of them: $g(\mathcal_1,\dots,\mathcal_n)$ is $\left(\sum\limits_^ \varepsilon_i\right)$-differentially private.Privacy integrated queries: an extensible platform for privacy-preserving data analysis
by Frank D. McSherry. In Proceedings of the 35th SIGMOD International Conference on Management of Data (SIGMOD), 2009.

* Parallel composition. If the previous mechanisms are computed on ''disjoint'' subsets of the private database then the function $g$ would be $(\max_i \varepsilon_i)$-differentially private instead.

The other important property for modular use of differential privacy is robustness to post processing. This is defined to mean that for any deterministic or randomized function $F$ defined over the image of the mechanism $\mathcal$, if $\mathcal$ satisfies ε-differential privacy, so does $F(\mathcal)$.

The property of composition permits modular construction and analysis of differentially private mechanisms and motivates the concept of the ''privacy loss budget''. If all elements that access sensitive data of a complex mechanisms are separately differentially private, so will be their combination, followed by arbitrary post-processing.

Group privacy

In general, ε-differential privacy is designed to protect the privacy between neighboring databases which differ only in one row. This means that no adversary with arbitrary auxiliary information can know if one particular participant submitted their information. However this is also extendable. We may want to protect databases differing in $c$ rows, which amounts to an adversary with arbitrary auxiliary information knowing if $c$ particular participants submitted their information. This can be achieved because if $c$ items change, the probability dilation is bounded by $\exp ( \varepsilon c )$ instead of $\exp ( \varepsilon )$,Differential Privacy
by Cynthia Dwork, International Colloquium on Automata, Languages and Programming (ICALP) 2006, p. 1–12. i.e., for D₁ and D₂ differing on $c$ items:\Pr mathcal(D_)\in Sleq
\exp(\varepsilon c)\cdot\Pr mathcal(D_)\in S,\!Thus setting ε instead to $\varepsilon/c$ achieves the desired result (protection of $c$ items). In other words, instead of having each item ε-differentially private protected, now every group of $c$ items is ε-differentially private protected (and each item is $(\varepsilon/c)$-differentially private protected).

Hypothesis testing interpretation

One can think of differential privacy as bounding the error rates in a hypothesis test. Consider two hypotheses:

* $H_0$: The individual's data is not in the dataset.

* $H_1$: The individual's data is in the dataset.

Then, there are two error rates:

* False Positive Rate (FPR): P_\text = \Pr text H_1 \mid H_0 \text

* False Negative Rate (FNR): P_\text = \Pr text H_0 \mid H_1 \text

Ideal protection would imply that both error rates are equal, but for a fixed (ε, δ) setting, an attacker can achieve the following rates:

* $\$

ε-differentially private mechanisms

Since differential privacy is a probabilistic concept, any differentially private mechanism is necessarily randomized. Some of these, like the Laplace mechanism, described below, rely on adding controlled noise to the function that we want to compute. Others, like the exponential mechanism and posterior sampling sample from a problem-dependent family of distributions instead.

An important definition with respect to ε-differentially private mechanisms is sensitivity. Let $d$ be a positive integer, $\mathcal$ be a collection of datasets, and $f \colon \mathcal \rightarrow \mathbb^d$ be a function. One definition of the ''sensitivity'' of a function, denoted $\Delta f$, can be defined by:$\Delta f=\max \lVert f(D_1)-f(D_2) \rVert_1,$where the maximum is over all pairs of datasets $D_1$ and $D_2$ in $\mathcal$ differing in at most one element and $\lVert \cdot \rVert_1$ denotes the L1 norm. In the example of the medical database below, if we consider $f$ to be the function $Q_i$, then the sensitivity of the function is one, since changing any one of the entries in the database causes the output of the function to change by either zero or one. This can be generalized to other metric spaces (measures of distance), and must be to make certain differentially private algorithms work, including adding noise from the Gaussian distribution (which requires the L2 norm) instead of the Laplace distribution.

There are techniques (which are described below) using which we can create a differentially private algorithm for functions, with parameters that vary depending on their sensitivity.

Laplace mechanism

The Laplace mechanism adds Laplace noise (i.e. noise from the Laplace distribution, which can be expressed by probability density function $\text(y)\propto \exp(-, y, /\lambda)\,\!$, which has mean zero and standard deviation $\sqrt \lambda\,\!$). Now in our case we define the output function of $\mathcal\,\!$ as a real valued function (called as the transcript output by $\mathcal\,\!$) as $\mathcal_(x)=f(x)+Y\,\!$ where $Y \sim \text(\lambda)\,\!\,\!$ and $f\,\!$ is the original real valued query/function we planned to execute on the database. Now clearly $\mathcal_(x)\,\!$ can be considered to be a continuous random variable, where
:$\frac=\frac\,\!$

which is at most $e^\leq e^\,\!$. We can consider $\frac\,\!$ to be the privacy factor $\varepsilon\,\!$. Thus $\mathcal\,\!$ follows a differentially private mechanism (as can be seen from the definition above). If we try to use this concept in our diabetes example then it follows from the above derived fact that in order to have $\mathcal\,\!$ as the $\varepsilon\,\!$-differential private algorithm we need to have $\lambda=1/\varepsilon\,\!$. Though we have used Laplace noise here, other forms of noise, such as the Gaussian Noise, can be employed, but they may require a slight relaxation of the definition of differential privacy.

Randomized response

A simple example, especially developed in the social sciences, is to ask a person to answer the question "Do you own the ''attribute A''?", according to the following procedure:

# Toss a coin.
# If heads, then toss the coin again (ignoring the outcome), and answer the question honestly.
# If tails, then toss the coin again and answer "Yes" if heads, "No" if tails.

(The seemingly redundant extra toss in the first case is needed in situations where just the ''act'' of tossing a coin may be observed by others, even if the actual result stays hidden.) The confidentiality then arises from the refutability of the individual responses.

But, overall, these data with many responses are significant, since positive responses are given to a quarter by people who do not have the ''attribute A'' and three-quarters by people who actually possess it. Thus, if ''p'' is the true proportion of people with ''A'', then we expect to obtain (1/4)(1-''p'') + (3/4)''p'' = (1/4) + ''p''/2 positive responses. Hence it is possible to estimate ''p''.

In particular, if the ''attribute A'' is synonymous with illegal behavior, then answering "Yes" is not incriminating, insofar as the person has a probability of a "Yes" response, whatever it may be.

Although this example, inspired by randomized response, might be applicable to microdata (i.e., releasing datasets with each individual response), by definition differential privacy excludes microdata releases and is only applicable to queries (i.e., aggregating individual responses into one result) as this would violate the requirements, more specifically the plausible deniability that a subject participated or not.

Stable transformations

A transformation $T$ is $c$-stable if the Hamming distance between $T(A)$ and $T(B)$ is at most $c$-times the Hamming distance between $A$ and $B$ for any two databases $A,B$. If there is a mechanism $M$ that is $\varepsilon$-differentially private, then the composite mechanism $M\circ T$ is $(\varepsilon \times c)$-differentially private.

This could be generalized to group privacy, as the group size could be thought of as the Hamming distance $h$ between
$A$ and $B$ (where $A$ contains the group and $B$ does not). In this case $M\circ T$ is $(\varepsilon \times c \times h)$-differentially private.

Research

Early research leading to differential privacy

In 1977, Tore Dalenius formalized the mathematics of cell suppression. Tore Dalenius was a Swedish statistician who contributed to statistical privacy through his 1977 paper that revealed a key point about statistical databases, which was that databases should not reveal information about an individual that is not otherwise accessible. He also defined a typology for statistical disclosures.

In 1979, Dorothy Denning, Peter J. Denning and Mayer D. Schwartz formalized the concept of a Tracker, an adversary that could learn the confidential contents of a statistical database by creating a series of targeted queries and remembering the results. This and future research showed that privacy properties in a database could only be preserved by considering each new query in light of (possibly all) previous queries. This line of work is sometimes called ''query privacy,'' with the final result being that tracking the impact of a query on the privacy of individuals in the database was NP-hard.

21st century

In 2003, Kobbi Nissim and Irit Dinur demonstrated that it is impossible to publish arbitrary queries on a private statistical database without revealing some amount of private information, and that the entire information content of the database can be revealed by publishing the results of a surprisingly small number of random queries—far fewer than was implied by previous work. The general phenomenon is known as the Fundamental Law of Information Recovery, and its key insight, namely that in the most general case, privacy cannot be protected without injecting some amount of noise, led to development of differential privacy.

In 2006, Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam D. Smith published an article formalizing the amount of noise that needed to be added and proposing a generalized mechanism for doing so. This paper also created the first formal definition of differential privacy. Their work was a co-recipient of the 2016 TCC Test-of-Time Award and the 2017 Gödel Prize.

Since then, subsequent research has shown that there are many ways to produce very accurate statistics from the database while still ensuring high levels of privacy.

Adoption in real-world applications

To date there are over 12 real-world deployments of differential privacy, the most noteworthy being:
* 2008: U.S. Census Bureau, for showing commuting patterns.Ashwin Machanavajjhala, Daniel Kifer, John M. Abowd, Johannes Gehrke, and Lars Vilhuber. "Privacy: Theory meets Practice on the Map". In Proceedings of the 24th International Conference on Data Engineering, ICDE) 2008.
* 2014: Google's RAPPOR, for telemetry such as learning statistics about unwanted software hijacking users' settings.
* 2015: Google, for sharing historical traffic statistics.Tackling Urban Mobility with Technology
by Andrew Eland. Google Policy Europe Blog, Nov 18, 2015.
* 2016: Apple iOS 10, for use in Intelligent personal assistant technology.
* 2017: Microsoft, for telemetry in Windows.Collecting telemetry data privately
by Bolin Ding, Jana Kulkarni, Sergey Yekhanin. NIPS 2017.
* 2020
Social Science One
and Facebook, a 55 trillion cell dataset for researchers to learn about elections and democracy.
* 2021: The US Census Bureau uses differential privacy to release redistricting data from the 2020 Census.

Public purpose considerations

There are several public purpose considerations regarding differential privacy that are important to consider, especially for policymakers and policy-focused audiences interested in the social opportunities and risks of the technology:

* Data utility and accuracy. The main concern with differential privacy is the trade-off between data utility and individual privacy. If the privacy loss parameter is set to favor utility, the privacy benefits are lowered (less “noise” is injected into the system); if the privacy loss parameter is set to favor heavy privacy, the accuracy and utility of the dataset are lowered (more “noise” is injected into the system). It is important for policymakers to consider the trade-offs posed by differential privacy in order to help set appropriate best practices and standards around the use of this privacy preserving practice, especially considering the diversity in organizational use cases. It is worth noting, though, that decreased accuracy and utility is a common issue among all statistical disclosure limitation methods and is not unique to differential privacy. What is unique, however, is how policymakers, researchers, and implementers can consider mitigating against the risks presented through this trade-off.
* Data privacy and security. Differential privacy provides a quantified measure of privacy loss and an upper bound and allows curators to choose the explicit trade-off between privacy and accuracy. It is robust to still unknown privacy attacks. However, it encourages greater data sharing, which if done poorly, increases privacy risk. Differential privacy implies that privacy is protected, but this depends very much on the privacy loss parameter chosen and may instead lead to a false sense of security. Finally, though it is robust against unforeseen future privacy attacks, a countermeasure may be devised that we cannot predict.

Attacks in practice

Because differential privacy techniques are implemented on real computers, they are vulnerable to various attacks not possible to compensate for solely in the mathematics of the techniques themselves. In addition to standard defects of software artifacts that can be identified using testing or fuzzing, implementations of differentially private mechanisms may suffer from the following vulnerabilities:

* Subtle algorithmic or analytical mistakes.
* Timing side-channel attacks. In contrast with timing attacks against implementations of cryptographic algorithms that typically have low leakage rate and must be followed with non-trivial cryptanalysis, a timing channel may lead to a catastrophic compromise of a differentially private system, since a targeted attack can be used to exfiltrate the very bit that the system is designed to hide.
* Leakage through floating-point arithmetic. Differentially private algorithms are typically presented in the language of probability distributions, which most naturally lead to implementations using floating-point arithmetic. The abstraction of floating-point arithmetic is leaky, and without careful attention to details, a naive implementation may fail to provide differential privacy. (This is particularly the case for ε-differential privacy, which does not allow any probability of failure, even in the worst case.) For example, the support of a textbook sampler of the Laplace distribution (required, for instance, for the Laplace mechanism) is less than 80% of all double-precision floating point numbers; moreover, the support for distributions with different means are not identical. A single sample from a naïve implementation of the Laplace mechanism allows distinguishing between two adjacent datasets with probability more than 35%.
* Timing channel through floating-point arithmetic. Unlike operations over integers that are typically constant-time on modern CPUs, floating-point arithmetic exhibits significant input-dependent timing variability. Handling of subnormals can be particularly slow, as much as by ×100 compared to the typical case.

See also

* Implementations of differentially private analyses – deployments of differential privacy
* Quasi-identifier
* Exponential mechanism (differential privacy) – a technique for designing differentially private algorithms
* k-anonymity
* Differentially private analysis of graphs
* Protected health information
* Local differential privacy
*Privacy
* Differential privacy composition theorems

References

Further reading

Publications

Calibrating noise to sensitivity in private data analysis
Cynthia Dwork, Frank McSherry, Kobbi Nissim, and Adam Smith. 2006. In Proceedings of the Third conference on Theory of Cryptography (TCC'06). Springer-Verlag, Berlin, Heidelberg, 265–284. https://doi.org/10.1007/11681878_14 (This is the original publication of Differential Privacy, and not the eponymous article by Dwork that was published the same year.)

Differential Privacy: A Survey of Results
by Cynthia Dwork, Microsoft Research, April 2008 (Presents what was discovered during the first two years of research on differential privacy.)

Differential Privacy: A Primer for a Non-Technical Audience
Alexandra Wood, Micah Altman, Aaron Bembenek, Mark Bun, Marco Gaboardi, et al, Vanderbilt Journal of Entertainment & Technology LawVanderbilt Journal of Entertainment, Volume 21, Issue 1, Fall 2018. (A good introductory document, but definitely *not* for non-technical audiences!)

Technology Factsheet: Differential Privacy
by Raina Gandhi and Amritha Jayanti, Belfer Center for Science and International Affairs, Fall 2020

Differential Privacy and the 2020 US Census
MIT Case Studies in Social and Ethical Responsibilities of Computing, no. Winter 2022 (January). https://doi.org/10.21428/2c646de5.7ec6ab93.
* {{open access
* Bowen, Claire McKay and Simson Garfinkel
The Philosophy of Differential Privacy
AMS Notices, November 2021.

Tutorials

A Practical Beginner's Guide To Differential Privacy
by Christine Task, Purdue University, April 2012

Theory of cryptography
Information privacy