 |
Huffman Coding
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Doctor of Science, Sc.D. student at Massachusetts Institute of Technology, MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes". The output from Huffman's algorithm can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). The algorithm derives this table from the estimated probability or frequency of occurrence (''weight'') for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman's method can be efficiently implemented, finding a code in time linear time, linear to the number of input weigh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
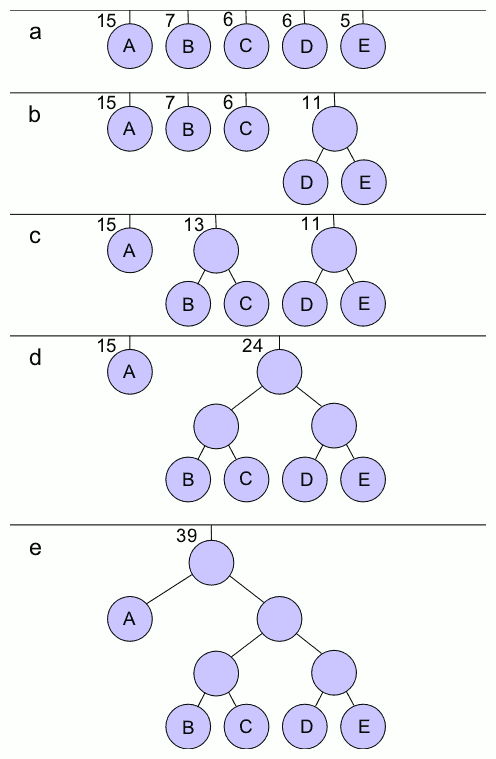
Huffman Tree 2
Huffman may refer to: __NOTOC__ Places United States * Huffman, Indiana, an unincorporated community * Huffman, Texas, an unincorporated community * Huffman, Virginia, an unincorporated community * Huffman, West Virginia, an unincorporated community Antarctica * Mount Huffman, Ellsworth Land People * Huffman (surname), a surname * Huffman Eja-Tabe (born 1981), Cameroonian footballer in North America Other uses * Elkhart Motor Truck Company, Huffman Brothers Motor Company, 1920s Indiana-based car company' * Huffman High School, Birmingham, Alabama * Huffman Manufacturing Company, former name of the Huffy Corporation, a bicycle manufacturer based in Dayton, Ohio * Mount Huffman (Texas), a mountain in Big Bend National Park, USA See also * Huffman coding, a data compression algorithm (''Huffman tree'') by David A. Huffman * Huffman Dam, near Fairborn, Ohio * Huffman Historic District, Dayton, Ohio, on the National Register of Historic Places * Huffman Prairie, Ohio, also known as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Term Paper
A term paper is a research paper written by students over an academic term, accounting for a large part of a grade. Merriam-Webster defines it as "a major written assignment in a school or college course representative of a student's achievement during a term". Term papers are generally intended to describe an event, a concept, or argue a point. It is a written original work discussing a topic in detail, usually several typed pages in length, and is often due at the end of a semester. There is much overlap between the terms: ''research paper'' and ''term paper''. A ''term paper'' was originally a written assignment (usually a research based paper) that was due at the end of the "term"—either a semester or quarter, depending on which unit of measure a school used. However, not all term papers involve academic research, and not all research papers are term papers. History Term papers date back to the beginning of the 19th century when print could be reproduced cheaply and written ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Information Entropy
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to , 1/math>, the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
A Mathematical Theory Of Communication
"A Mathematical Theory of Communication" is an article by mathematician Claude E. Shannon published in '' Bell System Technical Journal'' in 1948. It was renamed ''The Mathematical Theory of Communication'' in the 1949 book of the same name, a small but significant title change after realizing the generality of this work. It has tens of thousands of citations, being one of the most influential and cited scientific papers of all time, as it gave rise to the field of information theory, with ''Scientific American'' referring to the paper as the "Magna Carta of the Information Age", while the electrical engineer Robert G. Gallager called the paper a "blueprint for the digital era". Historian James Gleick rated the paper as the most important development of 1948, placing the transistor second in the same time period, with Gleick emphasizing that the paper by Shannon was "even more profound and more fundamental" than the transistor. It is also noted that "as did relativity and qua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Variable-length Code
In coding theory, a variable-length code is a code which maps source symbols to a ''variable'' number of bits. The equivalent concept in computer science is '' bit string''. Variable-length codes can allow sources to be compressed and decompressed with ''zero'' error (lossless data compression) and still be read back symbol by symbol. With the right coding strategy, an independent and identically-distributed source may be compressed almost arbitrarily close to its entropy. This is in contrast to fixed-length coding methods, for which data compression is only possible for large blocks of data, and any compression beyond the logarithm of the total number of possibilities comes with a finite (though perhaps arbitrarily small) probability of failure. Some examples of well-known variable-length coding strategies are Huffman coding, Lempel–Ziv coding, arithmetic coding, and context-adaptive variable-length coding. Codes and their extensions The extension of a code is the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Shannon Entropy
Shannon may refer to: People * Shannon (given name) * Shannon (surname) * Shannon (American singer), stage name of singer Brenda Shannon Greene (born 1958) * Shannon (South Korean singer), British-South Korean singer and actress Shannon Arrum Williams (born 1998) * Shannon, intermittent stage name of English singer-songwriter Marty Wilde (born 1939) Places Australia * Shannon, Tasmania, a locality * Hundred of Shannon, a cadastral unit in South Australia * Shannon, a former name for the area named Calomba, South Australia since 1916 * Shannon River (Western Australia) * Shannon, Western Australia, a locality in the Shire of Manjimup * Shannon National Park, a national park in Western Australia Canada * Shannon, New Brunswick, a community * Shannon, Quebec, a city * Shannon Bay, former name of Darrell Bay, British Columbia * Shannon Falls, a waterfall in British Columbia Ireland * River Shannon, the longest river in Ireland ** Shannon Cave, a subterranean section o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Weighted Path Length From The Root
A weight function is a mathematical device used when performing a sum, integral, or average to give some elements more "weight" or influence on the result than other elements in the same set. The result of this application of a weight function is a weighted sum or weighted average. Weight functions occur frequently in statistics and analysis, and are closely related to the concept of a measure. Weight functions can be employed in both discrete and continuous settings. They can be used to construct systems of calculus called "weighted calculus" and "meta-calculus".Jane Grossma''Meta-Calculus: Differential and Integral'' , 1981. Discrete weights General definition In the discrete setting, a weight function w \colon A \to \R^+ is a positive function defined on a discrete set A, which is typically finite or countable. The weight function w(a) := 1 corresponds to the ''unweighted'' situation in which all elements have equal weight. One can then apply this weight to various conce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Prefix Code
A prefix code is a type of code system distinguished by its possession of the prefix property, which requires that there is no whole Code word (communication), code word in the system that is a prefix (computer science), prefix (initial segment) of any other code word in the system. It is trivially true for fixed-length codes, so only a point of consideration for variable-length code, variable-length codes. For example, a code with code has the prefix property; a code consisting of does not, because "5" is a prefix of "59" and also of "55". A prefix code is a uniquely decodable code: given a complete and accurate sequence, a receiver can identify each word without requiring a special marker between words. However, there are uniquely decodable codes that are not prefix codes; for instance, the reverse of a prefix code is still uniquely decodable (it is a suffix code), but it is not necessarily a prefix code. Prefix codes are also known as prefix-free codes, prefix condition codes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Pearson Education
Pearson Education, known since 2011 as simply Pearson, is the educational publishing and services subsidiary of the international corporation Pearson plc. The subsidiary was formed in 1998, when Pearson plc acquired Simon & Schuster's educational business and combined it with Pearson's existing education company Addison-Wesley Longman. Pearson Education was restyled as simply Pearson in 2011. In 2016, the diversified parent corporation Pearson plc rebranded to focus entirely on education publishing and services; further, as of 2023, Pearson Education is Pearson plc's main subsidiary. In 2019, Pearson Education began phasing out the prominence of its hard-copy textbooks in favor of digital textbooks, which cost the company far less, and can be updated frequently and easily. As of 2023, Pearson Education has testing/teaching centers in over 55 countries worldwide; the UK and the U.S. have the most centers. The headquarters of parent company Pearson plc are in London, England. P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Shannon–Fano Coding
In the field of data compression, Shannon–Fano coding, named after Claude Shannon and Robert Fano, is one of two related techniques for constructing a prefix code based on a set of symbols and their probabilities (estimated or measured). * Shannon's method chooses a prefix code where a source symbol i is given the codeword length l_i = \lceil - \log_2 p_i\rceil. One common way of choosing the codewords uses the binary expansion of the cumulative probabilities. This method was proposed in Shannon's "A Mathematical Theory of Communication" (1948), his article introducing the field of information theory. * Fano's method divides the source symbols into two sets ("0" and "1") with probabilities as close to 1/2 as possible. Then those sets are themselves divided in two, and so on, until each set contains only one symbol. The codeword for that symbol is the string of "0"s and "1"s that records which half of the divides it fell on. This method was proposed in a later (in print) technica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |