Huffman coding

In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code proceeds by means of Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes".

The output from Huffman's algorithm can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). The algorithm derives this table from the estimated probability or frequency of occurrence (''weight'') for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman's method can be efficiently implemented, finding a code in time linear to the number of input weights if these weights are sorted. However, although optimal among methods encoding symbols separately, Huffman coding is not always optimal among all compression methods - it is replaced with arithmetic coding or asymmetric numeral systemsJ. Duda, K. Tahboub, N. J. Gadil, E. J. Delp, ''The use of asymmetric numeral systems as an accurate replacement for Huffman coding''
Picture Coding Symposium, 2015. if a better compression ratio is required.

History

In 1951, David A. Huffman and his MIT information theory classmates were given the choice of a term paper or a final exam. The professor, Robert M. Fano, assigned a term paper on the problem of finding the most efficient binary code. Huffman, unable to prove any codes were the most efficient, was about to give up and start studying for the final when he hit upon the idea of using a frequency-sorted binary tree and quickly proved this method the most efficient.

In doing so, Huffman outdid Fano, who had worked with Claude Shannon to develop a similar code. Building the tree from the bottom up guaranteed optimality, unlike the top-down approach of Shannon–Fano coding.

Terminology

Huffman coding uses a specific method for choosing the representation for each symbol, resulting in a prefix code (sometimes called "prefix-free codes", that is, the bit string representing some particular symbol is never a prefix of the bit string representing any other symbol). Huffman coding is such a widespread method for creating prefix codes that the term "Huffman code" is widely used as a synonym for "prefix code" even when such a code is not produced by Huffman's algorithm.

Problem definition

Informal description

;Given: A set of symbols and their weights (usually proportional to probabilities).
;Find: A prefix-free binary code (a set of codewords) with minimum expected codeword length (equivalently, a tree with minimum weighted path length from the root).

Formalized description

Input.

Alphabet $A = (a_,a_,\dots,a_)$, which is the symbol alphabet of size $n$.

Tuple $W = (w_,w_,\dots,w_)$, which is the tuple of the (positive) symbol weights (usually proportional to probabilities), i.e. $w_ = \operatorname\left(a_\right),\, i \in \$.



Output.

Code $C\left(W\right) = (c_,c_,\dots,c_)$, which is the tuple of (binary) codewords, where $c_$ is the codeword for $a_,\, i \in \$.



Goal.

Let $L\left(C\left(W\right)\right) = \sum_^$ be the weighted path length of code $C$. Condition: $L\left(C\left(W\right)\right) \leq L\left(T\left(W\right)\right)$ for any code $T\left(W\right)$.

Example

We give an example of the result of Huffman coding for a code with five characters and given weights. We will not verify that it minimizes ''L'' over all codes, but we will compute ''L'' and compare it to the Shannon entropy ''H'' of the given set of weights; the result is nearly optimal.

For any code that is ''biunique'', meaning that the code is ''uniquely decodeable'', the sum of the probability budgets across all symbols is always less than or equal to one. In this example, the sum is strictly equal to one; as a result, the code is termed a ''complete'' code. If this is not the case, one can always derive an equivalent code by adding extra symbols (with associated null probabilities), to make the code complete while keeping it ''biunique''.

As defined by Shannon (1948), the information content ''h'' (in bits) of each symbol ''a''_i with non-null probability is

:$h(a_i) = \log_2.$

The entropy ''H'' (in bits) is the weighted sum, across all symbols with non-zero probability , of the information content of each symbol:

:$H(A) = \sum_ w_i h(a_i) = \sum_ w_i \log_2 = - \sum_ w_i \log_2.$

(Note: A symbol with zero probability has zero contribution to the entropy, since $\lim_ w \log_2 w = 0$. So for simplicity, symbols with zero probability can be left out of the formula above.)

As a consequence of Shannon's source coding theorem, the entropy is a measure of the smallest codeword length that is theoretically possible for the given alphabet with associated weights. In this example, the weighted average codeword length is 2.25 bits per symbol, only slightly larger than the calculated entropy of 2.205 bits per symbol. So not only is this code optimal in the sense that no other feasible code performs better, but it is very close to the theoretical limit established by Shannon.

In general, a Huffman code need not be unique. Thus the set of Huffman codes for a given probability distribution is a non-empty subset of the codes minimizing $L(C)$ for that probability distribution. (However, for each minimizing codeword length assignment, there exists at least one Huffman code with those lengths.)

Basic technique

Compression

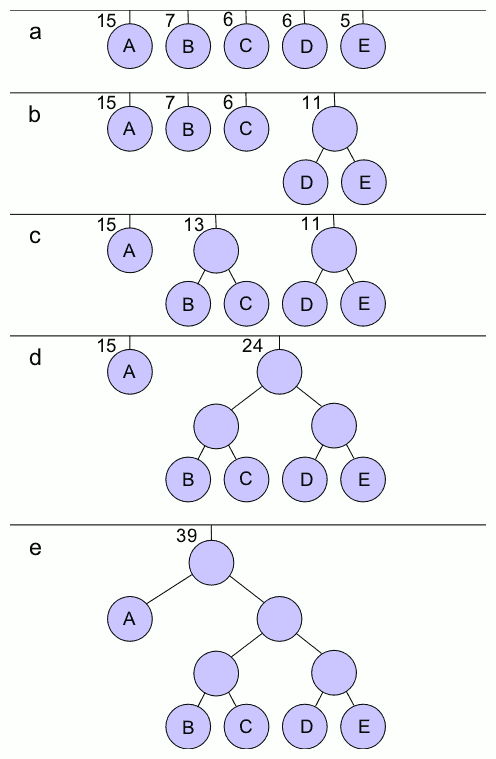
The technique works by creating a binary tree of nodes. These can be stored in a regular array, the size of which depends on the number of symbols, $n$. A node can be either a leaf node or an internal node. Initially, all nodes are leaf nodes, which contain the symbol itself, the weight (frequency of appearance) of the symbol and optionally, a link to a parent node which makes it easy to read the code (in reverse) starting from a leaf node. Internal nodes contain a weight, links to two child nodes and an optional link to a parent node. As a common convention, bit '0' represents following the left child and bit '1' represents following the right child. A finished tree has up to $n$ leaf nodes and $n-1$ internal nodes. A Huffman tree that omits unused symbols produces the most optimal code lengths.

The process begins with the leaf nodes containing the probabilities of the symbol they represent. Then, the process takes the two nodes with smallest probability, and creates a new internal node having these two nodes as children. The weight of the new node is set to the sum of the weight of the children. We then apply the process again, on the new internal node and on the remaining nodes (i.e., we exclude the two leaf nodes), we repeat this process until only one node remains, which is the root of the Huffman tree.

The simplest construction algorithm uses a priority queue where the node with lowest probability is given highest priority:

# Create a leaf node for each symbol and add it to the priority queue.
# While there is more than one node in the queue:
## Remove the two nodes of highest priority (lowest probability) from the queue
## Create a new internal node with these two nodes as children and with probability equal to the sum of the two nodes' probabilities.
## Add the new node to the queue.
# The remaining node is the root node and the tree is complete.

Since efficient priority queue data structures require O(log ''n'') time per insertion, and a tree with ''n'' leaves has 2''n''−1 nodes, this algorithm operates in O(''n'' log ''n'') time, where ''n'' is the number of symbols.

If the symbols are sorted by probability, there is a linear-time (O(''n'')) method to create a Huffman tree using two queues, the first one containing the initial weights (along with pointers to the associated leaves), and combined weights (along with pointers to the trees) being put in the back of the second queue. This assures that the lowest weight is always kept at the front of one of the two queues:

#Start with as many leaves as there are symbols.
#Enqueue all leaf nodes into the first queue (by probability in increasing order so that the least likely item is in the head of the queue).
#While there is more than one node in the queues:
##Dequeue the two nodes with the lowest weight by examining the fronts of both queues.
##Create a new internal node, with the two just-removed nodes as children (either node can be either child) and the sum of their weights as the new weight.
##Enqueue the new node into the rear of the second queue.
#The remaining node is the root node; the tree has now been generated.

Once the Huffman tree has been generated, it is traversed to generate a dictionary which maps the symbols to binary codes as follows:

#Start with current node set to the root.
#If node is not a leaf node, label the edge to the left child as ''0'' and the edge to the right child as ''1''. Repeat the process at both the left child and the right child.

The final encoding of any symbol is then read by a concatenation of the labels on the edges along the path from the root node to the symbol.

In many cases, time complexity is not very important in the choice of algorithm here, since ''n'' here is the number of symbols in the alphabet, which is typically a very small number (compared to the length of the message to be encoded); whereas complexity analysis concerns the behavior when ''n'' grows to be very large.

It is generally beneficial to minimize the variance of codeword length. For example, a communication buffer receiving Huffman-encoded data may need to be larger to deal with especially long symbols if the tree is especially unbalanced. To minimize variance, simply break ties between queues by choosing the item in the first queue. This modification will retain the mathematical optimality of the Huffman coding while both minimizing variance and minimizing the length of the longest character code.

Decompression

Generally speaking, the process of decompression is simply a matter of translating the stream of prefix codes to individual byte values, usually by traversing the Huffman tree node by node as each bit is read from the input stream (reaching a leaf node necessarily terminates the search for that particular byte value). Before this can take place, however, the Huffman tree must be somehow reconstructed. In the simplest case, where character frequencies are fairly predictable, the tree can be preconstructed (and even statistically adjusted on each compression cycle) and thus reused every time, at the expense of at least some measure of compression efficiency. Otherwise, the information to reconstruct the tree must be sent a priori. A naive approach might be to prepend the frequency count of each character to the compression stream. Unfortunately, the overhead in such a case could amount to several kilobytes, so this method has little practical use. If the data is compressed using