Universal Cover

A covering of a topological space $X$ is a continuous map $\pi : E \rightarrow X$ with special properties.

Definition

Let $X$ be a topological space. A covering of $X$ is a continuous map

: $\pi : E \rightarrow X$

such that there exists a discrete space $D$ and for every $x \in X$ an open neighborhood $U \subset X$, such that $\pi^(U)= \displaystyle \bigsqcup_ V_d$ and $\pi, _:V_d \rightarrow U$ is a homeomorphism for every $d \in D$.
Often, the notion of a covering is used for the covering space $E$ as well as for the map $\pi : E \rightarrow X$. The open sets $V_$ are called sheets, which are uniquely determined up to a homeomorphism if $U$ is connected. For each $x \in X$ the discrete subset $\pi^(x)$ is called the fiber of $x$. The degree of a covering is the cardinality of the space $D$. If $E$ is path-connected, then the covering $\pi : E \rightarrow X$ is denoted as a path-connected covering.

Examples

* For every topological space $X$ there exists the covering $\pi:X \rightarrow X$ with $\pi(x)=x$, which is denoted as the trivial covering of $X.$

* The map $r \colon \mathbb \to S^1$ with $r(t)=(\cos(2 \pi t), \sin(2 \pi t))$ is a covering of the unit circle $S^1$. The base of the covering is $S^1$ and the covering space is $\mathbb$. For any point $x = (x_1, x_2) \in S^1$ such that $x_1 > 0$, the set $U := \$ is an open neighborhood of $x$. The preimage of $U$ under $r$ is
::$r^(U)=\displaystyle\bigsqcup_ \left( n - \frac 1 4, n + \frac 1 4\right)$
:and the sheets of the covering are $V_n = (n - 1/4, n+1/4)$ for $n \in \mathbb.$ The fiber of $x$ is
::$r^(x) = \.$

* Another covering of the unit circle is the map $q \colon S^1 \to S^1$ with $q(z)=z^$ for some $n \in \mathbb.$ For an open neighborhood $U$ of an $x \in S^1$, one has:
::$q^(U)=\displaystyle\bigsqcup_^ U$.
* A map which is a local homeomorphism but not a covering of the unit circle is $p \colon \mathbb \to S^1$ with $p(t)=(\cos(2 \pi t), \sin(2 \pi t))$. There is a sheet of an open neighborhood of $(1,0)$, which is not mapped homeomorphically onto $U$.

Properties

Local homeomorphism

Since a covering $\pi:E \rightarrow X$ maps each of the disjoint open sets of $\pi^(U)$ homeomorphically onto $U$ it is a local homeomorphism, i.e. $\pi$ is a continuous map and for every $e \in E$ there exists an open neighborhood $V \subset E$ of $e$, such that $\pi, _V : V \rightarrow \pi(V)$ is a homeomorphism.

It follows that the covering space $E$ and the base space $X$ locally share the same properties.

* If $X$ is a connected and non-orientable manifold, then there is a covering $\pi:\tilde X \rightarrow X$ of degree $2$, whereby $\tilde X$ is a connected and orientable manifold.
* If $X$ is a connected Lie group, then there is a covering $\pi:\tilde X \rightarrow X$ which is also a Lie group homomorphism and $\tilde X := \$ is a Lie group.
* If $X$ is a graph, then it follows for a covering $\pi:E \rightarrow X$ that $E$ is also a graph.
* If $X$ is a connected manifold, then there is a covering $\pi:\tilde X \rightarrow X$, whereby $\tilde X$ is a connected and simply connected manifold.
* If $X$ is a connected Riemann surface, then there is a covering $\pi:\tilde X \rightarrow X$ which is also a holomorphic map and $\tilde X$ is a connected and simply connected Riemann surface.

Factorisation

Let $p,q$ and $r$ be continuous maps, such that the diagram

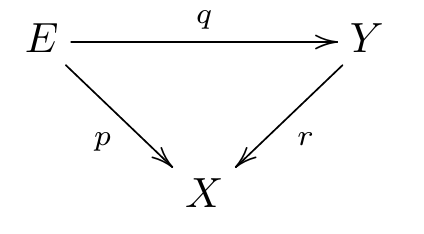
commutes.

* If $p$ and $q$ are coverings, so is $r$.
* If $p$ and $r$ are coverings, so is $q$.

Product of coverings

Let $X$ and $X'$ be topological spaces and $p:E \rightarrow X$ and $p':E' \rightarrow X'$ be coverings, then $p \times p':E \times E' \rightarrow X \times X'$ with $(p \times p')(e, e') = (p(e), p'(e'))$ is a covering.

Equivalence of coverings

Let $X$ be a topological space and $p:E \rightarrow X$ and $p':E' \rightarrow X$ be coverings. Both coverings are called equivalent, if there exists a homeomorphism $h:E \rightarrow E'$, such that the diagram

commutes. If such a homeomorphism exists, then one calls the covering spaces $E$ and $E'$ isomorphic.

Lifting property

An important property of the covering is, that it satisfies the lifting property, i.e.:

Let $I$ be the unit interval and $p:E \rightarrow X$ be a covering. Let $F:Y \times I \rightarrow X$ be a continuous map and $\tilde F_0:Y \times \ \rightarrow E$ be a lift of $F, _$, i.e. a continuous map such that $p \circ \tilde F_0 = F, _$. Then there is a uniquely determined, continuous map $\tilde F:Y \times I \rightarrow E$, which is a lift of $F$, i.e. $p \circ \tilde F = F$.

If $X$ is a path-connected space, then for $Y=\$ it follows that the map $\tilde F$ is a lift of a path in $X$ and for $Y=I$ it is a lift of a homotopy of paths in $X$.

Because of that property one can show, that the fundamental group $\pi_(S^1)$ of the unit circle is an infinite cyclic group, which is generated by the homotopy classes of the loop $\gamma: I \rightarrow S^1$ with $\gamma (t) = (\cos(2 \pi t), \sin(2 \pi t))$.

Let $X$ be a path-connected space and $p:E \rightarrow X$ be a connected covering. Let $x,y \in X$ be any two points, which are connected by a path $\gamma$, i.e. $\gamma(0)= x$ and $\gamma(1)= y$. Let $\tilde \gamma$ be the unique lift of $\gamma$, then the map

: $L_:p^(x) \rightarrow p^(y)$ with $L_(\tilde \gamma (0))=\tilde \gamma (1)$

is bijective.

If $X$ is a path-connected space and $p: E \rightarrow X$ a connected covering, then the induced group homomorphism

: $p_: \pi_(E) \rightarrow \pi_(X)$ with p_( gamma= \circ \gamma/math>,

is injective and the subgroup $p_(\pi_1(E))$ of $\pi_1(X)$ consists of the homotopy classes of loops in $X$, whose lifts are loops in $E$.

Branched covering

Definitions

Holomorphic maps between Riemann surfaces

Let $X$ and $Y$ be Riemann surfaces, i.e. one dimensional complex manifolds, and let $f: X \rightarrow Y$ be a continuous map. $f$ is holomorphic in a point $x \in X$, if for any charts $\phi _x:U_1 \rightarrow V_1$ of $x$ and $\phi_:U_2 \rightarrow V_2$ of $f(x)$, with $\phi_x(U_1) \subset U_2$, the map $\phi _ \circ f \circ \phi^ _x: \mathbb \rightarrow \mathbb$ is holomorphic.

If $f$ is holomorphic at all $x \in X$, we say $f$ is holomorphic.

The map $F =\phi _ \circ f \circ \phi^ _x$ is called the local expression of $f$ in $x \in X$.

If $f: X \rightarrow Y$ is a non-constant, holomorphic map between compact Riemann surfaces, then $f$ is surjective and an open map, i.e. for every open set $U \subset X$ the image $f(U) \subset Y$ is also open.

Ramification point and branch point

Let $f: X \rightarrow Y$ be a non-constant, holomorphic map between compact Riemann surfaces. For every $x \in X$ there exist charts for $x$ and $f(x)$ and there exists a uniquely determined $k_x \in \mathbb$, such that the local expression $F$ of $f$ in $x$ is of the form $z \mapsto z^$. The number $k_x$ is called the ramification index of $f$ in $x$ and the point $x \in X$ is called a ramification point if $k_x \geq 2$. If $k_x =1$ for an $x \in X$, then $x$ is unramified. The image point $y=f(x) \in Y$ of a ramification point is called a branch point.

Degree of a holomorphic map

Let $f: X \rightarrow Y$ be a non-constant, holomorphic map between compact Riemann surfaces. The degree $\operatorname(f)$ of $f$ is the cardinality of the fiber of an unramified point $y=f(x) \in Y$, i.e. $\operatorname(f):=, f^(y),$.

This number is well-defined, since for every $y \in Y$ the fiber $f^(y)$ is discrete and for any two unramified points $y_1,y_2 \in Y$, it is: $, f^(y_1), =, f^(y_2), .$

It can be calculated by:

: $\sum_ k_x = \operatorname(f)$

Branched covering

Definition

A continuous map $f: X \rightarrow Y$ is called a branched covering, if there exists a closed set with dense complement $E \subset Y$, such that $f_:X \smallsetminus f^(E) \rightarrow Y \smallsetminus E$ is a covering.

Examples

* Let $n \in \mathbb$ and $n \geq 2$, then $f:\mathbb \rightarrow \mathbb$ with $f(z)=z^n$ is branched covering of degree $n$, whereby $z=0$ is a branch point.
* Every non-constant, holomorphic map between compact Riemann surfaces $f: X \rightarrow Y$ of degree $d$ is a branched covering of degree $d$.

Universal covering

Definition

Let $p: \tilde X \rightarrow X$ be a simply connected covering. If $\beta : E \rightarrow X$ is another simply connected covering, then there exists a uniquely determined homeomorphism $\alpha : \tilde X \rightarrow E$, such that the diagram

commutes.

This means that $p$ is, up to equivalence, uniquely determined and because of that universal property denoted as the universal covering of the space $X$.

Existence

A universal covering does not always exist, but the following properties guarantee its existence:

Let $X$ be a connected, locally simply connected topological space; then, there exists a universal covering $p:\tilde X \rightarrow X$.

$\tilde X$ is defined as $\tilde X := \/\text$ and $p:\tilde X \rightarrow X$ by p( gamma:=\gamma(1).

The topology on $\tilde X$ is constructed as follows: Let $\gamma:I \rightarrow X$ be a path with $\gamma(0)=x_0$. Let $U$ be a simply connected neighborhood of the endpoint $x=\gamma(1)$, then for every $y \in U$ the paths $\sigma_y$ inside $U$ from $x$ to $y$ are uniquely determined up to homotopy. Now consider $\tilde U:=\/\text$, then $p_: \tilde U \rightarrow U$ with p( gamma.\sigma_y=\gamma.\sigma_y(1)=y is a bijection and $\tilde U$ can be equipped with the final topology of $p_$.

The fundamental group $\pi_(X,x_0) = \Gamma$ acts freely through ( gamma tilde x \mapsto gamma.\tilde x/math> on $\tilde X$ and $\psi:\Gamma \backslash \tilde X \rightarrow X$ with \psi( Gamma \tilde x=\tilde x(1) is a homeomorphism, i.e. $\Gamma \backslash \tilde X \cong X$.

Examples

* $r \colon \mathbb \to S^1$ with $r(t)=(\cos(2 \pi t), \sin(2 \pi t))$ is the universal covering of the unit circle $S^1$.
* $p \colon S^n \to \mathbbP^n \cong \\backslash S^n$ with p(x)= /math> is the universal covering of the projective space $\mathbbP^n$ for $n>1$.
* $q \colon SU(n) \ltimes \mathbb \to U(n)$ with $q(A,t)= \begin \exp(2 \pi i t) & 0\\ 0 & I_ \end_\vphantom A$ is the universal covering of the unitary group $U(n)$.
* Since $SU(2) \cong S^3$, it follows that the quotient map $f:SU(2) \rightarrow \mathbb \backslash SU(2) \cong SO(3)$ is the universal covering of the $SO(3)$.
* A topological space which has no universal covering is the Hawaiian earring: $X = \bigcup_\left\$ One can show that no neighborhood of the origin $(0,0)$ is simply connected.

Deck transformation

Definition

Let $p:E \rightarrow X$ be a covering. A deck transformation is a homeomorphism $d:E \rightarrow E$, such that the diagram of continuous maps

commutes. Together with the composition of maps, the set of deck transformation forms a group $\operatorname(p)$, which is the same as $\operatorname(p)$.

Examples

* Let $q \colon S^1 \to S^1$ be the covering $q(z)=z^$ for some $n \in \mathbb$, then the map $d:S^1 \rightarrow S^1 : z \mapsto z \, e^$ is a deck transformation and $\operatorname(q)\cong \mathbb/ \mathbb$.
* Let $r \colon \mathbb \to S^1$ be the covering $r(t)=(\cos(2 \pi t), \sin(2 \pi t))$, then the map $d_k:\mathbb \rightarrow \mathbb : t \mapsto t + k$ with $k \in \mathbb$ is a deck transformation and $\operatorname(r)\cong \mathbb$.

Properties

Let $X$ be a path-connected space and $p:E \rightarrow X$ be a connected covering. Since a deck transformation $d:E \rightarrow E$ is bijective, it permutes the elements of a fiber $p^(x)$ with $x \in X$ and is uniquely determined by where it sends a single point. In particular, only the identity map fixes a point in the fiber. Because of this property every deck transformation defines a group action on $E$, i.e. let $U \subset X$ be an open neighborhood of a $x \in X$ and $\tilde U \subset E$ an open neighborhood of an $e \in p^(x)$, then $\operatorname(p) \times E \rightarrow E: (d,\tilde U)\mapsto d(\tilde U)$ is a group action.

Normal coverings

Definition

A covering $p:E \rightarrow X$ is called normal, if $\operatorname(p) \backslash E \cong X$. This means, that for every $x \in X$ and any two $e_0,e_1 \in p^(x)$ there exists a deck transformation $d:E \rightarrow E$, such that $d(e_0)=e_1$.

Properties

Let $X$ be a path-connected space and $p:E \rightarrow X$ be a connected covering. Let $H=p_(\pi_1(E))$ be a subgroup of $\pi_1(X)$, then $p$ is a normal covering iff $H$ is a normal subgroup of $\pi_1(X)$.

If $p:E \rightarrow X$ is a normal covering and $H=p_(\pi_1(E))$, then $\operatorname(p) \cong \pi_1(X)/H$.

If $p:E \rightarrow X$ is a path-connected covering and $H=p_(\pi_1(E))$, then $\operatorname(p) \cong N(H)/H$, whereby $N(H)$ is the normaliser of $H$.

Let $E$ be a topological space. A group $\Gamma$ acts discontinuously on $E$, if every $e \in E$ has an open neighborhood $V \subset E$ with $V \neq \empty$, such that for every $\gamma \in \Gamma$ with $\gamma V \cap V \neq \empty$ one has $d_1 = d_2$.

If a group $\Gamma$ acts discontinuously on a topological space $E$, then the quotient map $q: E \rightarrow \Gamma \backslash E$ with $q(e)=\Gamma e$ is a normal covering. Hereby $\Gamma \backslash E = \$ is the quotient space and $\Gamma e = \$ is the orbit of the group action.

Examples

* The covering $q \colon S^1 \to S^1$ with $q(z)=z^$ is a normal coverings for every $n \in \mathbb$.
* Every simply connected covering is a normal covering.

Calculation

Let $\Gamma$ be a group, which acts discontinuously on a topological space $E$ and let $q: E \rightarrow \Gamma \backslash E$ be the normal covering.

* If $E$ is path-connected, then $\operatorname(q) \cong \Gamma$.

* If $E$ is simply connected, then $\operatorname(q)\cong \pi_1(X)$.

Examples

* Let $n \in \mathbb$. The antipodal map $g:S^n \rightarrow S^n$ with $g(x)=-x$ generates, together with the composition of maps, a group $D(g) \cong \mathbb$ and induces a group action $D(g) \times S^n \rightarrow S^n, (g,x)\mapsto g(x)$, which acts discontinuously on $S^n$. Because of $\mathbb \backslash S^n \cong \mathbbP^n$ it follows, that the quotient map $q \colon S^n \rightarrow \mathbb\backslash S^n \cong \mathbbP^n$ is a normal covering and for $n > 1$ a universal covering, hence $\operatorname(q)\cong \mathbb\cong \pi_1()$ for $n > 1$.
* Let $SO(3)$ be the special orthogonal group, then the map $f:SU(2) \rightarrow SO(3) \cong \mathbb \backslash SU(2)$ is a normal covering and because of $SU(2) \cong S^3$, it is the universal covering, hence $\operatorname(f) \cong \mathbb \cong \pi_1(SO(3))$.
* With the group action $(z_1,z_2)*(x,y)=(z_1+(-1)^x,z_2+y)$ of $\mathbb$ on $\mathbb$, whereby $(\mathbb,*)$ is the semidirect product $\mathbb \rtimes \mathbb$, one gets the universal covering $f: \mathbb \rightarrow (\mathbb \rtimes \mathbb) \backslash \mathbb \cong K$ of the klein bottle $K$, hence $\operatorname(f) \cong \mathbb \rtimes \mathbb \cong \pi_1(K)$.
* Let $T = S^1 \times S^1$ be the torus which is embedded in the $\mathbb$. Then one gets a homeomorphism $\alpha: T \rightarrow T: (e^,e^) \mapsto (e^,e^)$, which induces a discontinuous group action $G_ \times T \rightarrow T$, whereby $G_ \cong \mathbb$. It follows, that the map $f: T \rightarrow G_ \backslash T \cong K$ is a normal covering of the klein bottle, hence $\operatorname(f) \cong \mathbb$.
* Let $S^3$ be embedded in the $\mathbb$. Since the group action S^3 \times \mathbb \rightarrow S^3: ((z_1,z_2), \mapsto (e^z_1,e^z_2) is discontinuously, whereby $p,q \in \mathbb$ are coprime, the map $f:S^3 \rightarrow \mathbb \backslash S^3 =: L_$ is the universal covering of the lens space $L_$, hence $\operatorname(f) \cong \mathbb \cong \pi_1(L_)$.

Galois correspondence

Let $X$ be a connected and locally simply connected space, then for every subgroup $H\subseteq \pi_1(X)$ there exists a path-connected covering $\alpha:X_H \rightarrow X$ with $\alpha_(\pi_1(X_H))=H$.

Let $p_1:E \rightarrow X$ and $p_2: E' \rightarrow X$ be two path-connected coverings, then they are equivalent iff the subgroups $H = p_(\pi_1(E))$ and $H'=p_(\pi_1(E'))$ are conjugate to each other.

Let $X$ be a connected and locally simply connected space, then, up to equivalence between coverings, there is a bijection:

$\begin \qquad \displaystyle \ & \longleftrightarrow & \displaystyle \ \\ H & \longrightarrow & \alpha:X_H \rightarrow X \\ p_\#(\pi_1(E))&\longleftarrow & p \\ \displaystyle \ & \longleftrightarrow & \displaystyle \ \\ H & \longrightarrow & \alpha:X_H \rightarrow X \\ p_\#(\pi_1(E))&\longleftarrow & p \end$

For a sequence of subgroups $\displaystyle \ \subset H \subset G \subset \pi_1(X)$ one gets a sequence of coverings $\tilde X \longrightarrow X_H \cong H \backslash \tilde X \longrightarrow X_G \cong G \backslash \tilde X \longrightarrow X\cong \pi_1(X) \backslash \tilde X$. For a subgroup $H \subset \pi_1(X)$ with index
\displaystyle pi_1(X):H= d
, the covering $\alpha:X_H \rightarrow X$ has degree $d$.

Classification

Definitions

Category of coverings

Let $X$ be a topological space. The objects of the category $\boldsymbol$ are the coverings $p:E \rightarrow X$ of $X$ and the morphisms between two coverings $p:E \rightarrow X$ and $q:F\rightarrow X$ are continuous maps $f:E \rightarrow F$, such that the diagram

commutes.

G-Set

Let $G$ be a topological group. The category $\boldsymbol$ is the category of sets which are G-sets. The morphisms are G-maps $\phi:X \rightarrow Y$ between G-sets. They satisfy the condition $\phi(gx)=g \, \phi(x)$ for every $g \in G$.

Equivalence

Let $X$ be a connected and locally simply connected space, $x \in X$ and $G = \pi_1(X,x)$ be the fundamental group of $X$. Since $G$ defines, by lifting of paths and evaluating at the endpoint of the lift, a group action on the fiber of a covering, the functor $F:\boldsymbol \longrightarrow \boldsymbol: p \mapsto p^(x)$ is an equivalence of categories.

Applications

An important practical application of covering spaces occurs in charts on SO(3), the rotation group. This group occurs widely in engineering, due to 3-dimensional rotations being heavily used in navigation, nautical engineering, and aerospace engineering, among many other uses. Topologically, SO(3) is the real projective space RP³, with fundamental group Z/2, and only (non-trivial) covering space the hypersphere ''S''³, which is the group Spin(3), and represented by the unit quaternions. Thus quaternions are a preferred method for representing spatial rotations – see quaternions and spatial rotation.

However, it is often desirable to represent rotations by a set of three numbers, known as Euler angles (in numerous variants), both because this is conceptually simpler for someone familiar with planar rotation, and because one can build a combination of three gimbals to produce rotations in three dimensions. Topologically this corresponds to a map from the 3-torus ''T''³ of three angles to the real projective space RP³ of rotations, and the resulting map has imperfections due to this map being unable to be a covering map. Specifically, the failure of the map to be a local homeomorphism at certain points is referred to as gimbal lock, and is demonstrated in the animation at the right – at some points (when the axes are coplanar) the rank of the map is 2, rather than 3, meaning that only 2 dimensions of rotations can be realized from that point by changing the angles. This causes problems in applications, and is formalized by the notion of a covering space.

See also

* Bethe lattice is the universal cover of a Cayley graph
* Covering graph, a covering space for an undirected graph, and its special case the bipartite double cover
* Covering group
*Galois connection
* Quotient space (topology)

Literature

* Allen Hatcher: ''Algebraic Topology''. Cambridge Univ. Press, Cambridge, ISBN 0-521-79160-X
* Otto Forster: ''Lectures on Riemann surfaces''. Springer Berlin, München 1991, ISBN 978-3-540-90617-9
* James Munkres: ''Topology''. Upper Saddle River, NJ: Prentice Hall, Inc., ©2000, ISBN 978-0-13-468951-7
* Wolfgang Kühnel: ''Matrizen und Lie-Gruppen''. Springer Fachmedien Wiesbaden GmbH, Stuttgart, ISBN 978-3-8348-9905-7

References

Algebraic topology
Homotopy theory
Fiber bundles
Topological graph theory