|
Klein Bottle
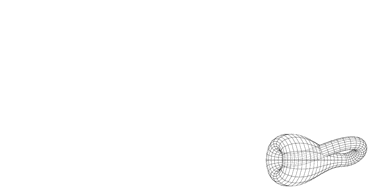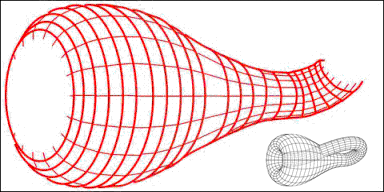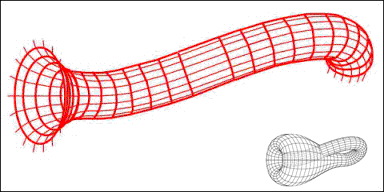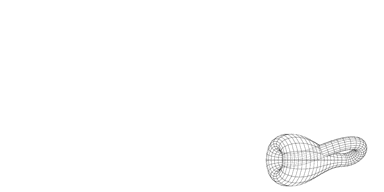
In mathematics, the Klein bottle () is an example of a Orientability, non-orientable Surface (topology), surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. More formally, the Klein bottle is a two-dimensional manifold on which one cannot define a normal vector at each point that varies continuous function, continuously over the whole manifold. Other related non-orientable surfaces include the Möbius strip and the real projective plane. While a Möbius strip is a surface with a Boundary (topology), boundary, a Klein bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary. The Klein bottle was first described in 1882 by the mathematician Felix Klein. Construction The following square is a fundamental polygon of the Klein bottle. The idea is to 'glue' together the corresponding red and blue edges with the arrows matching, as in the diagr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Polygon
In mathematics, a fundamental polygon can be defined for every compact Riemann surface of genus greater than 0. It encodes not only information about the topology of the surface through its fundamental group but also determines the Riemann surface up to conformal equivalence. By the uniformization theorem, every compact Riemann surface has simply connected universal covering surface given by exactly one of the following: *the Riemann sphere, *the complex plane, *the unit disk ''D'' or equivalently the upper half-plane ''H''. In the first case of genus zero, the surface is conformally equivalent to the Riemann sphere. In the second case of genus one, the surface is conformally equivalent to a torus C/Λ for some lattice Λ in C. The fundamental polygon of Λ, if assumed convex, may be taken to be either a period parallelogram or a centrally symmetric hexagon, a result first proved by Fedorov in 1891. In the last case of genus ''g'' > 1, the Riemann surface is conformally equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Klein Bottle
In mathematics, the Klein bottle () is an example of a Orientability, non-orientable Surface (topology), surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. More formally, the Klein bottle is a two-dimensional manifold on which one cannot define a normal vector at each point that varies continuous function, continuously over the whole manifold. Other related non-orientable surfaces include the Möbius strip and the real projective plane. While a Möbius strip is a surface with a Boundary (topology), boundary, a Klein bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary. The Klein bottle was first described in 1882 by the mathematician Felix Klein. Construction The following square is a fundamental polygon of the Klein bottle. The idea is to 'glue' together the corresponding red and blue edges with the arrows matching, as in the diagr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orientability
In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "anticlockwise". A space is orientable if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an orientation of the space. Real vector spaces, Euclidean spaces, and spheres are orientable. A space is non-orientable if "clockwise" is changed into "counterclockwise" after running through some loops in it, and coming back to the starting point. This means that a geometric shape, such as , that moves continuously along such a loop is changed into its own mirror image . A Möbius strip is an example of a non-orientable space. Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds oft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fiber Bundle
In mathematics, and particularly topology, a fiber bundle ( ''Commonwealth English'': fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a product space B \times F is defined using a continuous surjective map, \pi : E \to B, that in small regions of E behaves just like a projection from corresponding regions of B \times F to B. The map \pi, called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space E is known as the total space of the fiber bundle, B as the base space, and F the fiber. In the '' trivial'' case, E is just B \times F, and the map \pi is just the projection from the product space to the first factor. This is called a trivial bundle. Examples of non-trivial fiber bundles include the Möbius strip and Klein bottle, as well as nontrivial covering spaces. Fiber bundles, such as the tangent bundle of a manifol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marc Ten Bosch
is an in-development puzzle-platform video game by Marc ten Bosch set in a world with four spatial dimensions. Because rendering true four-dimensional (4D) space to a screen is impossible, the game renders two-dimensional images (the screen) of three-dimensional (3D) slices of its world. Players can change the dimensions used to create the slice and move within the slice, thereby enabling them to move throughout the 4D world. The game has many puzzles that are impossible to solve in a 3D world, but are solvable in the game's 4D world. In contrast to traditional 2D or 3D game development, virtually all of the technology behind ''Miegakure'' had to be created from scratch because the equations describing physics in a world with four spatial dimensions differ from those in spacetime (which has only three spatial dimensions). The technology underlying the game was used to create the 2017 simulation game ''4D Toys'', and some of the research underlying the game was published at SIGG ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherinder
In Four-dimensional space, four-dimensional geometry, the spherinder, or spherical cylinder or spherical prism, is a geometric object, defined as the Cartesian product of a 3-ball (mathematics), ball (or solid 2-sphere) of radius ''r''1 and a line segment of length 2''r''2: :D = \ Like the duocylinder, it is also analogous to a Cylinder (geometry), cylinder in 3-space, which is the Cartesian product of a disk with a line segment. It is a rotatope and a toratope. It can be seen in 3-dimensional space by stereographic projection as two concentric spheres, in a similar way that a tesseract (cubic prism) can be projected as two concentric cubes, and how a circular cylinder can be projected into 2-dimensional space as two concentric circles. Spherindrical coordinate system One can define a "spherindrical" coordinate system , consisting of spherical coordinates with an extra coordinate . This is analogous to how cylindrical coordinates are defined: and being Polar coordinate syste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' of any positive integer dimension ''n'', which are called Euclidean ''n''-spaces when one wants to specify their dimension. For ''n'' equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called '' postulates'', which either were considered as evid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Space
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces. One suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square (geometry)
In geometry, a square is a regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal sides. As with all rectangles, a square's angles are right angles (90 degrees, or /2 radians), making adjacent sides perpendicular. The area of a square is the side length multiplied by itself, and so in algebra, multiplying a number by itself is called squaring. Equal squares can tile the plane edge-to-edge in the square tiling. Square tilings are ubiquitous in tiled floors and walls, graph paper, image pixels, and game boards. Square shapes are also often seen in building floor plans, origami paper, food servings, in graphic design and heraldry, and in instant photos and fine art. The formula for the area of a square forms the basis of the calculation of area and motivates the search for methods for squaring the circle by compass and straightedge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quotient Space (topology)
In topology and related areas of mathematics, the quotient space of a topological space under a given equivalence relation is a new topological space constructed by endowing the quotient set of the original topological space with the quotient topology, that is, with the finest topology that makes continuous the canonical projection map (the function that maps points to their equivalence classes). In other words, a subset of a quotient space is open if and only if its preimage under the canonical projection map is open in the original topological space. Intuitively speaking, the points of each equivalence class are or "glued together" for forming a new topological space. For example, identifying the points of a sphere that belong to the same diameter produces the projective plane as a quotient space. Definition Let X be a topological space, and let \sim be an equivalence relation on X. The quotient set Y = X/ is the set of equivalence classes of elements of X. The e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cheshire Cat
The Cheshire Cat ( ) is a fictional cat popularised by Lewis Carroll in ''Alice's Adventures in Wonderland'' and known for its distinctive mischievous grin. While now most often used in ''Alice''-related contexts, the association of a "Cheshire cat" with grinning predates the 1865 book. It has transcended the context of literature and become enmeshed in popular culture, appearing in various forms of media, from political cartoons to television, as well as in cross-disciplinary studies, from business to science. Often it is shown in the context of a person or idea that is purposefully confusing or enigmatic. One distinguishing feature of the ''Alice''-style Cheshire Cat is the periodic gradual disappearance of its body, leaving only one last visible trace: its iconic grin. He belongs to the Duchess. Origins The first known appearance of the expression in literature is in the 18th century, in Francis Grose's ''A Classical Dictionary of the Vulgar Tongue'', Second, Correct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |