Tensor (machine Learning) on:
[Wikipedia]
[Google]
[Amazon]
In
 Another approach to using tensors in machine learning is to embed various data types directly. For example, a
Another approach to using tensors in machine learning is to embed various data types directly. For example, a
 Tensors may be used as the unit values of neural networks which extend the concept of scalar, vector and matrix values to multiple dimensions.
The output value of single layer unit is the sum-product of its input units and the connection weights filtered through the
Tensors may be used as the unit values of neural networks which extend the concept of scalar, vector and matrix values to multiple dimensions.
The output value of single layer unit is the sum-product of its input units and the connection weights filtered through the 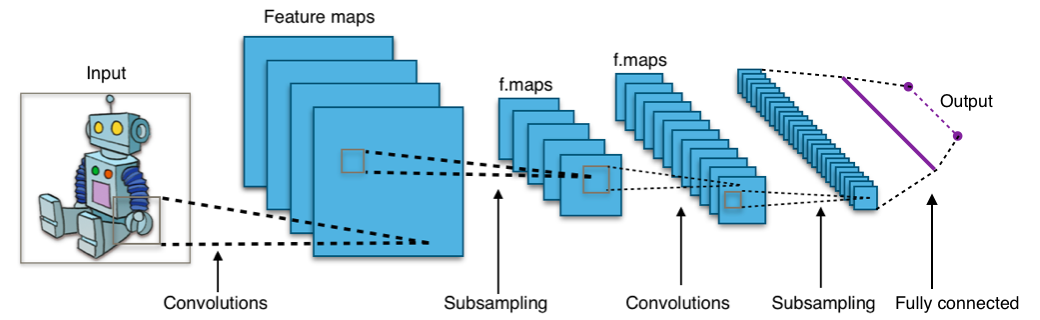 If each output element of is a scalar, then we have the classical definition of an
If each output element of is a scalar, then we have the classical definition of an

cuDNN
CUDA Deep Neural Network, a library for a set of optimized primitives written in the parallel CUDA language. CUDA and thus cuDNN run on dedicated GPUs that implement unified massive parallelism in hardware. These GPUs were not yet dedicated chips for tensors, but rather existing hardware adapted for parallel computation in machine learning. In the period 2015–2017
machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
, the term tensor informally refers to two different concepts (i) a way of organizing data and (ii) a multilinear (tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
) transformation. Data may be organized in a multidimensional array
In computer science, array is a data type that represents a collection of ''elements'' (values or variables), each selected by one or more indices (identifying keys) that can be computed at run time during program execution. Such a collection i ...
(''M''-way array), informally referred to as a "data tensor"; however, in the strict mathematical sense, a tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
is a multilinear mapping over a set of domain vector spaces to a range vector space. Observations, such as images, movies, volumes, sounds, and relationships among words and concepts, stored in an ''M''-way array ("data tensor"), may be analyzed either by artificial neural networks
In machine learning, a neural network (also artificial neural network or neural net, abbreviated ANN or NN) is a computational model inspired by the structure and functions of biological neural networks.
A neural network consists of connected ...
or tensor methods.
Tensor decomposition
In multilinear algebra, a tensor decomposition is any scheme for expressing a "data tensor" (M-way array) as a sequence of elementary operations acting on other, often simpler tensors. Many tensor decompositions generalize some matrix decomposi ...
factorizes data tensors into smaller tensors. Operations on data tensors can be expressed in terms of matrix multiplication
In mathematics, specifically in linear algebra, matrix multiplication is a binary operation that produces a matrix (mathematics), matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the n ...
and the Kronecker product
In mathematics, the Kronecker product, sometimes denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a specialization of the tensor product (which is denoted by the same symbol) from vector ...
. The computation of gradients, a crucial aspect of backpropagation
In machine learning, backpropagation is a gradient computation method commonly used for training a neural network to compute its parameter updates.
It is an efficient application of the chain rule to neural networks. Backpropagation computes th ...
, can be performed using software libraries
In computing, a library is a collection of resources that can be leveraged during software development to implement a computer program. Commonly, a library consists of executable code such as compiled functions and classes, or a library can ...
such as PyTorch
PyTorch is a machine learning library based on the Torch library, used for applications such as computer vision and natural language processing, originally developed by Meta AI and now part of the Linux Foundation umbrella. It is one of the mo ...
and TensorFlow
TensorFlow is a Library (computing), software library for machine learning and artificial intelligence. It can be used across a range of tasks, but is used mainly for Types of artificial neural networks#Training, training and Statistical infer ...
.
Computations are often performed on graphics processing unit
A graphics processing unit (GPU) is a specialized electronic circuit designed for digital image processing and to accelerate computer graphics, being present either as a discrete video card or embedded on motherboards, mobile phones, personal ...
s (GPUs) using CUDA
In computing, CUDA (Compute Unified Device Architecture) is a proprietary parallel computing platform and application programming interface (API) that allows software to use certain types of graphics processing units (GPUs) for accelerated gene ...
, and on dedicated hardware such as Google
Google LLC (, ) is an American multinational corporation and technology company focusing on online advertising, search engine technology, cloud computing, computer software, quantum computing, e-commerce, consumer electronics, and artificial ...
's Tensor Processing Unit or Nvidia
Nvidia Corporation ( ) is an American multinational corporation and technology company headquartered in Santa Clara, California, and incorporated in Delaware. Founded in 1993 by Jensen Huang (president and CEO), Chris Malachowsky, and Curti ...
's Tensor core. These developments have greatly accelerated neural network architectures, and increased the size and complexity of models that can be trained.
History
Atensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
is by definition a multilinear map. In mathematics, this may express a multilinear relationship between sets of algebraic objects. In physics, tensor fields
In mathematics and physics, a tensor field is a function assigning a tensor to each point of a region of a mathematical space (typically a Euclidean space or manifold) or of the physical space. Tensor fields are used in differential geometry, a ...
, considered as tensors at each point in space, are useful in expressing mechanics such as stress or elasticity. In machine learning, the exact use of tensors depends on the statistical approach being used.
In 2001, the field of signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomograph ...
and statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
were making use of tensor methods. Pierre Comon surveys the early adoption of tensor methods in the fields of telecommunications, radio surveillance, chemometrics and sensor processing. Linear tensor rank methods (such as, Parafac/CANDECOMP) analyzed M-way arrays ("data tensors") composed of higher order statistics that were employed in blind source separation problems to compute a linear model of the data. He noted several early limitations in determining the tensor rank and efficient tensor rank decomposition.
In the early 2000s, multilinear tensor methods crossed over into computer vision, computer graphics and machine learning with papers by Vasilescu or in collaboration with Terzopoulos, such as Human Motion Signatures, TensorFaces TensorTexures and Multilinear Projection. Multilinear algebra, the algebra of higher-order tensors, is a suitable and transparent framework for analyzing the multifactor structure of an ensemble of observations and for addressing the difficult problem of disentangling the causal factors based on second order or higher order statistics associated with each causal factor.
Tensor (multilinear) factor analysis disentangles and reduces the influence of different causal factors with multilinear subspace learning.
When treating an image or a video as a 2- or 3-way array, i.e., "data matrix/tensor", tensor methods reduce spatial or time redundancies as demonstrated by Wang and Ahuja.
Yoshua Bengio,
Geoff Hinton
and their collaborators briefly discuss the relationship between deep neural networks and tensor factor analysis beyond the use of M-way arrays ("data tensors") as inputs. One of the early uses of tensors for neural networks
A neural network is a group of interconnected units called neurons that send signals to one another. Neurons can be either Cell (biology), biological cells or signal pathways. While individual neurons are simple, many of them together in a netwo ...
appeared in natural language processing
Natural language processing (NLP) is a subfield of computer science and especially artificial intelligence. It is primarily concerned with providing computers with the ability to process data encoded in natural language and is thus closely related ...
. A single word can be expressed as a vector via Word2vec
Word2vec is a technique in natural language processing (NLP) for obtaining vector representations of words. These vectors capture information about the meaning of the word based on the surrounding words. The word2vec algorithm estimates these rep ...
. Thus a relationship between two words can be encoded in a matrix. However, for more complex relationships such as subject-object-verb, it is necessary to build higher-dimensional networks. In 2009, the work of Sutskever introduced Bayesian Clustered Tensor Factorization to model relational concepts while reducing the parameter space. From 2014 to 2015, tensor methods become more common in convolutional neural networks
A convolutional neural network (CNN) is a type of feedforward neural network that learns features via filter (or kernel) optimization. This type of deep learning network has been applied to process and make predictions from many different type ...
(CNNs). Tensor methods organize neural network weights in a "data tensor", analyze and reduce the number of neural network weights. Lebedev et al. accelerated CNN networks for character classification (the recognition of letters and digits in images) by using 4D kernel tensors.
Definition
Let be afield
Field may refer to:
Expanses of open ground
* Field (agriculture), an area of land used for agricultural purposes
* Airfield, an aerodrome that lacks the infrastructure of an airport
* Battlefield
* Lawn, an area of mowed grass
* Meadow, a grass ...
such as the real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
s or the complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s . A tensor is a multilinear transformation from a set of domain vector spaces to a range vector space:
Here, and are positive integers, and is the number of ''modes'' of a tensor (also known as the number of ways of a multi-way array). The dimensionality of mode is , for .
In statistics and machine learning, an image is vectorized when viewed as a single observation, and a collection of vectorized images is organized as a "data tensor". For example, a set of facial images with pixels that are the consequences of multiple causal factors, such as a facial geometry , an expression , an illumination condition , and a viewing condition may be organized into a data tensor (ie. multiway array) where are the total number of facial geometries, are the total number of expressions, are the total number of illumination conditions, and are the total number of viewing conditions. Tensor factorizations methods such as TensorFaces and multilinear (tensor) independent component analysis factorizes the data tensor into a set of vector spaces that span the causal factor representations, where an image is the result of tensor transformation that maps a set of causal factor representations to the pixel space.
 Another approach to using tensors in machine learning is to embed various data types directly. For example, a
Another approach to using tensors in machine learning is to embed various data types directly. For example, a grayscale image
In digital photography, computer-generated imagery, and colorimetry, a greyscale (more common in Commonwealth English) or grayscale (more common in American English) image is one in which the value of each pixel is a single sample (signal), s ...
, commonly represented as a discrete 2-way array with dimensionality where are the number of rows and are the number of columns. When an image is treated as 2-way array or 2nd order tensor (i.e. as a collection of column/row observations), tensor factorization methods compute the image column space, the image row space and the normalized PCA coefficients or the ICA coefficients.
Similarly, a color image with RGB channels, may be viewed as a 3rd order data tensor or 3-way array.--------
In natural language processing, a word might be expressed as a vector via the Word2vec
Word2vec is a technique in natural language processing (NLP) for obtaining vector representations of words. These vectors capture information about the meaning of the word based on the surrounding words. The word2vec algorithm estimates these rep ...
algorithm. Thus becomes a mode-1 tensor
:
The embedding of subject-object-verb semantics requires embedding relationships among three words. Because a word is itself a vector, subject-object-verb semantics could be expressed using mode-3 tensors
:
In practice the neural network designer is primarily concerned with the specification of embeddings, the connection of tensor layers, and the operations performed on them in a network. Modern machine learning frameworks manage the optimization, tensor factorization and backpropagation automatically.
As unit values
 Tensors may be used as the unit values of neural networks which extend the concept of scalar, vector and matrix values to multiple dimensions.
The output value of single layer unit is the sum-product of its input units and the connection weights filtered through the
Tensors may be used as the unit values of neural networks which extend the concept of scalar, vector and matrix values to multiple dimensions.
The output value of single layer unit is the sum-product of its input units and the connection weights filtered through the activation function
The activation function of a node in an artificial neural network is a function that calculates the output of the node based on its individual inputs and their weights. Nontrivial problems can be solved using only a few nodes if the activation f ...
:
:
where
:
 If each output element of is a scalar, then we have the classical definition of an
If each output element of is a scalar, then we have the classical definition of an artificial neural network
In machine learning, a neural network (also artificial neural network or neural net, abbreviated ANN or NN) is a computational model inspired by the structure and functions of biological neural networks.
A neural network consists of connected ...
. By replacing each unit component with a tensor, the network is able to express higher dimensional data such as images or videos:
:
This use of tensors to replace unit values is common in convolutional neural networks
A convolutional neural network (CNN) is a type of feedforward neural network that learns features via filter (or kernel) optimization. This type of deep learning network has been applied to process and make predictions from many different type ...
where each unit might be an image processed through multiple layers. By embedding the data in tensors such network structures enable learning of complex data types.
In fully connected layers
Tensors may also be used to compute the layers of a fully connected neural network, where the tensor is applied to the entire layer instead of individual unit values. The output value of single layer unit is the sum-product of its input units and the connection weights filtered through theactivation function
The activation function of a node in an artificial neural network is a function that calculates the output of the node based on its individual inputs and their weights. Nontrivial problems can be solved using only a few nodes if the activation f ...
:
:
The vectors and of output values can be expressed as a mode-1 tensors, while the hidden weights can be expressed as a mode-2 tensor. In this example the unit values are scalars while the tensor takes on the dimensions of the network layers:
:
:
:
In this notation, the output values can be computed as a tensor product of the input and weight tensors:
:
which computes the sum-product as a tensor multiplication (similar to matrix multiplication).
This formulation of tensors enables the entire layer of a fully connected network to be efficiently computed by mapping the units and weights to tensors.
In convolutional layers
A different reformulation of neural networks allows tensors to express the convolution layers of a neural network. A convolutional layer has multiple inputs, each of which is a spatial structure such as an image or volume. The inputs are convolved byfiltering
Filtration is a physical process that separates solid matter and fluid from a mixture.
Filter, filtering, filters or filtration may also refer to:
Science and technology
Computing
* Filter (higher-order function), in functional programming
* Fil ...
before being passed to the next layer. A typical use is to perform feature detection or isolation in image recognition.
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two ...
is often computed as the multiplication of an input signal with a filter kernel . In two dimensions the discrete, finite form is:
:
where is the width of the kernel.
This definition can be rephrased as a matrix-vector product in terms of tensors that express the kernel, data and inverse transform of the kernel.
:
where and are the inverse transform, data and kernel. The derivation is more complex when the filtering kernel also includes a non-linear activation function such as sigmoid or ReLU.
The hidden weights of the convolution layer are the parameters to the filter. These can be reduced with a pooling layer
In neural networks, a pooling layer is a kind of network layer that downsamples and aggregates information that is dispersed among many vectors into fewer vectors. It has several uses. It removes redundant information, reducing the amount of comp ...
which reduces the resolution (size) of the data, and can also be expressed as a tensor operation.
Tensor factorization
An important contribution of tensors in machine learning is the ability to factorize tensors to decompose data into constituent factors or reduce the learned parameters. Data tensor modeling techniques stem from the linear tensor decomposition (CANDECOMP/Parafac decomposition) and the multilinear tensor decompositions (Tucker).Tucker decomposition

Tucker decomposition
In mathematics, Tucker decomposition decomposes a tensor into a set of matrices and one small core tensor. It is named after Ledyard R. Tucker
although it goes back to Hitchcock in 1927.
Initially described as a three-mode extension of factor an ...
, for example, takes a 3-way array
and decomposes the tensor into three matrices and a smaller tensor . The shape of the matrices and new tensor are such that the total number of elements is reduced. The new tensors have shapes
:
:
:
:
Then the original tensor can be expressed as the tensor product of these four tensors:
:
In the example shown in the figure, the dimensions of the tensors are
: : I=8, J=6, K=3, : I=8, P=5, : J=6, Q=4, : K=3, R=2, : P=5, Q=4, R=2.
The total number of elements in the Tucker factorization is
:
:
The number of elements in the original is 144, resulting in a data reduction from 144 down to 110 elements, a reduction of 23% in parameters or data size. For much larger initial tensors, and depending on the rank (redundancy) of the tensor, the gains can be more significant.
The work of Rabanser et al. provides an introduction to tensors with more details on the extension of Tucker decomposition to N-dimensions beyond the mode-3 example given here.
Tensor trains
Another technique for decomposing tensors rewrites the initial tensor as a sequence (train) of smaller sized tensors. A tensor-train (TT) is a sequence of tensors of reduced rank, called ''canonical factors''. The original tensor can be expressed as the sum-product of the sequence. : Developed in 2011 by Ivan Oseledts, the author observes that Tucker decomposition is "suitable for small dimensions, especially for the three-dimensional case. For large ''d'' it is not suitable." Thus tensor-trains can be used to factorize larger tensors in higher dimensions.Tensor graphs
The unified data architecture and automatic differentiation of tensors has enabled higher-level designs of machine learning in the form of tensor graphs. This leads to new architectures, such as tensor-graph convolutional networks (TGCN), which identify highly non-linear associations in data, combine multiple relations, and scale gracefully, while remaining robust and performant. These developments are impacting all areas of machine learning, such as text mining and clustering, time varying data, and neural networks wherein the input data is a social graph and the data changes dynamically.Hardware
Tensors provide a unified way to train neural networks for more complex data sets. However, training is expensive to compute on classical CPU hardware. In 2014,Nvidia
Nvidia Corporation ( ) is an American multinational corporation and technology company headquartered in Santa Clara, California, and incorporated in Delaware. Founded in 1993 by Jensen Huang (president and CEO), Chris Malachowsky, and Curti ...
developecuDNN
CUDA Deep Neural Network, a library for a set of optimized primitives written in the parallel CUDA language. CUDA and thus cuDNN run on dedicated GPUs that implement unified massive parallelism in hardware. These GPUs were not yet dedicated chips for tensors, but rather existing hardware adapted for parallel computation in machine learning. In the period 2015–2017
Google
Google LLC (, ) is an American multinational corporation and technology company focusing on online advertising, search engine technology, cloud computing, computer software, quantum computing, e-commerce, consumer electronics, and artificial ...
invented the Tensor Processing Unit (TPU). TPUs are dedicated, fixed function hardware units that specialize in the matrix multiplications needed for tensor products. Specifically, they implement an array of 65,536 multiply units that can perform a 256x256 matrix sum-product in just one global instruction cycle.
Later in 2017, Nvidia released its own Tensor Core with the Volta GPU architecture. Each Tensor Core is a microunit that can perform a 4x4 matrix sum-product. There are eight tensor cores for each shared memory (SM) block. The first GV100 GPU card has 108 SMs resulting in 672 tensor cores. This device accelerated machine learning by 12x over the previous Tesla GPUs. The number of tensor cores scales as the number of cores and SM units continue to grow in each new generation of cards.
The development of GPU hardware, combined with the unified architecture of tensor cores, has enabled the training of much larger neural networks. In 2022, the largest neural network was Google's PaLM
Palm most commonly refers to:
* Palm of the hand, the central region of the front of the hand
* Palm plants, of family Arecaceae
** List of Arecaceae genera
**Palm oil
* Several other plants known as "palm"
Palm or Palms may also refer to:
Music ...
with 540 billion learned parameters (network weights) (the older GPT-3
Generative Pre-trained Transformer 3 (GPT-3) is a large language model released by OpenAI in 2020.
Like its predecessor, GPT-2, it is a decoder-only transformer model of deep neural network, which supersedes recurrence and convolution-based ...
language model has over 175 billion learned parameters that produces human-like text; size isn't everything, Stanford's much smaller 2023 Alpaca model claims to be better, having learned from Meta/Facebook's 2023 model LLaMA
The llama (; or ) (''Lama glama'') is a domesticated South American camelid, widely used as a List of meat animals, meat and pack animal by Inca empire, Andean cultures since the pre-Columbian era.
Llamas are social animals and live with ...
, the smaller 7 billion parameter variant). The widely popular chatbot ChatGPT
ChatGPT is a generative artificial intelligence chatbot developed by OpenAI and released on November 30, 2022. It uses large language models (LLMs) such as GPT-4o as well as other Multimodal learning, multimodal models to create human-like re ...
is built on top of GPT-3.5 (and after an update GPT-4
Generative Pre-trained Transformer 4 (GPT-4) is a multimodal large language model trained and created by OpenAI and the fourth in its series of GPT foundation models. It was launched on March 14, 2023, and made publicly available via the p ...
) using supervised and reinforcement learning.
References
{{reflist * Machine learning Tensors