Regression Slope on:
[Wikipedia]
[Google]
[Amazon]
In
 Given a
Given a
 Constant variance (a.k.a.
Constant variance (a.k.a. 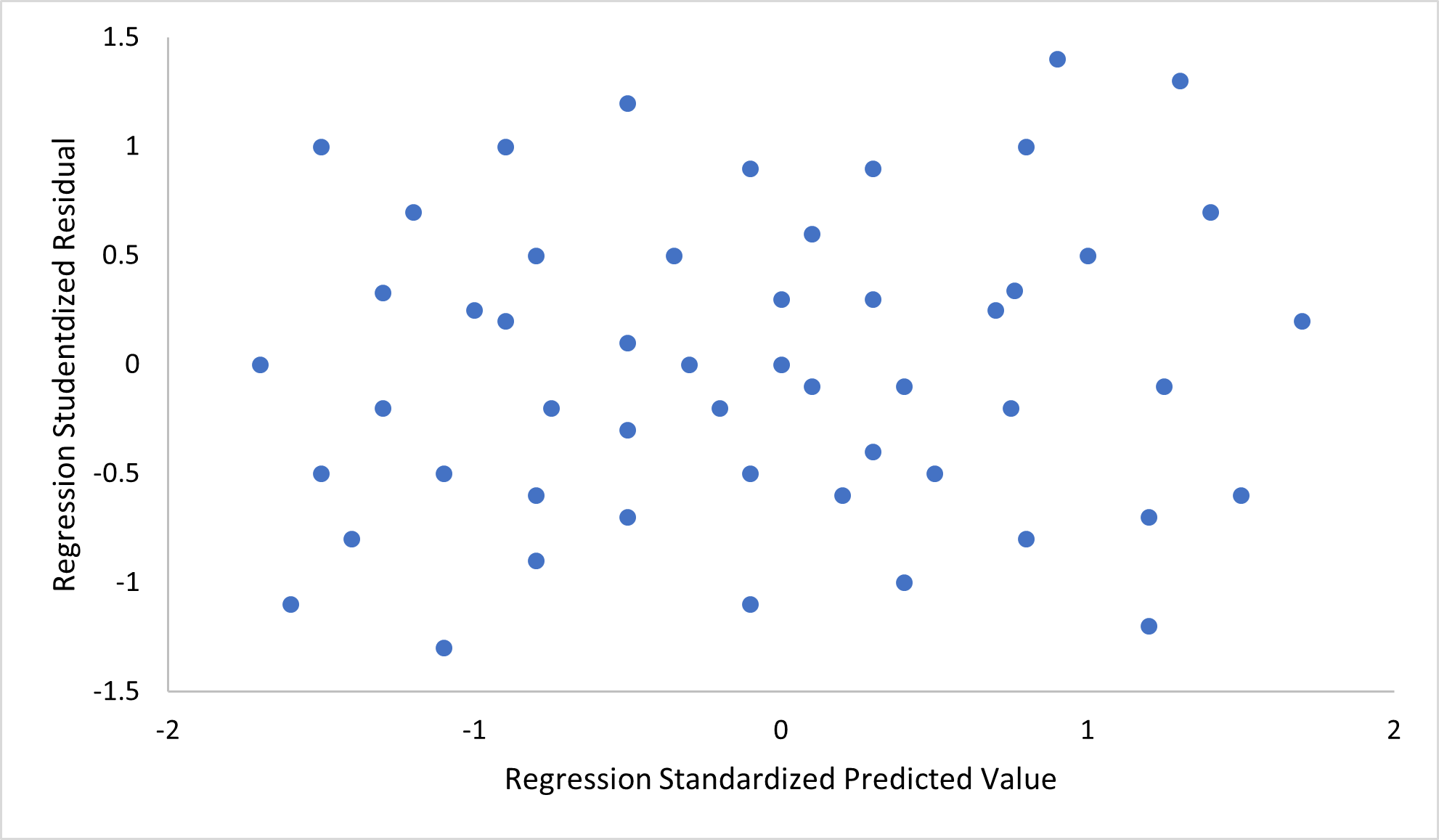 * Independence of errors. This assumes that the errors of the response variables are uncorrelated with each other. (Actual
* Independence of errors. This assumes that the errors of the response variables are uncorrelated with each other. (Actual
statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, linear regression is a model
A model is an informative representation of an object, person, or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin , .
Models can be divided in ...
that estimates the relationship between a scalar response (dependent variable
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical functio ...
) and one or more explanatory variables (regressor or independent variable
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function ...
). A model with exactly one explanatory variable is a ''simple linear regression
In statistics, simple linear regression (SLR) is a linear regression model with a single explanatory variable. That is, it concerns two-dimensional sample points with one independent variable and one dependent variable (conventionally, the ''x ...
''; a model with two or more explanatory variables is a multiple linear regression. This term is distinct from multivariate linear regression, which predicts multiple correlated
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistic ...
dependent variables rather than a single dependent variable.
In linear regression, the relationships are modeled using linear predictor function
In statistics and in machine learning, a linear predictor function is a linear function (linear combination) of a set of coefficients and explanatory variables (independent variables), whose value is used to predict the outcome of a dependent varia ...
s whose unknown model parameters are estimated
Estimation (or estimating) is the process of finding an estimate or approximation, which is a value that is usable for some purpose even if input data may be incomplete, uncertain, or unstable. The value is nonetheless usable because it is de ...
from the data
Data ( , ) are a collection of discrete or continuous values that convey information, describing the quantity, quality, fact, statistics, other basic units of meaning, or simply sequences of symbols that may be further interpreted for ...
. Most commonly, the conditional mean
In probability theory, the conditional expectation, conditional expected value, or conditional mean of a random variable is its expected value evaluated with respect to the conditional probability distribution. If the random variable can take on ...
of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''wikt:affine, affinis'', "connected with") is a geometric transformation that preserves line (geometry), lines and parallel (geometry), parallelism, but not necessarily ...
of those values; less commonly, the conditional median
The median of a set of numbers is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as the “ ...
or some other quantile
In statistics and probability, quantiles are cut points dividing the range of a probability distribution into continuous intervals with equal probabilities or dividing the observations in a sample in the same way. There is one fewer quantile t ...
is used. Like all forms of regression analysis, linear regression focuses on the conditional probability distribution
In probability theory and statistics, the conditional probability distribution is a probability distribution that describes the probability of an outcome given the occurrence of a particular event. Given two jointly distributed random variables X ...
of the response given the values of the predictors, rather than on the joint probability distribution
A joint or articulation (or articular surface) is the connection made between bones, ossicles, or other hard structures in the body which link an animal's skeletal system into a functional whole.Saladin, Ken. Anatomy & Physiology. 7th ed. McGraw- ...
of all of these variables, which is the domain of multivariate analysis
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable, i.e., '' multivariate random variables''.
Multivariate statistics concerns understanding the differ ...
.
Linear regression is also a type of machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
, more specifically a supervised algorithm, that learns from the labelled datasets and maps the data points to the most optimized linear functions that can be used for prediction on new datasets.
Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications. This is because models which depend linearly on their unknown parameters are easier to fit than models which are non-linearly related to their parameters and because the statistical properties of the resulting estimators are easier to determine.
Linear regression has many practical uses. Most applications fall into one of the following two broad categories:
* If the goal is error i.e. variance reduction
In mathematics, more specifically in the theory of Monte Carlo methods, variance reduction is a procedure used to increase the precision of the estimates obtained for a given simulation or computational effort. Every output random variable fr ...
in prediction
A prediction (Latin ''præ-'', "before," and ''dictum'', "something said") or forecast is a statement about a future event or about future data. Predictions are often, but not always, based upon experience or knowledge of forecasters. There ...
or forecasting
Forecasting is the process of making predictions based on past and present data. Later these can be compared with what actually happens. For example, a company might Estimation, estimate their revenue in the next year, then compare it against the ...
, linear regression can be used to fit a predictive model to an observed data set
A data set (or dataset) is a collection of data. In the case of tabular data, a data set corresponds to one or more table (database), database tables, where every column (database), column of a table represents a particular Variable (computer sci ...
of values of the response and explanatory variables. After developing such a model, if additional values of the explanatory variables are collected without an accompanying response value, the fitted model can be used to make a prediction of the response.
* If the goal is to explain variation in the response variable that can be attributed to variation in the explanatory variables, linear regression analysis can be applied to quantify the strength of the relationship between the response and the explanatory variables, and in particular to determine whether some explanatory variables may have no linear relationship with the response at all, or to identify which subsets of explanatory variables may contain redundant information about the response.
Linear regression models are often fitted using the least squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The me ...
approach, but they may also be fitted in other ways, such as by minimizing the " lack of fit" in some other norm
Norm, the Norm or NORM may refer to:
In academic disciplines
* Normativity, phenomenon of designating things as good or bad
* Norm (geology), an estimate of the idealised mineral content of a rock
* Norm (philosophy), a standard in normative e ...
(as with least absolute deviations
Least absolute deviations (LAD), also known as least absolute errors (LAE), least absolute residuals (LAR), or least absolute values (LAV), is a statistical optimality criterion and a statistical optimization technique based on minimizing the su ...
regression), or by minimizing a penalized version of the least squares cost function as in ridge regression
Ridge regression (also known as Tikhonov regularization, named for Andrey Tikhonov) is a method of estimating the coefficients of multiple- regression models in scenarios where the independent variables are highly correlated. It has been used in m ...
(''L''2-norm penalty) and lasso
A lasso or lazo ( or ), also called reata or la reata in Mexico, and in the United States riata or lariat (from Mexican Spanish lasso for roping cattle), is a loop of rope designed as a restraint to be thrown around a target and tightened when ...
(''L''1-norm penalty). Use of the Mean Squared Error
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference betwee ...
(MSE) as the cost on a dataset that has many large outliers, can result in a model that fits the outliers more than the true data due to the higher importance assigned by MSE to large errors. So, cost functions that are robust to outliers should be used if the dataset has many large outliers
In statistics, an outlier is a data point that differs significantly from other observations. An outlier may be due to a variability in the measurement, an indication of novel data, or it may be the result of experimental error; the latter ar ...
. Conversely, the least squares approach can be used to fit models that are not linear models. Thus, although the terms "least squares" and "linear model" are closely linked, they are not synonymous.
Formulation
data set
A data set (or dataset) is a collection of data. In the case of tabular data, a data set corresponds to one or more table (database), database tables, where every column (database), column of a table represents a particular Variable (computer sci ...
of ''n'' statistical unit
In statistics, a unit is one member of a set of entities being studied. It is the main source for the mathematical abstraction of a "random variable". Common examples of a unit would be a single person, animal, plant, manufactured item, or countr ...
s, a linear regression model assumes that the relationship between the dependent variable ''y'' and the vector of regressors x is linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
. This relationship is modeled through a ''disturbance term'' or ''error variable'' ''ε''—an unobserved random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
that adds "noise" to the linear relationship between the dependent variable and regressors. Thus the model takes the formwhere T denotes the transpose
In linear algebra, the transpose of a Matrix (mathematics), matrix is an operator which flips a matrix over its diagonal;
that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other ...
, so that x''i''T''β'' is the inner product
In mathematics, an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, ofte ...
between vectors x''i'' and ''β''.
Often these ''n'' equations are stacked together and written in matrix notation
In mathematics, a matrix (: matrices) is a rectangular array or table of numbers, symbols, or expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. ...
as
:
where
:
:
:
Notation and terminology
* is a vector of observed values of the variable called the ''regressand'', ''endogenous variable'', ''response variable'', ''target variable'', ''measured variable'', ''criterion variable'', or ''dependent variable
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical functio ...
''. This variable is also sometimes known as the ''predicted variable'', but this should not be confused with ''predicted values'', which are denoted . The decision as to which variable in a data set is modeled as the dependent variable and which are modeled as the independent variables may be based on a presumption that the value of one of the variables is caused by, or directly influenced by the other variables. Alternatively, there may be an operational reason to model one of the variables in terms of the others, in which case there need be no presumption of causality.
* may be seen as a matrix of row-vectors or of ''n''-dimensional column-vectors , which are known as ''regressors'', ''exogenous variables'', ''explanatory variables'', ''covariates'', ''input variables'', ''predictor variables'', or ''independent variables
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function ...
'' (not to be confused with the concept of independent random variables
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of ...
). The matrix is sometimes called the ''design matrix
In statistics and in particular in regression analysis, a design matrix, also known as model matrix or regressor matrix and often denoted by X, is a matrix of values of explanatory variables of a set of objects. Each row represents an individual o ...
''.
** Usually a constant is included as one of the regressors. In particular, for . The corresponding element of ''β'' is called the '' intercept''. Many statistical inference procedures for linear models require an intercept to be present, so it is often included even if theoretical considerations suggest that its value should be zero.
** Sometimes one of the regressors can be a non-linear function of another regressor or of the data values, as in polynomial regression
In statistics, polynomial regression is a form of regression analysis in which the relationship between the independent variable ''x'' and the dependent variable ''y'' is modeled as a polynomial in ''x''. Polynomial regression fits a nonlinear ...
and segmented regression
Segmented regression, also known as piecewise regression or broken-stick regression, is a method in regression analysis in which the independent variable is partitioned into intervals and a separate line segment is fit to each interval. Segmented ...
. The model remains linear as long as it is linear in the parameter vector ''β''.
** The values ''x''''ij'' may be viewed as either observed values of random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
s ''X''''j'' or as fixed values chosen prior to observing the dependent variable. Both interpretations may be appropriate in different cases, and they generally lead to the same estimation procedures; however different approaches to asymptotic analysis
In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing Limit (mathematics), limiting behavior.
As an illustration, suppose that we are interested in the properties of a function as becomes very larg ...
are used in these two situations.
* is a -dimensional ''parameter vector'', where is the intercept term (if one is included in the model—otherwise is ''p''-dimensional). Its elements are known as ''effects'' or ''regression coefficients'' (although the latter term is sometimes reserved for the ''estimated'' effects). In simple linear regression
In statistics, simple linear regression (SLR) is a linear regression model with a single explanatory variable. That is, it concerns two-dimensional sample points with one independent variable and one dependent variable (conventionally, the ''x ...
, ''p''=1, and the coefficient is known as ''regression slope''. Statistical estimation
Estimation (or estimating) is the process of finding an estimate or approximation, which is a value that is usable for some purpose even if input data may be incomplete, uncertain, or unstable. The value is nonetheless usable because it is d ...
and inference
Inferences are steps in logical reasoning, moving from premises to logical consequences; etymologically, the word '' infer'' means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinct ...
in linear regression focuses on ''β''. The elements of this parameter vector are interpreted as the partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). P ...
s of the dependent variable with respect to the various independent variables.
* is a vector of values . This part of the model is called the ''error term'', ''disturbance term'', or sometimes ''noise'' (in contrast with the "signal" provided by the rest of the model). This variable captures all other factors which influence the dependent variable ''y'' other than the regressors x. The relationship between the error term and the regressors, for example their correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics ...
, is a crucial consideration in formulating a linear regression model, as it will determine the appropriate estimation method.
Fitting a linear model to a given data set usually requires estimating the regression coefficients such that the error term is minimized. For example, it is common to use the sum of squared errors as a measure of for minimization.
Example
Consider a situation where a small ball is being tossed up in the air and then we measure its heights of ascent ''hi'' at various moments in time ''ti''. Physics tells us that, ignoring the drag, the relationship can be modeled as : where ''β''1 determines the initial velocity of the ball, ''β''2 is proportional to thestandard gravity
The standard acceleration of gravity or standard acceleration of free fall, often called simply standard gravity and denoted by or , is the nominal gravitational acceleration of an object in a vacuum near the surface of the Earth. It is a constant ...
, and ''ε''''i'' is due to measurement errors. Linear regression can be used to estimate the values of ''β''1 and ''β''2 from the measured data. This model is non-linear in the time variable, but it is linear in the parameters ''β''1 and ''β''2; if we take regressors x''i'' = (''x''''i''1, ''x''''i''2) = (''t''''i'', ''t''''i''2), the model takes on the standard form
:
Assumptions
Standard linear regression models with standard estimation techniques make a number of assumptions about the predictor variables, the response variable and their relationship. Numerous extensions have been developed that allow each of these assumptions to be relaxed (i.e. reduced to a weaker form), and in some cases eliminated entirely. Generally these extensions make the estimation procedure more complex and time-consuming, and may also require more data in order to produce an equally precise model. The following are the major assumptions made by standard linear regression models with standard estimation techniques (e.g.ordinary least squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship ...
):
* Weak exogeneity. This essentially means that the predictor variables ''x'' can be treated as fixed values, rather than random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
s. This means, for example, that the predictor variables are assumed to be error-free—that is, not contaminated with measurement errors. Although this assumption is not realistic in many settings, dropping it leads to significantly more difficult errors-in-variables models
In statistics, an errors-in-variables model or a measurement error model is a regression model that accounts for measurement errors in the independent variables. In contrast, standard regression models assume that those regressors have been me ...
.
* Linearity. This means that the mean of the response variable is a linear combination
In mathematics, a linear combination or superposition is an Expression (mathematics), expression constructed from a Set (mathematics), set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of ''x'' a ...
of the parameters (regression coefficients) and the predictor variables. Note that this assumption is much less restrictive than it may at first seem. Because the predictor variables are treated as fixed values (see above), linearity is really only a restriction on the parameters. The predictor variables themselves can be arbitrarily transformed, and in fact multiple copies of the same underlying predictor variable can be added, each one transformed differently. This technique is used, for example, in polynomial regression
In statistics, polynomial regression is a form of regression analysis in which the relationship between the independent variable ''x'' and the dependent variable ''y'' is modeled as a polynomial in ''x''. Polynomial regression fits a nonlinear ...
, which uses linear regression to fit the response variable as an arbitrary polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addit ...
function (up to a given degree) of a predictor variable. With this much flexibility, models such as polynomial regression often have "too much power", in that they tend to overfit the data. As a result, some kind of regularization must typically be used to prevent unreasonable solutions coming out of the estimation process. Common examples are ridge regression
Ridge regression (also known as Tikhonov regularization, named for Andrey Tikhonov) is a method of estimating the coefficients of multiple- regression models in scenarios where the independent variables are highly correlated. It has been used in m ...
and lasso regression. Bayesian linear regression
Bayesian linear regression is a type of conditional modeling in which the mean of one variable is described by a linear combination of other variables, with the goal of obtaining the posterior probability of the regression coefficients (as well ...
can also be used, which by its nature is more or less immune to the problem of overfitting. (In fact, ridge regression
Ridge regression (also known as Tikhonov regularization, named for Andrey Tikhonov) is a method of estimating the coefficients of multiple- regression models in scenarios where the independent variables are highly correlated. It has been used in m ...
and lasso regression can both be viewed as special cases of Bayesian linear regression, with particular types of prior distribution
A prior probability distribution of an uncertain quantity, simply called the prior, is its assumed probability distribution before some evidence is taken into account. For example, the prior could be the probability distribution representing the ...
s placed on the regression coefficients.)
*  Constant variance (a.k.a.
Constant variance (a.k.a. homoscedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as hete ...
). This means that the variance of the errors does not depend on the values of the predictor variables. Thus the variability of the responses for given fixed values of the predictors is the same regardless of how large or small the responses are. This is often not the case, as a variable whose mean is large will typically have a greater variance than one whose mean is small. For example, a person whose income is predicted to be $100,000 may easily have an actual income of $80,000 or $120,000—i.e., a standard deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean ( ...
of around $20,000—while another person with a predicted income of $10,000 is unlikely to have the same $20,000 standard deviation, since that would imply their actual income could vary anywhere between −$10,000 and $30,000. (In fact, as this shows, in many cases—often the same cases where the assumption of normally distributed errors fails—the variance or standard deviation should be predicted to be proportional to the mean, rather than constant.) The absence of homoscedasticity is called heteroscedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as hete ...
. In order to check this assumption, a plot of residuals versus predicted values (or the values of each individual predictor) can be examined for a "fanning effect" (i.e., increasing or decreasing vertical spread as one moves left to right on the plot). A plot of the absolute or squared residuals versus the predicted values (or each predictor) can also be examined for a trend or curvature. Formal tests can also be used; see Heteroscedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as hete ...
. The presence of heteroscedasticity will result in an overall "average" estimate of variance being used instead of one that takes into account the true variance structure. This leads to less precise (but in the case of ordinary least squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship ...
, not biased) parameter estimates and biased standard errors, resulting in misleading tests and interval estimates. The mean squared error
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference betwee ...
for the model will also be wrong. Various estimation techniques including weighted least squares
Weighted least squares (WLS), also known as weighted linear regression, is a generalization of ordinary least squares and linear regression in which knowledge of the unequal variance of observations (''heteroscedasticity'') is incorporated into ...
and the use of heteroscedasticity-consistent standard errors can handle heteroscedasticity in a quite general way. Bayesian linear regression
Bayesian linear regression is a type of conditional modeling in which the mean of one variable is described by a linear combination of other variables, with the goal of obtaining the posterior probability of the regression coefficients (as well ...
techniques can also be used when the variance is assumed to be a function of the mean. It is also possible in some cases to fix the problem by applying a transformation to the response variable (e.g., fitting the logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
of the response variable using a linear regression model, which implies that the response variable itself has a log-normal distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normal distribution, normally distributed. Thus, if the random variable is log-normally distributed ...
rather than a normal distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
f(x) = \frac ...
).
 * Independence of errors. This assumes that the errors of the response variables are uncorrelated with each other. (Actual
* Independence of errors. This assumes that the errors of the response variables are uncorrelated with each other. (Actual statistical independence
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of ...
is a stronger condition than mere lack of correlation and is often not needed, although it can be exploited if it is known to hold.) Some methods such as generalized least squares
In statistics, generalized least squares (GLS) is a method used to estimate the unknown parameters in a Linear regression, linear regression model. It is used when there is a non-zero amount of correlation between the Residual (statistics), resi ...
are capable of handling correlated errors, although they typically require significantly more data unless some sort of regularization is used to bias the model towards assuming uncorrelated errors. Bayesian linear regression
Bayesian linear regression is a type of conditional modeling in which the mean of one variable is described by a linear combination of other variables, with the goal of obtaining the posterior probability of the regression coefficients (as well ...
is a general way of handling this issue.
* Lack of perfect multicollinearity in the predictors. For standard least squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The me ...
estimation methods, the design matrix ''X'' must have full column rank ''p''; otherwise perfect multicollinearity
In statistics, multicollinearity or collinearity is a situation where the predictors in a regression model are linearly dependent.
Perfect multicollinearity refers to a situation where the predictive variables have an ''exact'' linear rela ...
exists in the predictor variables, meaning a linear relationship exists between two or more predictor variables. This can be caused by accidentally duplicating a variable in the data, using a linear transformation of a variable along with the original (e.g., the same temperature measurements expressed in Fahrenheit and Celsius), or including a linear combination of multiple variables in the model, such as their mean. It can also happen if there is too little data available compared to the number of parameters to be estimated (e.g., fewer data points than regression coefficients). Near violations of this assumption, where predictors are highly but not perfectly correlated, can reduce the precision of parameter estimates (see Variance inflation factor). In the case of perfect multicollinearity, the parameter vector ''β'' will be non-identifiable
In statistics, identifiability is a property which a statistical model, model must satisfy for precise statistical inference, inference to be possible. A model is identifiable if it is theoretically possible to learn the true values of this model ...
—it has no unique solution. In such a case, only some of the parameters can be identified (i.e., their values can only be estimated within some linear subspace of the full parameter space R''p''). See partial least squares regression. Methods for fitting linear models with multicollinearity have been developed, some of which require additional assumptions such as "effect sparsity"—that a large fraction of the effects are exactly zero. Note that the more computationally expensive iterated algorithms for parameter estimation, such as those used in generalized linear model
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by ...
s, do not suffer from this problem.
Violations of these assumptions can result in biased estimations of ''β'', biased standard errors, untrustworthy confidence intervals and significance tests. Beyond these assumptions, several other statistical properties of the data strongly influence the performance of different estimation methods:
* The statistical relationship between the error terms and the regressors plays an important role in determining whether an estimation procedure has desirable sampling properties such as being unbiased and consistent.
* The arrangement, or probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
of the predictor variables x has a major influence on the precision of estimates of ''β''. Sampling and design of experiments
The design of experiments (DOE), also known as experiment design or experimental design, is the design of any task that aims to describe and explain the variation of information under conditions that are hypothesized to reflect the variation. ...
are highly developed subfields of statistics that provide guidance for collecting data in such a way to achieve a precise estimate of ''β''.
Interpretation
A fitted linear regression model can be used to identify the relationship between a single predictor variable ''x''''j'' and the response variable ''y'' when all the other predictor variables in the model are "held fixed". Specifically, the interpretation of ''β''''j'' is the expected change in ''y'' for a one-unit change in ''x''''j'' when the other covariates are held fixed—that is, the expected value of thepartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). P ...
of ''y'' with respect to ''x''''j''. This is sometimes called the ''unique effect'' of ''x''''j'' on ''y''. In contrast, the ''marginal effect'' of ''x''''j'' on ''y'' can be assessed using a correlation coefficient
A correlation coefficient is a numerical measure of some type of linear correlation, meaning a statistical relationship between two variables. The variables may be two columns of a given data set of observations, often called a sample, or two c ...
or simple linear regression
In statistics, simple linear regression (SLR) is a linear regression model with a single explanatory variable. That is, it concerns two-dimensional sample points with one independent variable and one dependent variable (conventionally, the ''x ...
model relating only ''x''''j'' to ''y''; this effect is the total derivative
In mathematics, the total derivative of a function at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with res ...
of ''y'' with respect to ''x''''j''.
Care must be taken when interpreting regression results, as some of the regressors may not allow for marginal changes (such as dummy variables, or the intercept term), while others cannot be held fixed (recall the example from the introduction: it would be impossible to "hold ''ti'' fixed" and at the same time change the value of ''ti''2).
It is possible that the unique effect be nearly zero even when the marginal effect is large. This may imply that some other covariate captures all the information in ''x''''j'', so that once that variable is in the model, there is no contribution of ''x''''j'' to the variation in ''y''. Conversely, the unique effect of ''x''''j'' can be large while its marginal effect is nearly zero. This would happen if the other covariates explained a great deal of the variation of ''y'', but they mainly explain variation in a way that is complementary to what is captured by ''x''''j''. In this case, including the other variables in the model reduces the part of the variability of ''y'' that is unrelated to ''x''''j'', thereby strengthening the apparent relationship with ''x''''j''.
The meaning of the expression "held fixed" may depend on how the values of the predictor variables arise. If the experimenter directly sets the values of the predictor variables according to a study design, the comparisons of interest may literally correspond to comparisons among units whose predictor variables have been "held fixed" by the experimenter. Alternatively, the expression "held fixed" can refer to a selection that takes place in the context of data analysis. In this case, we "hold a variable fixed" by restricting our attention to the subsets of the data that happen to have a common value for the given predictor variable. This is the only interpretation of "held fixed" that can be used in an observational study
In fields such as epidemiology, social sciences, psychology and statistics, an observational study draws inferences from a sample (statistics), sample to a statistical population, population where the dependent and independent variables, independ ...
.
The notion of a "unique effect" is appealing when studying a complex system
A complex system is a system composed of many components that may interact with one another. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication sy ...
where multiple interrelated components influence the response variable. In some cases, it can literally be interpreted as the causal effect of an intervention that is linked to the value of a predictor variable. However, it has been argued that in many cases multiple regression analysis fails to clarify the relationships between the predictor variables and the response variable when the predictors are correlated with each other and are not assigned following a study design.
Extensions
Numerous extensions of linear regression have been developed, which allow some or all of the assumptions underlying the basic model to be relaxed.Simple and multiple linear regression
The simplest case of a single scalar predictor variable ''x'' and a single scalar response variable ''y'' is known as ''simple linear regression
In statistics, simple linear regression (SLR) is a linear regression model with a single explanatory variable. That is, it concerns two-dimensional sample points with one independent variable and one dependent variable (conventionally, the ''x ...
''. The extension to multiple and/or vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
-valued predictor variables (denoted with a capital ''X'') is known as multiple linear regression, also known as multivariable linear regression (not to be confused with '' multivariate linear regression'').
Multiple linear regression is a generalization of simple linear regression
In statistics, simple linear regression (SLR) is a linear regression model with a single explanatory variable. That is, it concerns two-dimensional sample points with one independent variable and one dependent variable (conventionally, the ''x ...
to the case of more than one independent variable, and a special case
In logic, especially as applied in mathematics, concept is a special case or specialization of concept precisely if every instance of is also an instance of but not vice versa, or equivalently, if is a generalization of .Brown, James Robert.� ...
of general linear models, restricted to one dependent variable. The basic model for multiple linear regression is
:
for each observation .
In the formula above we consider ''n'' observations of one dependent variable and ''p'' independent variables. Thus, ''Y''''i'' is the ''i''th observation of the dependent variable, ''X''''ij'' is ''i''th observation of the ''j''th independent variable, ''j'' = 1, 2, ..., ''p''. The values ''β''''j'' represent parameters to be estimated, and ''ε''''i'' is the ''i''th independent identically distributed normal error.
In the more general multivariate linear regression, there is one equation of the above form for each of ''m'' > 1 dependent variables that share the same set of explanatory variables and hence are estimated simultaneously with each other:
:
for all observations indexed as ''i'' = 1, ... , ''n'' and for all dependent variables indexed as ''j = 1, ... , ''m''.
Nearly all real-world regression models involve multiple predictors, and basic descriptions of linear regression are often phrased in terms of the multiple regression model. Note, however, that in these cases the response variable ''y'' is still a scalar. Another term, ''multivariate linear regression'', refers to cases where ''y'' is a vector, i.e., the same as ''general linear regression''.
Model Assumptions to Check:
1. Linearity: Relationship between each predictor and outcome must be linear
2. Normality of residuals: Residuals should follow a normal distribution
3. Homoscedasticity: Constant variance of residuals across predicted values
4. Independence: Observations should be independent (not repeated measures)
SPSS: Use partial plots, histograms, P-P plots, residual vs. predicted plots
General linear models
Thegeneral linear model
The general linear model or general multivariate regression model is a compact way of simultaneously writing several multiple linear regression models. In that sense it is not a separate statistical linear model. The various multiple linear regre ...
considers the situation when the response variable is not a scalar (for each observation) but a vector, y''i''. Conditional linearity of is still assumed, with a matrix ''B'' replacing the vector ''β'' of the classical linear regression model. Multivariate analogues of ordinary least squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship ...
(OLS) and generalized least squares
In statistics, generalized least squares (GLS) is a method used to estimate the unknown parameters in a Linear regression, linear regression model. It is used when there is a non-zero amount of correlation between the Residual (statistics), resi ...
(GLS) have been developed. "General linear models" are also called "multivariate linear models". These are not the same as multivariable linear models (also called "multiple linear models").
Heteroscedastic models
Various models have been created that allow forheteroscedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as hete ...
, i.e. the errors for different response variables may have different variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...
s. For example, weighted least squares
Weighted least squares (WLS), also known as weighted linear regression, is a generalization of ordinary least squares and linear regression in which knowledge of the unequal variance of observations (''heteroscedasticity'') is incorporated into ...
is a method for estimating linear regression models when the response variables may have different error variances, possibly with correlated errors. (See also Weighted linear least squares, and Generalized least squares
In statistics, generalized least squares (GLS) is a method used to estimate the unknown parameters in a Linear regression, linear regression model. It is used when there is a non-zero amount of correlation between the Residual (statistics), resi ...
.) Heteroscedasticity-consistent standard errors is an improved method for use with uncorrelated but potentially heteroscedastic errors.
Generalized linear models
TheGeneralized linear model
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by ...
(GLM) is a framework for modeling response variables that are bounded or discrete. This is used, for example:
* when modeling positive quantities (e.g. prices or populations) that vary over a large scale—which are better described using a skewed distribution
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real number, real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
For ...
such as the log-normal distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normal distribution, normally distributed. Thus, if the random variable is log-normally distributed ...
or Poisson distribution
In probability theory and statistics, the Poisson distribution () is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time if these events occur with a known const ...
(although GLMs are not used for log-normal data, instead the response variable is simply transformed using the logarithm function);
* when modeling categorical data
In statistics, a categorical variable (also called qualitative variable) is a variable (research), variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a ...
, such as the choice of a given candidate in an election (which is better described using a Bernoulli distribution
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli, is the discrete probability distribution of a random variable which takes the value 1 with probability p and the value 0 with pro ...
/binomial distribution
In probability theory and statistics, the binomial distribution with parameters and is the discrete probability distribution of the number of successes in a sequence of statistical independence, independent experiment (probability theory) ...
for binary choices, or a categorical distribution
In probability theory and statistics, a categorical distribution (also called a generalized Bernoulli distribution, multinoulli distribution) is a discrete probability distribution that describes the possible results of a random variable that can ...
/multinomial distribution In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a ''k''-sided die rolled ''n'' times. For ''n'' statistical independence, indepen ...
for multi-way choices), where there are a fixed number of choices that cannot be meaningfully ordered;
* when modeling ordinal data
Ordinal data is a categorical, statistical data type where the variables have natural, ordered categories and the distances between the categories are not known. These data exist on an ordinal scale, one of four Level of measurement, levels of m ...
, e.g. ratings on a scale from 0 to 5, where the different outcomes can be ordered but where the quantity itself may not have any absolute meaning (e.g. a rating of 4 may not be "twice as good" in any objective sense as a rating of 2, but simply indicates that it is better than 2 or 3 but not as good as 5).
Generalized linear models allow for an arbitrary ''link function'', ''g'', that relates the mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...
of the response variable(s) to the predictors: . The link function is often related to the distribution of the response, and in particular it typically has the effect of transforming between the range of the linear predictor and the range of the response variable.
Some common examples of GLMs are:
* Poisson regression
In statistics, Poisson regression is a generalized linear model form of regression analysis used to model count data and contingency tables. Poisson regression assumes the response variable ''Y'' has a Poisson distribution, and assumes the lo ...
for count data.
* Logistic regression
In statistics, a logistic model (or logit model) is a statistical model that models the logit, log-odds of an event as a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regres ...
and probit regression
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to e ...
for binary data.
* Multinomial logistic regression
In statistics, multinomial logistic regression is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than two possible discrete outcomes. That is, it is a model that is used to predict the prob ...
and multinomial probit
In statistics and econometrics, the multinomial probit model is a generalization of the probit model used when there are several possible categories that the dependent variable can fall into. As such, it is an alternative to the multinomial logi ...
regression for categorical data.
* Ordered logit and ordered probit regression for ordinal data.
Single index models allow some degree of nonlinearity in the relationship between ''x'' and ''y'', while preserving the central role of the linear predictor ''β''′''x'' as in the classical linear regression model. Under certain conditions, simply applying OLS to data from a single-index model will consistently estimate ''β'' up to a proportionality constant.
Hierarchical linear models
Hierarchical linear models (or ''multilevel regression'') organizes the data into a hierarchy of regressions, for example where ''A'' is regressed on ''B'', and ''B'' is regressed on ''C''. It is often used where the variables of interest have a natural hierarchical structure such as in educational statistics, where students are nested in classrooms, classrooms are nested in schools, and schools are nested in some administrative grouping, such as a school district. The response variable might be a measure of student achievement such as a test score, and different covariates would be collected at the classroom, school, and school district levels.Errors-in-variables
Errors-in-variables model
In statistics, an errors-in-variables model or a measurement error model is a regression model that accounts for measurement errors in the independent variables. In contrast, standard regression models assume that those regressors have been m ...
s (or "measurement error models") extend the traditional linear regression model to allow the predictor variables ''X'' to be observed with error. This error causes standard estimators of ''β'' to become biased. Generally, the form of bias is an attenuation, meaning that the effects are biased toward zero.
Group effects
In a multiple linear regression model : parameter of predictor variable represents the individual effect of . It has an interpretation as the expected change in the response variable when increases by one unit with other predictor variables held constant. When is strongly correlated with other predictor variables, it is improbable that can increase by one unit with other variables held constant. In this case, the interpretation of becomes problematic as it is based on an improbable condition, and the effect of cannot be evaluated in isolation. For a group of predictor variables, say, , a group effect is defined as a linear combination of their parameters : where is a weight vector satisfying . Because of the constraint on , is also referred to as a normalized group effect. A group effect has an interpretation as the expected change in when variables in the group change by the amount , respectively, at the same time with other variables (not in the group) held constant. It generalizes the individual effect of a variable to a group of variables in that () if , then the group effect reduces to an individual effect, and () if and for , then the group effect also reduces to an individual effect. A group effect is said to be meaningful if the underlying simultaneous changes of the variables is probable. Group effects provide a means to study the collective impact of strongly correlated predictor variables in linear regression models. Individual effects of such variables are not well-defined as their parameters do not have good interpretations. Furthermore, when the sample size is not large, none of their parameters can be accurately estimated by theleast squares regression
Linear least squares (LLS) is the least squares approximation of linear functions to data.
It is a set of formulations for solving statistical problems involved in linear regression, including variants for Ordinary least squares, ordinary (unweig ...
due to the multicollinearity
In statistics, multicollinearity or collinearity is a situation where the predictors in a regression model are linearly dependent.
Perfect multicollinearity refers to a situation where the predictive variables have an ''exact'' linear rela ...
problem. Nevertheless, there are meaningful group effects that have good interpretations and can be accurately estimated by the least squares regression. A simple way to identify these meaningful group effects is to use an all positive correlations (APC) arrangement of the strongly correlated variables under which pairwise correlations among these variables are all positive, and standardize all predictor variables in the model so that they all have mean zero and length one. To illustrate this, suppose that is a group of strongly correlated variables in an APC arrangement and that they are not strongly correlated with predictor variables outside the group. Let be the centred and be the standardized . Then, the standardized linear regression model is
:
Parameters in the original model, including , are simple functions of in the standardized model. The standardization of variables does not change their correlations, so is a group of strongly correlated variables in an APC arrangement and they are not strongly correlated with other predictor variables in the standardized model. A group effect of is
:
and its minimum-variance unbiased linear estimator is
:
where is the least squares estimator of . In particular, the average group effect of the standardized variables is
:
which has an interpretation as the expected change in when all in the strongly correlated group increase by th of a unit at the same time with variables outside the group held constant. With strong positive correlations and in standardized units, variables in the group are approximately equal, so they are likely to increase at the same time and in similar amount. Thus, the average group effect is a meaningful effect. It can be accurately estimated by its minimum-variance unbiased linear estimator , even when individually none of the can be accurately estimated by .
Not all group effects are meaningful or can be accurately estimated. For example, is a special group effect with weights and for , but it cannot be accurately estimated by . It is also not a meaningful effect. In general, for a group of strongly correlated predictor variables in an APC arrangement in the standardized model, group effects whose weight vectors are at or near the centre of the simplex () are meaningful and can be accurately estimated by their minimum-variance unbiased linear estimators. Effects with weight vectors far away from the centre are not meaningful as such weight vectors represent simultaneous changes of the variables that violate the strong positive correlations of the standardized variables in an APC arrangement. As such, they are not probable. These effects also cannot be accurately estimated.
Applications of the group effects include (1) estimation and inference for meaningful group effects on the response variable, (2) testing for "group significance" of the variables via testing versus , and (3) characterizing the region of the predictor variable space over which predictions by the least squares estimated model are accurate.
A group effect of the original variables can be expressed as a constant times a group effect of the standardized variables . The former is meaningful when the latter is. Thus meaningful group effects of the original variables can be found through meaningful group effects of the standardized variables.
Others
InDempster–Shafer theory
The theory of belief functions, also referred to as evidence theory or Dempster–Shafer theory (DST), is a general framework for reasoning with uncertainty, with understood connections to other frameworks such as probability, possibility and ...
, or a linear belief function in particular, a linear regression model may be represented as a partially swept matrix, which can be combined with similar matrices representing observations and other assumed normal distributions and state equations. The combination of swept or unswept matrices provides an alternative method for estimating linear regression models.
Estimation methods
A large number of procedures have been developed forparameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
estimation and inference in linear regression. These methods differ in computational simplicity of algorithms, presence of a closed-form solution
In mathematics, an expression or equation is in closed form if it is formed with constants, variables, and a set of functions considered as ''basic'' and connected by arithmetic operations (, and integer powers) and function composition. C ...
, robustness
Robustness is the property of being strong and healthy in constitution. When it is transposed into a system
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, ...
with respect to heavy-tailed distributions, and theoretical assumptions needed to validate desirable statistical properties such as consistency
In deductive logic, a consistent theory is one that does not lead to a logical contradiction. A theory T is consistent if there is no formula \varphi such that both \varphi and its negation \lnot\varphi are elements of the set of consequences ...
and asymptotic efficiency
Efficiency is the often measurable ability to avoid making mistakes or wasting materials, energy, efforts, money, and time while performing a task. In a more general sense, it is the ability to do things well, successfully, and without waste.
...
.
Some of the more common estimation techniques for linear regression are summarized below.
Least-squares estimation and related techniques
Assuming that the independent variables are