|
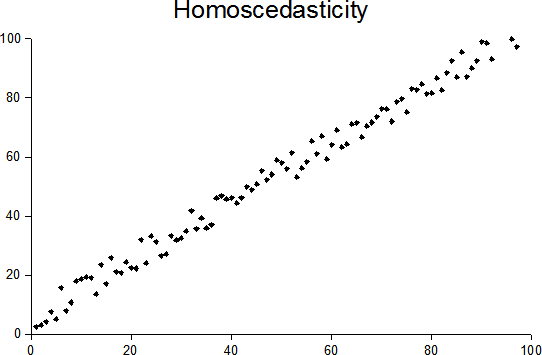
Homoscedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Variance
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the ''t''-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means. History While the analysis of variance reached fruition in the 20th century, antecedents extend centuries into the past according to Stigler. These include hypothesis testing, the partitioning of sums of squares, experimental techniques and the additive model. Laplace was performing hypothesis testi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss–Markov Theorem
In statistics, the Gauss–Markov theorem (or simply Gauss theorem for some authors) states that the ordinary least squares (OLS) estimator has the lowest sampling variance within the class of linear unbiased estimators, if the errors in the linear regression model are uncorrelated, have equal variances and expectation value of zero. The errors do not need to be normal, nor do they need to be independent and identically distributed (only uncorrelated with mean zero and homoscedastic with finite variance). The requirement that the estimator be unbiased cannot be dropped, since biased estimators exist with lower variance. See, for example, the James–Stein estimator (which also drops linearity), ridge regression, or simply any degenerate estimator. The theorem was named after Carl Friedrich Gauss and Andrey Markov, although Gauss' work significantly predates Markov's. But while Gauss derived the result under the assumption of independence and normality, Markov reduced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
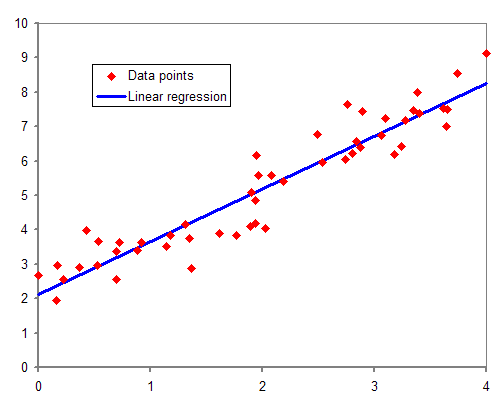
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression surface—the smaller the differences, the better the model fits the data. The resulting estimator can be expressed by a simple formula, especially in the case of a simple linear regression, in which there is a single regressor on the right side of the regression equation. The OLS estimator is con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Errors And Residuals In Statistics
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its " true value" (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the '' estimated'' value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals. In econometrics, "errors" are also called disturbances. Introduction Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression surface—the smaller the differences, the better the model fits the data. The resulting estimator can be expressed by a simple formula, especially in the case of a simple linear regression, in which there is a single regressor on the right side of the regression equation. The OLS estimator is con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Best Linear Unbiased Estimator
Best or The Best may refer to: People * Best (surname), people with the surname Best * Best (footballer, born 1968), retired Portuguese footballer Companies and organizations * Best & Co., an 1879–1971 clothing chain * Best Lock Corporation, a lock manufacturer * Best Manufacturing Company, a farm machinery company * Best Products, a chain of catalog showroom retail stores * Brihanmumbai Electric Supply and Transport, a public transport and utility provider * Best High School (other) Acronyms * Berkeley Earth Surface Temperature, a project to assess global temperature records * BEST Robotics, a student competition * BioEthanol for Sustainable Transport * Bootstrap error-adjusted single-sample technique, a statistical method * Bringing Examination and Search Together, a European Patent Office initiative * Bronx Environmental Stewardship Training, a program of the Sustainable South Bronx organization * Smart BEST, a Japanese experimental train * Brihanmumbai Electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Engle
Robert Fry Engle III (born November 10, 1942) is an American economist and statistician. He won the 2003 Nobel Memorial Prize in Economic Sciences, sharing the award with Clive Granger, "for methods of analyzing economic time series with time-varying volatility (ARCH)". Biography Engle was born in Syracuse, New York into Quaker family and went on to graduate from Williams College with a BS in physics. He earned an MS in physics and a PhD in economics, both from Cornell University in 1966 and 1969 respectively. After completing his PhD, Engle became an economics professor at the Massachusetts Institute of Technology from 1969 to 1977. He joined the faculty of the University of California, San Diego (UCSD) in 1975, wherefrom he retired in 2003. He now holds positions of Professor Emeritus and Research Professor at UCSD. He currently teaches at New York University, Stern School of Business where he is the Michael Armellino professor in Management of Financial Services. At New Yor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
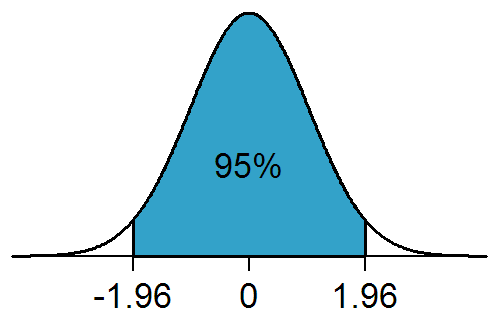
Statistical Significance
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scedastic Function
In probability theory and statistics, a conditional variance is the variance of a random variable given the value(s) of one or more other variables. Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function. Conditional variances are important parts of autoregressive conditional heteroskedasticity (ARCH) models. Definition The conditional variance of a random variable ''Y'' given another random variable ''X'' is :\operatorname(Y, X) = \operatorname\Big(\big(Y - \operatorname(Y\mid X)\big)^\mid X\Big). The conditional variance tells us how much variance is left if we use \operatorname(Y\mid X) to "predict" ''Y''. Here, as usual, \operatorname(Y\mid X) stands for the conditional expectation of ''Y'' given ''X'', which we may recall, is a random variable itself (a function of ''X'', determined up to probability one). As a result, \operatorname(Y, X) itself is a random variable (and is a function of ''X''). Explanation, rel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |