Prospect theory

Prospect theory is a theory of behavioral economics, judgment and decision making that was developed by Daniel Kahneman and Amos Tversky in 1979. The theory was cited in the decision to award Kahneman the 2002 Nobel Memorial Prize in Economics.

Based on results from controlled studies, it describes how individuals assess their loss and gain perspectives in an asymmetric manner (see loss aversion). For example, for some individuals, the pain from losing $1,000 could only be compensated by the pleasure of earning $2,000. Thus, contrary to the expected utility theory (which models the decision that perfectly rational agents would make), prospect theory aims to describe the actual behavior of people.

In the original formulation of the theory, the term ''prospect'' referred to the predictable results of a lottery. However, prospect theory can also be applied to the prediction of other forms of behaviors and decisions.

Prospect theory challenges the expected utility theory developed by John von Neumann and Oskar Morgenstern in 1944 and constitutes one of the first economic theories built using experimental methods.

History

In the draft received by the economist Richard Thaler in 1976, the term "Value Theory" was used instead of Prospect Theory. Later on, Kahneman and Tversky changed the title to Prospect Theory to avoid possible confusions. According to Kahneman, the new title was 'meaningless.'

Overview

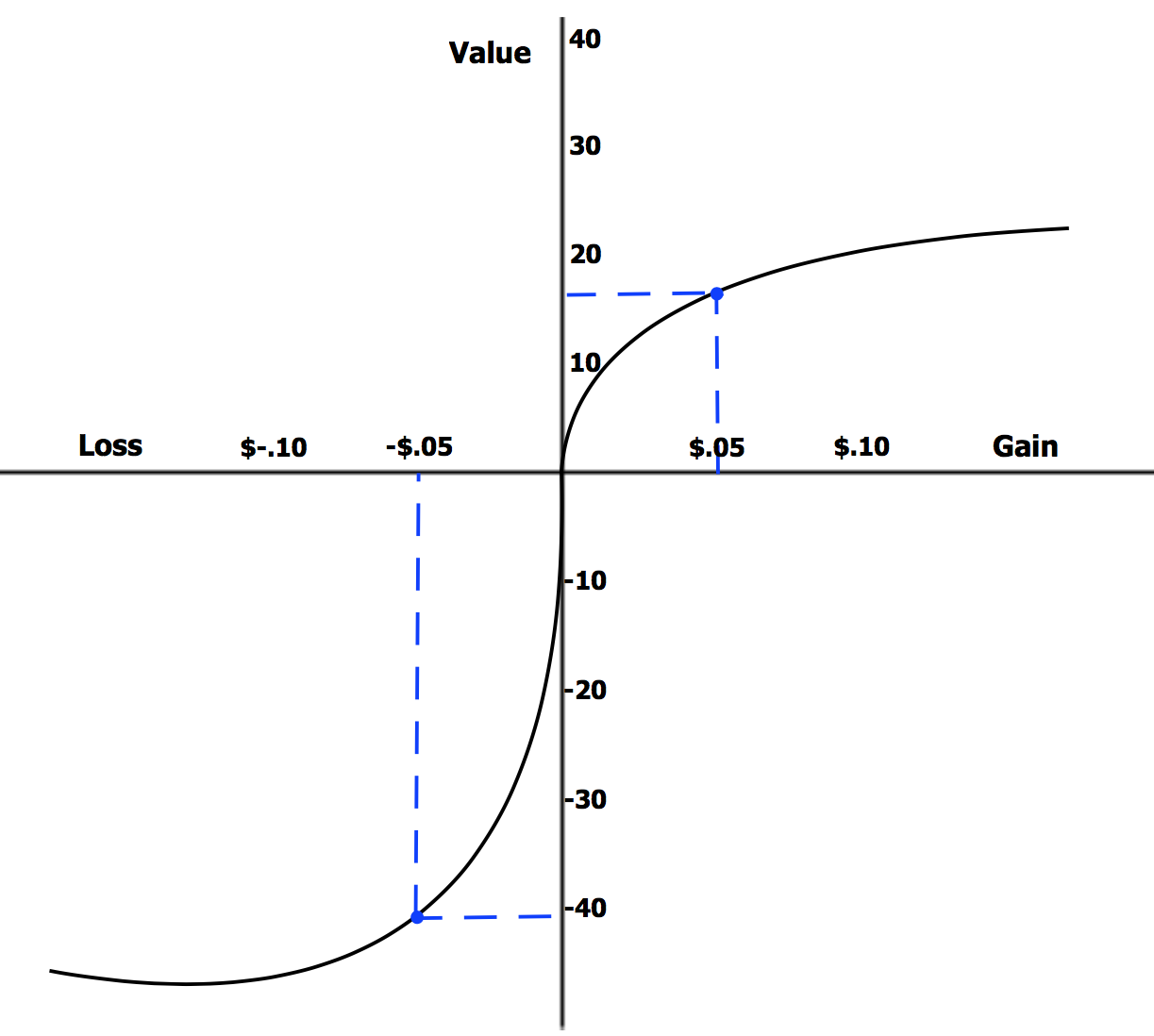
Prospect theory stems from loss aversion, where the observation is that agents asymmetrically feel losses greater than that of an equivalent gain. It centralises around the idea that people conclude their utility from gains and losses relative to a certain "neutral" reference point regarding their current individual situation. Thus, rather than making decisions like a rational agent maximizing a fixed expected utility, value decisions are made relative to the current neutral situation, not following any absolute measure of utility.

Consider two scenarios;

# 100% chance to gain $450 or 50% chance to gain $1000
# 100% chance to lose $500 or 50% chance to lose $1100

It is assumed that the agent's individual utility is proportional to the dollar amount (e.g. $1000 would be twice as useful as $500). Prospect theory suggests that;

* When faced with a risky choice leading to gains, agents are ''risk averse'', preferring the certain outcome with a lower expected utility ( concave value function).
** ''Agents will choose the certain $450 even though the expected utility of the risky gain is higher''
* When faced with a risky choice leading to losses agents are ''risk seeking'', preferring the outcome that has a lower expected utility but the potential to avoid losses ( convex value function).
** ''Agents will choose the 50% chance to lose $1100 even though the expected utility is lower, due to the chance that they lose nothing at all''

These two examples are thus in contradiction with the theory of expected utility, which leads only to choices with the maximum utility. Also, the concavity for gains and convexity for losses implies diminishing marginal utility with increasing gains/losses. In other words, someone who has more money has a lower desire for a fixed amount of gain (and lower aversion to a fixed amount of loss) than someone who has less money.

The theory continues with a second concept, based on the observation that people attribute excessive weight to events with low probability and insufficient weight to events with high probability. For example, individuals may unconsciously treat an outcome with a probability of 99% as if its probability were 95%, and an outcome with probability of 1% as if it had a probability of 5%. Under- and over-weighting of probabilities is importantly distinct from under- and over-estimating probabilities, a different type of cognitive bias observed for example in the overconfidence effect.

Model

The theory describes the decision processes in two stages:
*During an initial phase termed ''editing'', outcomes of a decision are ordered according to a certain heuristic. In particular, people decide which outcomes they consider equivalent, set a reference point and then consider lesser outcomes as losses and greater ones as gains. The editing phase aims to alleviate any framing effects. It also aims to resolve isolation effects stemming from individuals' propensity to often isolate consecutive probabilities instead of treating them together. The editing process can be viewed as composed of coding, combination, segregation, cancellation, simplification and detection of dominance.
*In the subsequent ''evaluation'' phase, people behave as if they would compute a value ( utility), based on the potential outcomes and their respective probabilities, and then choose the alternative having a higher utility.

The formula that Kahneman and Tversky assume for the evaluation phase is (in its simplest form) given by:

:$V = \sum_^n \pi(p_i)v(x_i)$

where $V$ is the overall or expected utility of the outcomes to the individual making the decision, $x_1,x_2,\ldots,x_n$ are the potential outcomes and $p_1,p_2,\dots,p_n$ their respective probabilities and $v$ is a function that assigns a value to an outcome. The value function that passes through the reference point is s-shaped and asymmetrical. Losses hurt more than gains feel good (loss aversion). This differs from expected utility theory, in which a rational agent is indifferent to the reference point. In expected utility theory, the individual does not care how the outcome of losses and gains are framed. The function $\pi$ is a probability weighting function and captures the idea that people tend to overreact to small probability events, but underreact to large probabilities. Let $(x,p;y,q)$ denote a prospect with outcome $x$ with probability $p$ and outcome $y$ with probability $q$ and nothing with probability $1-p-q$. If $(x,p;y,q)$ is a regular prospect (i.e., either $p+q<1$, or $x \geq 0 \geq y$, or $x \leq 0 \leq y$), then:

$V(x,p;y,q)=\pi(p)\nu(x)+\pi(q)\nu(y)$

However, if $p+q=1$ and either $x>y>0$ or x, then:

V(x,p;y,q)=\nu(y)+\pi(p) \left \nu (x)- \nu (y) \right/math>

It can be deduced from the first equation that $\nu(y)+\nu(-y)>\nu(x)+\nu(-x)$ and $\nu(-y)+\nu(-x)>\nu(x)+\nu(-x)$. The value function is thus defined on deviations from the reference point, generally concave for gains and commonly convex for losses and steeper for losses than for gains. If $(x,p)$ is equivalent to $(y,pq)$ then $(x,pr)$ is not preferred to $(y,pqr)$, but from the first equation it follows that $\pi(p)\nu(x)+\pi(pq)\nu(y)=\pi(pq)\nu(y)$, which leads to $\pi(pr)\nu(x) \leq \pi(pqr)\nu(y)$, therefore:

$\frac\leq\frac$

This means that for a fixed ratio of probabilities the decision weights are closer to unity when probabilities are low than when they are high. In prospect theory, $\pi$ is never linear. In the case that $x>y>0$, $p>p'$ and $p+q=p'+q'<1,$ prospect $(x,p';y,q)$ dominates prospect $(x,p';y,q')$, which means that $\pi(p)\nu(x)+\pi(q)\nu(y)>\pi(p')\nu(x)+\pi(q')\nu(y)$, therefore:

$\frac\leq \frac$

As $y \rightarrow x$, $\pi(p)-\pi(p') \rightarrow \pi(q')-\pi(q)$, but since $p-p'=q'-q$, it would imply that $\pi$ must be linear; however, dominated alternatives are brought to the evaluation phase since they are eliminated in the editing phase. Although direct violations of dominance never happen in prospect theory, it is possible that a prospect A dominates B, B dominates C but C dominates A.

Example

To see how prospect theory can be applied, consider the decision to buy insurance. Assume the probability of the insured risk is 1%, the potential loss is $1,000 and the premium is $15. If we apply prospect theory, we first need to set a reference point. This could be the current wealth or the worst case (losing $1,000). If we set the frame to the current wealth, the decision would be to either

1. Pay $15 for insurance, which yields a prospect-utility of $v(-15)$,

OR

2. Enter a lottery with possible outcomes of $0 (probability 99%) or −$1,000 (probability 1%), which yields a prospect-utility of $\pi(0.01) \times v(-1000) + \pi(0.99) \times v(0) = \pi(0.01) \times v(-1000)$.

According to prospect theory,

* $\pi(0.01) > 0.01$, because low probabilities are usually overweighted;
* $v(-15) / v(-1000) > 0.015$, by the convexity of value function in losses.

The comparison between $\pi(0.01)$ and $v(-15) / v(-1000)$ is not immediately evident. However, for typical value and weighting functions, $\pi(0.01)>v(-15) / v(-1000)$, and hence $\pi(0.01) \times v(-1000) < v(-15)$. That is, a strong overweighting of small probabilities is likely to undo the effect of the convexity of $v$ in losses, making the insurance attractive.

If we set the frame to -$1,000, we have a choice between $v(985)$ and $\pi(0.99) \times v(1000)$. In this case, the concavity of the value function in gains and the underweighting of high probabilities can also lead to a preference for buying the insurance.

The interplay of overweighting of small probabilities and concavity-convexity of the value function leads to the so-called ''fourfold pattern of risk attitudes'': risk-averse behavior when gains have moderate probabilities or losses have small probabilities; risk-seeking behavior when losses have moderate probabilities or gains have small probabilities.

Below is an example of the fourfold pattern of risk attitudes. The first item in each quadrant shows an example prospect (e.g. 95% chance to win $10,000 is high probability and a gain). The second item in the quadrant shows the focal emotion that the prospect is likely to evoke. The third item indicates how most people would behave given each of the prospects (either Risk Averse or Risk Seeking). The fourth item states expected attitudes of a potential defendant and plaintiff in discussions of settling a civil suit.

Probability distortion is that people generally do not look at the value of probability uniformly between 0 and 1. Lower probability is said to be over-weighted (that is, a person is overly concerned with the outcome of the probability) while medium to high probability is under-weighted (that is, a person is not concerned enough with the outcome of the probability). The exact point in which probability goes from over-weighted to under-weighted is arbitrary, but a good point to consider is probability = 0.33. A person values probability = 0.01 much more than the value of probability = 0 (probability = 0.01 is said to be over-weighted). However, a person has about the same value for probability = 0.4 and probability = 0.5. Also, the value of probability = 0.99 is much less than the value of probability = 1, a sure thing (probability = 0.99 is under-weighted). A little more in depth when looking at probability distortion is that ''π''(''p'') + ''π''(1 − ''p'') < 1 (where ''π''(''p'') is probability in prospect theory).

Myopic Loss Aversion (MLA)

Myopic loss aversion (MLA), a concept derived from prospect theory, refers to the natural tendency of humans to focus on short-term losses and gains and to weigh them more heavily than long-term losses and gains. This bias can lead to seemingly poorer decision making, as individuals may focus towards avoiding immediate losses instead of achieving long-term gains.

A prolific study that examined myopic loss aversion was conducted by Gneezy and Potters in 1997. In this study, participants engaged in a straightforward betting game in which they could either place a bet on a coin landing , or they could choose to not bet at all. The participants were provided with a fixed amount of money, and held the task to maximize their earnings over a series of rounds.

The results of the study exhibited that participants were more likely to place a bet when they had just lost money in the previous round, and they were more likely to avoid a bet when they had just won money in the previous round. This behavior is consistent with myopic loss aversion theory, as the participants were placing greater magnitude on their short-term gains and losses instead of their overall earnings over the course of the study.

Additionally, the findings revealed that the participants that were provided with a higher amount of money at the beginning of the study tended to be more risk-averse than those who were given a lower starting amount. This observation supports the concept of diminishing sensitivity to changes in wealth predicted by prospect theory.

Overall, the study by Gneezy and Potters emphasizes the existence of myopic loss aversion, demonstrating how this bias can result in non-optimal decisions. By analyzing how prospect theory and myopic loss aversion influence decision-making, it provides the ability for researchers and policymakers to create interventions that help people make more informed choices and attain their long-term goals.

When referring to investment decisions, myopic loss aversion has the ability to lead to investment decisions that can be of a more conservative approach. For instance, investors potentially overreact to dips in stock prices in their stock portfolio, which causes feelings of fear and anxiety of profit loss. This reaction from investors has the ability to lead in a loss in profit due to selling off their stock. Studies in behavioral finance analyzed this pattern, observing that there is a tendency to avoid high-reward options in the market, as the risk of short-term loss potentially influences the broker.

Acclaimed behavioral economists Benartzi and Thaler analyzed this concept, calling it the "equity premium puzzle." This puzzle refers to the fact that stocks, in terms of historical statistics, exceed profits in comparison to bonds over extended periods of time. More interestingly, they observed that newer investors tend not to emphasize stocks over bonds. This phenomenon has been linked by Benartzi and Thaler to myopic loss aversion due to the lack of emphasis on stocks by young investors, as young investors tended to abandon stocks due to minor dips in the market.

This behavior can lead to a decreases market predictability, as investors act on short-term losses by selling their stocks, there can be a ripple effect that intensifies dips in the economy. As investors that are heavily influenced by the market decline sell their stocks, the now increased amount of shares due to mass sell-offs further lower prices. This hypothetical community of investors react along with falling stock prices, causing them to sell, potentially causing the stock price to lower as a whole. This concept, investor anxiety, can potentially emphasize the want to sell of investments for security reasons, regardless of long-term profit potential. This constant market fluctuation is directly related to market stability.

An example of this effect was seen during economic crises such as the 2008 financial crash, when panic induced sell-offs heavily impacted market stability. The period prior to the Great Recession had a "decade-long expansion in US housing market activity peaked in 2006," which came to a halt in 2007. As the trends prior to 2008 hinted at the fall of mortgage pricing, real-estate investors reacted promptly. The mass sell-offs of mortgaged-backed investments led to a similar instability in other markets, including credit markets, and the stock market.

Applications

Economics

Some behaviors observed in economics, like the disposition effect or the reversing of risk aversion/ risk seeking in case of gains or losses (termed the ''reflection effect''), can also be explained by referring to the prospect theory.

An important implication of prospect theory is that the way economic agents subjectively frame an outcome or transaction in their mind affects the utility they expect or receive. Narrow framing is a derivative result which has been documented in experimental settings by Tversky and Kahneman, whereby people evaluate new gambles in isolation, ignoring other relevant risks. This phenomenon can be seen in practice in the reaction of people to stock market fluctuations in comparison with other aspects of their overall wealth; people are more sensitive to spikes in the stock market as opposed to their labor income or the housing market. It has also been shown that narrow framing causes loss aversion among stock market investors. And the work of Tversky and Kahneman is largely responsible for the advent of behavioral economics, and is used extensively in mental accounting.Pesendorfer, Wolfgang. 2006. "Behavioral Economics Comes of Age: A Review Essay on ''Advances in Behavioral Economics''." Journal of Economic Literature, 44 (3): 712–721.

Software

The digital age has brought the implementation of prospect theory in software. Framing and prospect theory has been applied to a diverse range of situations which appear inconsistent with standard economic rationality: the equity premium puzzle, the excess returns puzzle and long swings/PPP puzzle of exchange rates through the endogenous prospect theory of Imperfect Knowledge Economics, the status quo bias, various gambling and betting puzzles, intertemporal consumption, and the endowment effect. It has also been argued that prospect theory can explain several empirical regularities observed in the context of auctions (such as secret reserve prices) which are difficult to reconcile with standard economic theory.

Online pay-per bid auction sites are a classic example of decision making under risk. Previous attempts at predicting consumer behavior have shown that utility theory does not sufficiently describe decision making under risk. When prospect theory was added to a previously existing model that was attempting to explain consumer behavior during auctions, out-of-sample predictions were shown to be more accurate than a corresponding expected utility model. Specifically, prospect theory was boiled down to certain elements: preference, loss aversion and probability weighting. These elements were then used to find a backward solution on 537,045 auctions. The greater accuracy may be explained by the new model having the ability to correct for two behavioral irrationalities: The sunk cost fallacy and average auctioneer revenues above current retail price. These findings would also imply that the using prospect theory as a descriptive theory of decision making under risk is also accurate in situations where risk arises through the interactions of different people.

Politics

Given the necessary degree of uncertainty for which prospect theory is applied, it should come as no surprise that it and other psychological models are applied extensively in the context of political decision-making. Both rational choice and game theoretical models generate significant predictive power in the analysis of politics and international relations (IR). But prospect theory, unlike the alternative models, (1) is "founded on empirical data", (2) allows and accounts for dynamic change, (3) addresses previously-ignored modular elements, (4) emphasizes the situation in the decision-making process, (5) "provides a micro-foundational basis for the explanation of larger phenomena", and (6) stresses the importance of loss in utility and value calculations. Moreover, again unlike other models, prospect theory "asks different sorts of questions, seeks different evidence, and reaches different conclusions." However, there exist shortcomings inherent in prospect theory's political application, such as the dilemma regarding an actor's perceived position on the gain-loss domain spectrum, and the discordance between ideological and pragmatic (i.e. 'in the lab' versus 'in the field') assessments of an actor's propensity toward seeking or avoiding risk.

That said, political scientists have applied prospect theory to a wide range of issues in domestic and comparative politics. For example, they have found that politicians are more likely to phrase a radical economic policy as one ensuring 90% employment rather than 10% unemployment, because framing it as the former puts the citizenry in a "domain of gain," which is thereby conducive to greater populace satisfaction. On a broader scale: Consider an administration debating the implementation of a controversial reform, and that such a reform yields a small chance for a widespread revolt. " e disutility induced by loss aversion," even with minute probabilities of said insurrection, will dissuade the government from moving forward with the reform.

Scholars have employed prospect theory to shed light on a number of issue areas in politics. For example, Kurt Weyland finds that political leaders do not always undertake bold and politically risky domestic initiatives when they are at the pinnacle of their power. Instead, such policies often appear to be risky gambits initiated by politically vulnerable regimes. He suggests that in Latin America, politically weakened governments were more likely to implement fundamental and economically painful market-oriented reforms, even though they were more vulnerable to political backlash. Barbara Vis and Kees van Kersbergen have reached a similar conclusion in their investigation of Italian welfare reforms.

Maria Fanis uses prospect theory to show how risk acceptance can help domestic groups overcome collective action problems inherent to coalition building. She suggests that collective action is more likely in a perceive domain of loss because individuals become more willing to accept the risk of free riding by others. In Chile, this process led domestic interest groups to form unlikely political coalitions. Zeynep Somer-Topcu's research suggests that political parties respond more strongly to electoral defeat than to success in the next election cycle. As prospect theory predicts, parties are more likely to shift their policies in response to a vote loss in the previous election cycle compared to a vote gain. Lawrence Kuznar and James Lutz find that loss frames can increase support of individuals for terrorist groups.

International relations

International relations theorists have applied prospect theory to a wide range of issues in world politics, especially security-related matters. For example, in war-time, policy-makers, when in a perceived domain of loss, are more likely to take risks that would otherwise have been avoided, e.g. "gambling on a risky rescue mission", or implementing radical domestic reform to support military efforts.

Early applications of prospect theory in International Relations emphasized the potential to explain anomalies in foreign policy decision-making that remained difficult to account for on the basis of rational choice theory. They developed detailed qualitative case studies of specific foreign policy decisions to explore the role of framing effects in choice selection. For example, Rose McDermott applied prospect theory to a series of case studies in American foreign policy, including the Suez Crisis in 1956, the U-2 Crisis in 1960, the U.S. decision to admit the Iranian shah to the United States in 1979, and the U.S. decision to carry out a hostage rescue mission in 1980. Jeffrey Berejikian employed prospect theory to analyze the genesis of the Montreal Protocol, a landmark environmental agreement.

William Boettcher integrated elements of prospect theory with psychological research on personality dispositions to construct a “Risk Explanation Framework,” which he used to analyze foreign-policy decision making. He then evaluated the framework against six case studies on presidential foreign policy decision-making.

Insurance

Applications of prospect theory in the context of insurance seek to explain the consumer choices. Syndor (2010) suggests that the probability weighting aspect of prospect theory aims to explain the behaviour of the consumers who choose a higher premium for a reduced deductible even when the annualised claim rate is very low (approximately 5%). In a study of 50,000 customers, they had four options for the deductibles on their policy; $100, $250, $500, $1000. From this it was found that a $500 deductible resulted in a $715 annual premium and $1000 deductible being $615. The customers that chose the $500 deductible were paying an additional $100 per year even though the chance that a claim will be made is extremely low, and the deductible be paid. Under the expected utility framework, this can only be realised through high levels of risk aversion. Households place a greater weight on the probability that a claim will be made when choosing a policy, thus it is suggested that the reference point of the household significantly influences the decisions when it comes to premiums and deductibles. This is consistent with the theory that people assign excessive weight to scenarios with low probabilities and insufficient weight to events with high probability.

Limits and extensions

The original version of prospect theory gave rise to violations of first-order stochastic dominance. That is, prospect A might be preferred to prospect B even if the probability of receiving a value x or greater is at least as high under prospect B as it is under prospect A for all values of x, and is greater for some value of x. Later theoretical improvements overcame this problem, but at the cost of introducing intransitivity in preferences. A revised version, called cumulative prospect theory overcame this problem by using a probability weighting function derived from rank-dependent expected utility theory. Cumulative prospect theory can also be used for infinitely many or even continuous outcomes (for example, if the outcome can be any real number). An alternative solution to overcome these problems within the framework of (classical) prospect theory has been suggested as well.

The reference point in the prospect theory inverse s-shaped graph also could lead to limitations due to it possibly being discontinuous at that point and having a geometric violation. This would lead to limitations in regards to accounting for the zero-outcome effect, the absence of behavioral conditionality in risky decisions as well as limitations in deriving the curve. A transitionary concave-convex universal system was proposed to eliminate this limitation.

Critics from the field of psychology argued that even if Prospect Theory arose as a descriptive model, it offers no psychological explanations for the processes stated in it.
Furthermore, factors that are equally important to decision making processes have not been included in the model, such as emotion.

A relatively simple ad hoc decision strategy, the priority heuristic, has been suggested as an alternative model. While it can predict the majority choice in all (one-stage) gambles in Kahneman and Tversky (1979), and predicts the majority choice better than cumulative prospect theory across four different data sets with a total of 260 problems, this heuristic, however, fails to predict many simple decision situations that are typically not tested in experiments and it also does not explain heterogeneity between subjects.

An international survey in 53 countries, published in '' Theory and Decision'' in 2017, confirmed that prospect theory describes decisions on lotteries well, not only in Western countries, but across many different cultures. The study also found cultural and economic factors influencing systematically average prospect theory parameters.

A study published in '' Nature Human Behaviour'' in 2020 replicated research on prospect theory and concluded that it successfully replicated: "We conclude that the empirical foundations for prospect theory replicate beyond any reasonable thresholds."

Critiques

Although Prospect Theory is a largely celebrated idea in behavioural economics it does have limitations. The reference point has been argued to be difficult to precisely determine in any given context. Many external factors can influence what the reference point is and thus makes it difficult to define what a “gain” and a “loss” actually is. Kőszegi and Rabin (2007) present the idea of a personal equilibrium in decision making. This is essentially the premise that expectations and context have a large impact on determining the reference point and therefore the perception of “gains” and “losses”. Considering personal equilibrium and choice with risk creates even more ambiguity about the perception of what the reference point may be.

Some critics have charged that while prospect theory seeks to predict what people choose, it does not adequately describe the actual process of decision-making. For example, Nathan Berg and Gerd Gigerenzer claim that neither classical economics nor prospect theory provide a convincing explanation of how people actually make decisions. They go so far as to claim that prospect theory is even more demanding of cognitive resources than classical expected utility theory.

Moreover, scholars have raised doubts about the degree to which framing effects matter. For instance, John List argues that framing effects diminish in complex decision environments. His experimental evidence suggests that as actors gain experience with the consequences of competitive markets, they behave more like rational actors and the impact of prospect theory diminishes.

Steven Kachelmeier and Mohamed Shehata find little support for prospect theory among experimental subjects in China. They do not, however, make a cultural argument against prospect theory. Rather, they conclude that when payoffs are large relative to net wealth, the effect of prospect theory diminishes.Kachelmeier, Steven J., and Mohamed Shehata (1992). “Examining Risk Preferences under High Monetary Incentives: Experimental Evidence from the People’s Republic of China.” ''American Economic Review'' 82 (5): 1120–1141.

See also

Notes

Further reading

*
*
* Easterlin, Richard A.br>"Does Economic Growth Improve the Human Lot?"
in
*
*
*
* Kahneman, Daniel, Jack L. Knetsch, and Richard H. Thaler (1991). “Anomalies: The Endowment Effect, Loss Aversion, and Status Quo Bias.” ''Journal of Economic Perspectives'' 5 (1): 193–206.
* Kahneman, Daniel, and Amos Tversky, eds. (2000). ''Choices, Values, and Frames''. Cambridge: Cambridge University Press.
*
*
*
* Quattrone, George A., and Amos Tversky (1988). “Contrasting Rational and Psychological Analyses of Political Choice.” ''American Political Science Review'' 82 (3): 719–736.
*
*
*

External links

An introduction to Prospect Theory

Prospect Theory

{{DEFAULTSORT:Prospect Theory

Behavioral finance
Behavioral economics
Decision theory
Finance theories
1979 introductions
Framing (social sciences)
1979 in economic history