geometry Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...

, a Petrie polygon for a

regular polytope In mathematics, a regular polytope is a polytope whose symmetry group acts transitive group action, transitively on its flag (geometry), flags, thus giving it the highest degree of symmetry. In particular, all its elements or -faces (for all , w ...

of dimensions is a

skew polygon In geometry, a skew polygon is a closed polygonal chain in Euclidean space. It is a figure (geometry), figure similar to a polygon except its Vertex (geometry), vertices are not all coplanarity, coplanar. While a polygon is ordinarily defined a ...

in which every consecutive sides (but no ) belongs to one of the

facet Facets () are flat faces on geometric shapes. The organization of naturally occurring facets was key to early developments in crystallography, since they reflect the underlying symmetry of the crystal structure. Gemstones commonly have facets cu ...

s. The Petrie polygon of a

regular polygon In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...

is the regular polygon itself; that of a

regular polyhedron A regular polyhedron is a polyhedron whose symmetry group acts transitive group action, transitively on its Flag (geometry), flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In ...

is a skew polygon such that every two consecutive sides (but no three) belongs to one of the

face The face is the front of the head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affect th ...

s. Petrie polygons are named for mathematician John Flinders Petrie. For every regular polytope there exists an orthogonal projection onto a plane such that one Petrie polygon becomes a regular polygon with the remainder of the projection interior to it. The plane in question is the Coxeter plane of the

symmetry group In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...

of the polygon, and the number of sides, , is the Coxeter number of the

Coxeter group In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean ref ...

. These polygons and projected graphs are useful in visualizing symmetric structure of the higher-dimensional regular polytopes. Petrie polygons can be defined more generally for any embedded graph. They form the faces of another embedding of the same graph, usually on a different surface, called the Petrie dual.

History

John Flinders Petrie (1907–1972) was the son of

Egyptologist Egyptology (from ''Egypt'' and Greek , ''-logia''; ) is the scientific study of ancient Egypt. The topics studied include ancient Egyptian history, language, literature, religion, architecture and art from the 5th millennium BC until the end ...

s Hilda and Flinders Petrie. He was born in 1907 and as a schoolboy showed remarkable promise of mathematical ability. In periods of intense concentration he could answer questions about complicated four-dimensional objects by ''visualizing'' them. He first noted the importance of the regular skew polygons which appear on the surface of regular polyhedra and higher polytopes. Coxeter explained in 1937 how he and Petrie began to expand the classical subject of regular polyhedra: :One day in 1926, J. F. Petrie told me with much excitement that he had discovered two new regular polyhedral; infinite but free of false vertices. When my incredulity had begun to subside, he described them to me: one consisting of squares, six at each vertex, and one consisting of hexagons, four at each vertex. In 1938 Petrie collaborated with Coxeter, Patrick du Val, and H. T. Flather to produce '' The Fifty-Nine Icosahedra'' for publication.H. S. M. Coxeter, Patrick du Val, H. T. Flather, J. F. Petrie (1938) ''The Fifty-nine Icosahedra'',

University of Toronto The University of Toronto (UToronto or U of T) is a public university, public research university whose main campus is located on the grounds that surround Queen's Park (Toronto), Queen's Park in Toronto, Ontario, Canada. It was founded by ...

studies, mathematical series 6: 1–26 Realizing the geometric facility of the skew polygons used by Petrie, Coxeter named them after his friend when he wrote ''

Regular Polytopes ''Regular Polytopes'' is a geometry book on regular polytopes written by Harold Scott MacDonald Coxeter. It was originally published by Methuen in 1947 and by Pitman Publishing in 1948, with a second edition published by Macmillan in 1963 and a th ...

''. The idea of Petrie polygons was later extended to

semiregular polytope In geometry, by Thorold Gosset's definition a semiregular polytope is usually taken to be a polytope that is vertex-transitive and has all its facets being regular polytopes. E.L. Elte compiled a longer list in 1912 as ''The Semiregular Polyto ...

The Petrie polygons of the regular polyhedra

The regular duals, and , are contained within the same projected Petrie polygon. In the images of dual compounds on the right it can be seen that their Petrie polygons have rectangular intersections in the points where the edges touch the common

midsphere In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every Edge (geometry), edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedron, uniform polyhedra, including the reg ...

. The Petrie polygons of the Kepler–Poinsot polyhedra are

hexagon In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. Regular hexagon A regular hexagon is de ...

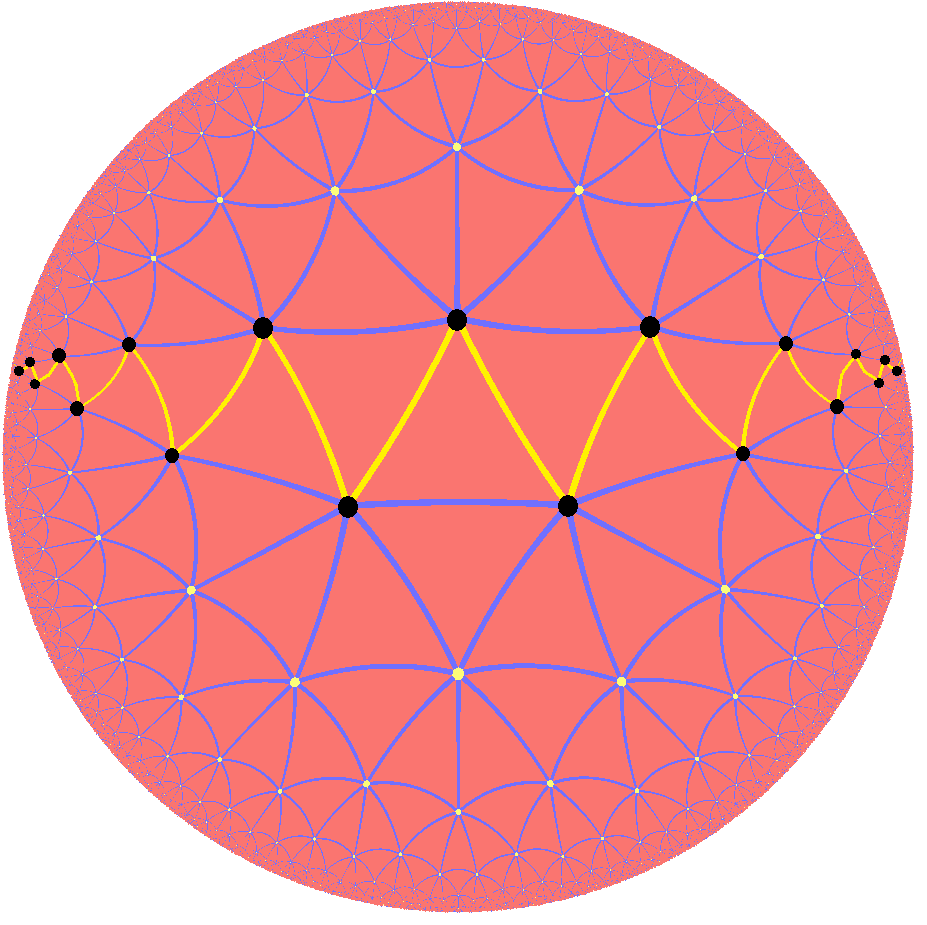
s and decagrams . Infinite regular skew polygons ( apeirogon) can also be defined as being the Petrie polygons of the regular tilings, having angles of 90, 120, and 60 degrees of their square, hexagon and triangular faces respectively. : Infinite regular skew polygons also exist as Petrie polygons of the regular hyperbolic tilings, like the order-7 triangular tiling, : : Order-7 triangular tiling petrie polygon

Order-7 triangular tiling petrie polygon

The Petrie polygon of regular polychora (4-polytopes)

The Petrie polygon for the regular polychora can also be determined, such that every three consecutive sides (but no four) belong to one of the polychoron's cells. As the surface of a 4-polytope is a 3-dimensional space (the

3-sphere In mathematics, a hypersphere or 3-sphere is a 4-dimensional analogue of a sphere, and is the 3-dimensional n-sphere, ''n''-sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. The interior o ...

), the Petrie polygon of a regular 4-polytope is a 3-dimensional helix in this surface.

The Petrie polygon projections of regular and uniform polytopes

The Petrie polygon projections are useful for the visualization of polytopes of dimension four and higher.

Hypercubes

hypercube In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...

of dimension ''n'' has a Petrie polygon of size 2''n'', which is also the number of its facets.
So each of the (''n'' − 1)-cubes forming its

surface A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...

has ''n'' − 1 sides of the Petrie polygon among its edges.

Notes

References

* Coxeter, H. S. M. (1947, 63, 73) ''Regular Polytopes'', 3rd ed. New York: Dover, 1973. (sec 2.6 ''Petrie Polygons'' pp. 24–25, and Chapter 12, pp. 213–235, ''The generalized Petrie polygon '') * Coxeter, H.S.M. (1974) ''Regular complex polytopes''. Section 4.3 Flags and Orthoschemes, Section 11.3 Petrie polygons * Ball, W. W. R. and H. S. M. Coxeter (1987) ''Mathematical Recreations and Essays'', 13th ed. New York: Dover. (p. 135) * Coxeter, H. S. M. (1999) ''The Beauty of Geometry: Twelve Essays'', Dover Publications *

Peter McMullen Peter McMullen (born 11 May 1942) is a British mathematician, a professor emeritus of mathematics at University College London. Education and career McMullen earned bachelor's and master's degrees from Trinity College, Cambridge, and studied at ...

, Egon Schulte (2002) ''Abstract Regular Polytopes'',

Cambridge University Press Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessme ...

. * Steinberg, Robert,''ON THE NUMBER OF SIDES OF A PETRIE POLYGON'', 201

External links

* * * * * * * {{DEFAULTSORT:Petrie Polygon Polytopes