|
John Flinders Petrie
John Flinders Petrie (26 April 1907 – 1972) was an English mathematician. Petrie was the great grandson of the explorer and navigator, Matthew Flinders. He met the geometer Harold Scott MacDonald Coxeter as a student, beginning a lifelong friendship. They collaborated in discovering infinite warped polyhedra and (finite) warped polyhedra in the fourth dimension, analogous to the previous ones. In addition to being the first to realize the importance of the warped polygon that now bears his name, he was also skilled as a draftsperson. Biography Petrie was born on 26 April 1907, in Hampstead, London. He was the only son of the renowned Egyptologists Sir William Matthew Flinders Petrie (and through him the great grandson of the explorer and navigator Matthew Flinders) and Hilda Petrie. While studying at a boarding school, he met Coxeter in a sanatorium while recovering from a minor illness, beginning a friendship that would remain throughout their lives.A large part of what is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
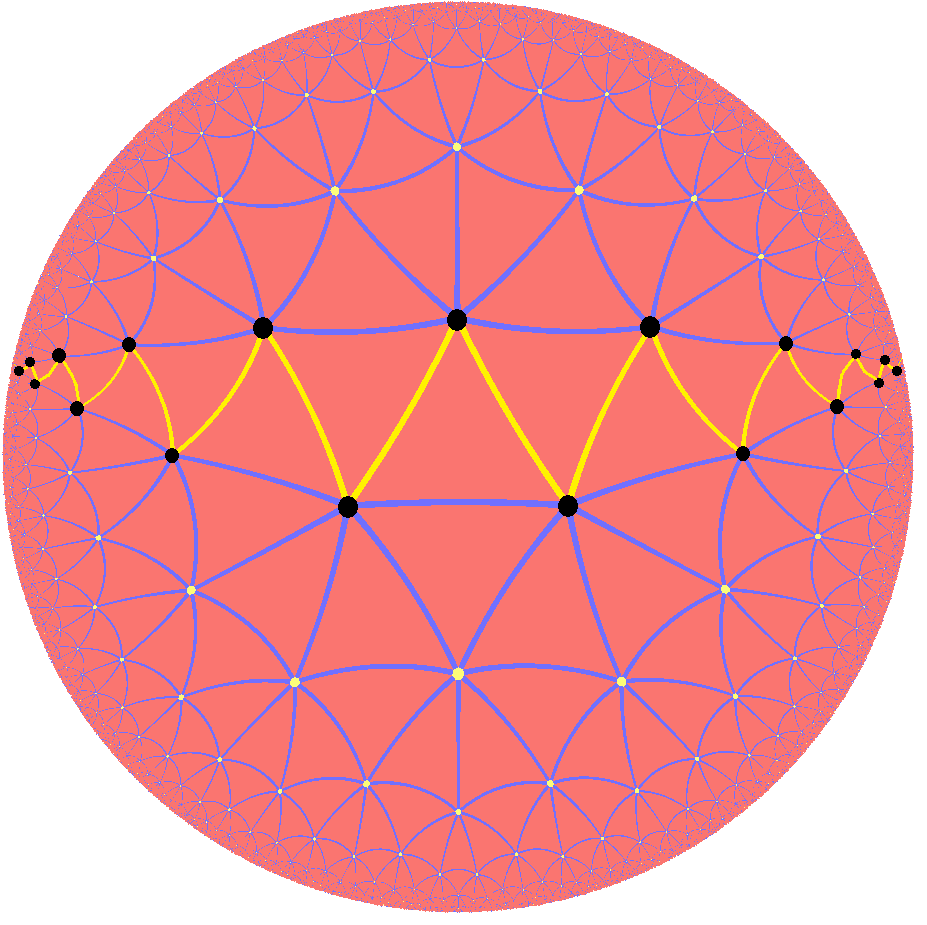
Petrie Polygon
In geometry, a Petrie polygon for a regular polytope of dimensions is a skew polygon in which every consecutive sides (but no ) belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides (but no three) belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie. For every regular polytope there exists an orthogonal projection onto a plane such that one Petrie polygon becomes a regular polygon with the remainder of the projection interior to it. The plane in question is the Coxeter plane of the symmetry group of the polygon, and the number of sides, , is the Coxeter number of the Coxeter group. These polygons and projected graphs are useful in visualizing symmetric structure of the higher-dimensional regular polytopes. Petrie polygons can be defined more generally for any embedded graph. They form the faces of ano ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Polygon
In geometry, a skew polygon is a closed polygonal chain in Euclidean space. It is a figure (geometry), figure similar to a polygon except its Vertex (geometry), vertices are not all coplanarity, coplanar. While a polygon is ordinarily defined as a plane figure, the edge (geometry), edges and vertices of a skew polygon form a space curve. Skew polygons must have at least four vertices. The ''interior'' surface (geometry), surface and corresponding area measure of such a polygon is not uniquely defined. Skew infinite polygons (apeirogons) have vertices which are not all colinear. A zig-zag skew polygon or antiprismatic polygonRegular complex polytopes, p. 6 has vertices which alternate on two parallel planes, and thus must be even-sided. Regular skew polygons in 3 dimensions (and regular skew apeirogons in two dimensions) are always zig-zag. Skew polygons in three dimensions A regular skew polygon is a faithful symmetric realization of a polygon in dimension greater than 2. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometers
A geometer is a mathematician whose area of study is the historical aspects that define geometry, instead of the analytical geometric studies that becomes conducted from geometricians. Some notable geometers and their main fields of work, chronologically listed, are: 1000 BCE to 1 BCE * Baudhayana (fl. c. 800 BC) – Euclidean geometry * Manava (c. 750 BC–690 BC) – Euclidean geometry * Thales of Miletus (c. 624 BC – c. 546 BC) – Euclidean geometry * Pythagoras (c. 570 BC – c. 495 BC) – Euclidean geometry, Pythagorean theorem * Zeno of Elea (c. 490 BC – c. 430 BC) – Euclidean geometry * Hippocrates of Chios (born c. 470 – 410 BC) – first systematically organized '' Stoicheia – Elements'' (geometry textbook) * Mozi (c. 468 BC – c. 391 BC) * Plato (427–347 BC) * Theaetetus (c. 417 BC – 369 BC) * Autolycus of Pitane (360–c. 290 BC) – astronomy, spherical geometry * Euclid (fl. 300 BC) – '' Elements'', Euclidean geometry (sometimes called t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polytopes
In elementary geometry, a polytope is a geometric object with Flat (geometry), flat sides (''Face (geometry), faces''). Polytopes are the generalization of three-dimensional polyhedron, polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -dimensional polytope or -polytope. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope. In this context, "flat sides" means that the sides of a -polytope consist of -polytopes that may have -polytopes in common. Some theories further generalize the idea to include such objects as unbounded apeirotopes and tessellations, decompositions or tilings of curved manifolds including spherical polyhedra, and set-theoretic abstract polytopes. Polytopes of more than three dimensions were first discovered by Ludwig Schläfli before 1853, who called such a figure a polyschem. The German language, German term ''Polytop'' was coined by the mathematician Re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Road Incident Deaths In The United Kingdom
A road is a thoroughfare used primarily for movement of traffic. Roads differ from streets, whose primary use is local access. They also differ from stroads, which combine the features of streets and roads. Most modern roads are Road surface, paved. The words "road" and "street" are commonly considered to be interchangeable, but the distinction is important in urban design. There are road hierarchy, many types of roads, including parkways, avenue (landscape), avenues, controlled-access highways (freeways, motorways, and expressways), tollways, interstates, highways, and local roads. The primary features of roads include lanes, sidewalks (pavement), roadways (carriageways), median strip, medians, shoulder (road), shoulders, road verge, verges, bike paths (cycle paths), and shared-use paths. Definitions Historically, many roads were simply recognizable routes without any formal construction or some maintenance. The Organisation for Economic Co-operation and Development, Organi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Polygon
In geometry, a skew polygon is a closed polygonal chain in Euclidean space. It is a figure (geometry), figure similar to a polygon except its Vertex (geometry), vertices are not all coplanarity, coplanar. While a polygon is ordinarily defined as a plane figure, the edge (geometry), edges and vertices of a skew polygon form a space curve. Skew polygons must have at least four vertices. The ''interior'' surface (geometry), surface and corresponding area measure of such a polygon is not uniquely defined. Skew infinite polygons (apeirogons) have vertices which are not all colinear. A zig-zag skew polygon or antiprismatic polygonRegular complex polytopes, p. 6 has vertices which alternate on two parallel planes, and thus must be even-sided. Regular skew polygons in 3 dimensions (and regular skew apeirogons in two dimensions) are always zig-zag. Skew polygons in three dimensions A regular skew polygon is a faithful symmetric realization of a polygon in dimension greater than 2. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Discussion Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry are the natural analog of straight lines in Euclidean space. For any pair of distinct non- antipodal points on the sphere, there is a unique great circle passing through both. (Every great circle through any point also passes through its antipodal point, so there are infinitely many great circles through two antipodal points.) The shorter of the two great-circle arcs between two distinct points on the sphere is called the ''minor arc'', and is the shortest surface-path between them. Its arc length is the great-circle distance between the points (the intrinsic distance on a sphere), and is proportional to the measure of the central angle formed by the two points and the center of the sphere. A great circle is the largest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polyhedron
A regular polyhedron is a polyhedron whose symmetry group acts transitive group action, transitively on its Flag (geometry), flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are Congruence (geometry), congruent regular polygons which are assembled in the same way around each vertex (geometry), vertex. A regular polyhedron is identified by its Schläfli symbol of the form , where ''n'' is the number of sides of each face and ''m'' the number of faces meeting at each vertex. There are 5 finite convex regular polyhedra (the Platonic solids), and four regular star polyhedra (the Kepler–Poinsot polyhedra), making nine regular polyhedra in all. In addition, there are five regular compounds of the regular polyhedra. The regular polyhedra There are five Convex polygon, convex regular polyhedra, known as the Platoni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harold Coxeter
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century. Coxeter was born in England and educated at the University of Cambridge, with student visits to Princeton University. He worked for 60 years at the University of Toronto in Canada, from 1936 until his retirement in 1996, becoming a full professor there in 1948. His many honours included membership in the Royal Society of Canada, the Royal Society, and the Order of Canada. He was an author of 12 books, including ''The Fifty-Nine Icosahedra'' (1938) and ''Regular Polytopes'' (1947). Many concepts in geometry and group theory are named after him, including the Coxeter graph, Coxeter groups, Coxeter's loxodromic sequence of tangent circles, Coxeter–Dynkin diagrams, and the Todd–Coxeter algorithm. Biography Coxeter was born in Kensington, England, to Harold Samuel Coxeter and L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second World War
World War II or the Second World War (1 September 1939 – 2 September 1945) was a World war, global conflict between two coalitions: the Allies of World War II, Allies and the Axis powers. World War II by country, Nearly all of the world's countries participated, with many nations mobilising all resources in pursuit of total war. Tanks in World War II, Tanks and Air warfare of World War II, aircraft played major roles, enabling the strategic bombing of cities and delivery of the Atomic bombings of Hiroshima and Nagasaki, first and only nuclear weapons ever used in war. World War II is the List of wars by death toll, deadliest conflict in history, causing World War II casualties, the death of 70 to 85 million people, more than half of whom were civilians. Millions died in genocides, including the Holocaust, and by massacres, starvation, and disease. After the Allied victory, Allied-occupied Germany, Germany, Allied-occupied Austria, Austria, Occupation of Japan, Japan, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |