Pentagonal Truncated Trapezohedron

In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular:
The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry.

The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. There are numerous other dodecahedra.

While the regular dodecahedron shares many features with other Platonic solids, one unique property of it is that one can start at a corner of the surface and draw an infinite number of straight lines across the figure that return to the original point without crossing over any other corner.

Regular dodecahedron

The convex regular dodecahedron is one of the five regular Platonic solids and can be represented by its Schläfli symbol .

The dual polyhedron is the regular icosahedron , having five equilateral triangles around each vertex.

The convex regular dodecahedron also has three stellations, all of which are regular star dodecahedra. They form three of the four Kepler–Poinsot polyhedra. They are the small stellated dodecahedron , the great dodecahedron , and the great stellated dodecahedron . The small stellated dodecahedron and great dodecahedron are dual to each other; the great stellated dodecahedron is dual to the great icosahedron . All of these regular star dodecahedra have regular pentagonal or pentagrammic faces. The convex regular dodecahedron and great stellated dodecahedron are different realisations of the same abstract regular polyhedron; the small stellated dodecahedron and great dodecahedron are different realisations of another abstract regular polyhedron.

Other pentagonal dodecahedra

In crystallography, two important dodecahedra can occur as crystal forms in some symmetry classes of the cubic crystal system that are topologically equivalent to the regular dodecahedron but less symmetrical: the pyritohedron with pyritohedral symmetry, and the tetartoid with tetrahedral symmetry:

Pyritohedron

A pyritohedron is a dodecahedron with pyritohedral (T_h) symmetry. Like the regular dodecahedron, it has twelve identical pentagonal faces, with three meeting in each of the 20 vertices (see figure). However, the pentagons are not constrained to be regular, and the underlying atomic arrangement has no true fivefold symmetry axis. Its 30 edges are divided into two sets – containing 24 and 6 edges of the same length. The only axes of rotational symmetry are three mutually perpendicular twofold axes and four threefold axes.

Although regular dodecahedra do not exist in crystals, the pyritohedron form occurs in the crystals of the mineral pyrite, and it may be an inspiration for the discovery of the regular Platonic solid form. The true regular dodecahedron can occur as a shape for quasicrystals (such as holmium–magnesium–zinc quasicrystal) with icosahedral symmetry, which includes true fivefold rotation axes.

Crystal pyrite

The name ''crystal pyrite'' comes from one of the two common crystal habits shown by pyrite (the other one being the cube). In pyritohedral pyrite, the faces have a Miller index of (210), which means that the dihedral angle is 2·arctan(2) ≈ 126.87° and each pentagonal face has one angle of approximately 121.6° in between two angles of approximately 106.6° and opposite two angles of approximately 102.6°. The following formulas show the measurements for the face of a perfect crystal (which is rarely found in nature).

$\text = \frac \cdot \text$

$\text = \frac \cdot \text$

$\text = \sqrt \cdot \text$

Cartesian coordinates

The eight vertices of a cube have the coordinates (±1, ±1, ±1).

The coordinates of the 12 additional vertices are
(0, ±(1 + ''h''), ±(1 − ''h''²)),
(±(1 + ''h''), ±(1 − ''h''²), 0) and
(±(1 − ''h''²), 0, ±(1 + ''h'')).

''h'' is the height of the wedge-shaped "roof" above the faces of that cube with edge length 2.

An important case is ''h'' = (a quarter of the cube edge length) for perfect natural pyrite (also the pyritohedron in the Weaire–Phelan structure).

Another one is ''h'' = = 0.618... for the regular dodecahedron. See section '' Geometric freedom'' for other cases.

Two pyritohedra with swapped nonzero coordinates are in dual positions to each other like the dodecahedra in the compound of two dodecahedra.

Geometric freedom

The pyritohedron has a geometric degree of freedom with limiting cases of a cubic convex hull at one limit of collinear edges, and a rhombic dodecahedron as the other limit as 6 edges are degenerated to length zero. The regular dodecahedron represents a special intermediate case where all edges and angles are equal.

It is possible to go past these limiting cases, creating concave or nonconvex pyritohedra. The ''endo-dodecahedron'' is concave and equilateral; it can tessellate space with the convex regular dodecahedron. Continuing from there in that direction, we pass through a degenerate case where twelve vertices coincide in the centre, and on to the regular great stellated dodecahedron where all edges and angles are equal again, and the faces have been distorted into regular pentagrams. On the other side, past the rhombic dodecahedron, we get a nonconvex equilateral dodecahedron with fish-shaped self-intersecting equilateral pentagonal faces.

Tetartoid

A tetartoid (also tetragonal pentagonal dodecahedron, pentagon-tritetrahedron, and tetrahedric pentagon dodecahedron) is a dodecahedron with chiral tetrahedral symmetry (T). Like the regular dodecahedron, it has twelve identical pentagonal faces, with three meeting in each of the 20 vertices. However, the pentagons are not regular and the figure has no fivefold symmetry axes.

Although regular dodecahedra do not exist in crystals, the tetartoid form does. The name tetartoid comes from the Greek root for one-fourth because it has one fourth of full octahedral symmetry, and half of pyritohedral symmetry. The mineral cobaltite can have this symmetry form.

Abstractions sharing the solid's topology and symmetry can be created from the cube and the tetrahedron. In the cube each face is bisected by a slanted edge. In the tetrahedron each edge is trisected, and each of the new vertices connected to a face center. (In Conway polyhedron notation this is a gyro tetrahedron.)

Cartesian coordinates

The following points are vertices of a tetartoid pentagon under tetrahedral symmetry:
:(''a'', ''b'', ''c''); (−''a'', −''b'', ''c''); (−, −, ); (−''c'', −''a'', ''b''); (−, , ),
under the following conditions:
:,
:''n'' = ''a''²''c'' − ''bc''²,
:''d''₁ = ''a''² − ''ab'' + ''b''² + ''ac'' − 2''bc'',
:''d''₂ = ''a''² + ''ab'' + ''b''² − ''ac'' − 2''bc'',
:.

Geometric freedom

The regular dodecahedron is a tetartoid with more than the required symmetry. The triakis tetrahedron is a degenerate case with 12 zero-length edges. (In terms of the colors used above this means, that the white vertices and green edges are absorbed by the green vertices.)

Dual of triangular gyrobianticupola

A lower symmetry form of the regular dodecahedron can be constructed as the dual of a polyhedron constructed from two triangular anticupola connected base-to-base, called a ''triangular gyrobianticupola.'' It has D_3d symmetry, order 12. It has 2 sets of 3 identical pentagons on the top and bottom, connected 6 pentagons around the sides which alternate upwards and downwards. This form has a hexagonal cross-section and identical copies can be connected as a partial hexagonal honeycomb, but all vertices will not match.
:

Rhombic dodecahedron

The '' rhombic dodecahedron'' is a zonohedron with twelve rhombic faces and octahedral symmetry. It is dual to the quasiregular cuboctahedron (an Archimedean solid) and occurs in nature as a crystal form. The rhombic dodecahedron packs together to fill space.

The ''rhombic dodecahedron'' can be seen as a degenerate pyritohedron where the 6 special edges have been reduced to zero length, reducing the pentagons into rhombic faces.

The rhombic dodecahedron has several stellations, the first of which is also a parallelohedral spacefiller.

Another important rhombic dodecahedron, the Bilinski dodecahedron, has twelve faces congruent to those of the rhombic triacontahedron, i.e. the diagonals are in the ratio of the golden ratio. It is also a zonohedron and was described by Bilinski in 1960. This figure is another spacefiller, and can also occur in non-periodic spacefillings along with the rhombic triacontahedron, the rhombic icosahedron and rhombic hexahedra.

Other dodecahedra

There are 6,384,634 topologically distinct ''convex'' dodecahedra, excluding mirror images—the number of vertices ranges from 8 to 20.Counting polyhedra
Numericana.com (2001-12-31). Retrieved on 2016-12-02. (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.)

Topologically distinct dodecahedra (excluding pentagonal and rhombic forms)
*Uniform polyhedra:
** Decagonal prism – 10 squares, 2 decagons, D_10h symmetry, order 40.
** Pentagonal antiprism – 10 equilateral triangles, 2 pentagons, D_5d symmetry, order 20
*Johnson solids (regular faced):
** Pentagonal cupola – 5 triangles, 5 squares, 1 pentagon, 1 decagon, C_5v symmetry, order 10
** Snub disphenoid – 12 triangles, D_2d, order 8
** Elongated square dipyramid – 8 triangles and 4 squares, D_4h symmetry, order 16
** Metabidiminished icosahedron – 10 triangles and 2 pentagons, C_2v symmetry, order 4
*Congruent irregular faced: ( face-transitive)
** Hexagonal bipyramid – 12 isosceles triangles, dual of hexagonal prism, D_6h symmetry, order 24
** Hexagonal trapezohedron – 12 kites, dual of hexagonal antiprism, D_6d symmetry, order 24
** Triakis tetrahedron – 12 isosceles triangles, dual of truncated tetrahedron, T_d symmetry, order 24
*Other less regular faced:
**Hendecagonal pyramid – 11 isosceles triangles and 1 regular hendecagon, C_11v, order 11
** Trapezo-rhombic dodecahedron – 6 rhombi, 6 trapezoids – dual of triangular orthobicupola, D_3h symmetry, order 12
** Rhombo-hexagonal dodecahedron or ''elongated Dodecahedron'' – 8 rhombi and 4 equilateral hexagons, D_4h symmetry, order 16
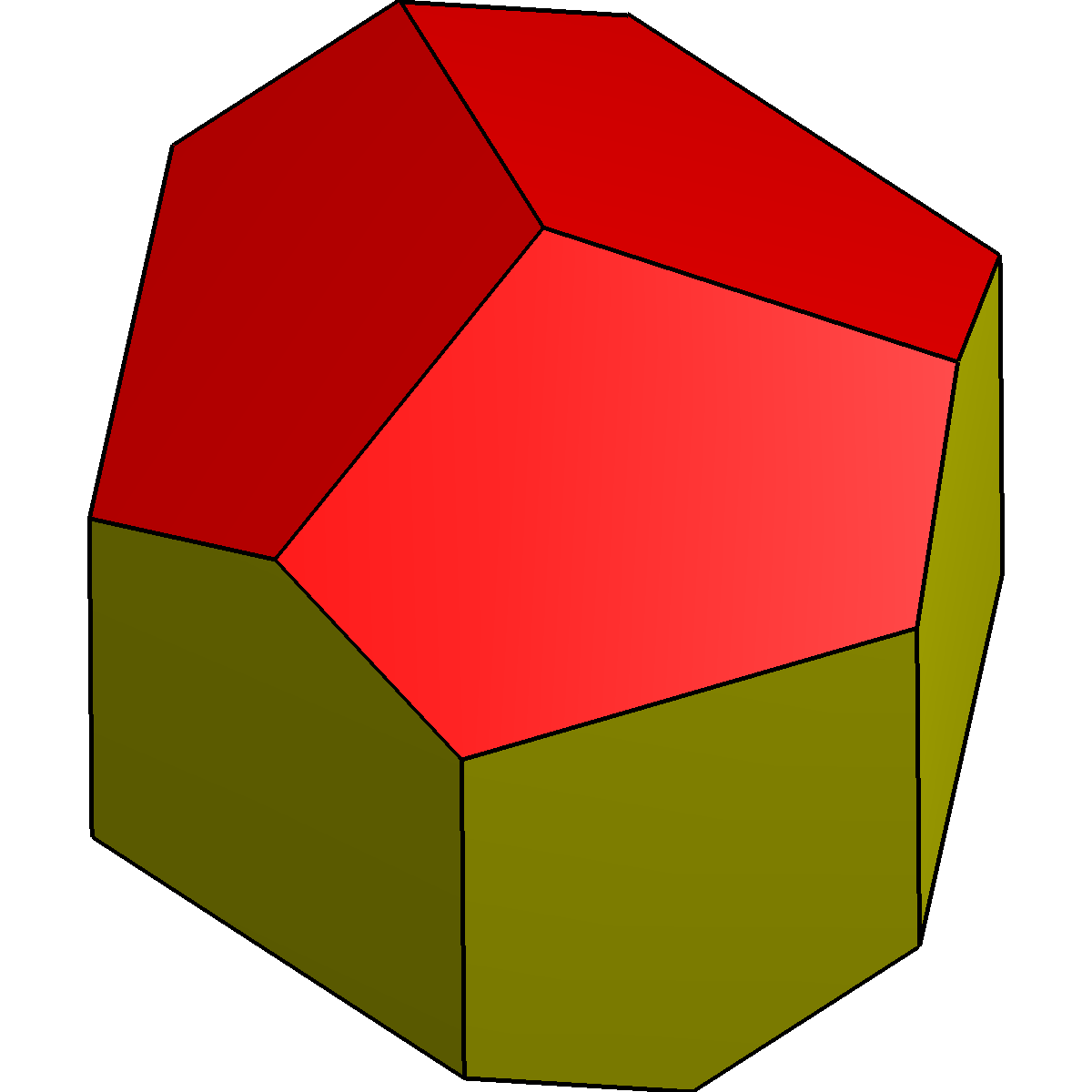
** Truncated pentagonal trapezohedron, D_5d, order 20, topologically equivalent to regular dodecahedron

Practical usage

Armand Spitz used a dodecahedron as the "globe" equivalent for his Digital Dome planetarium projector. based upon a suggestion from Albert Einstein.

See also

* 120-cell – a regular polychoron (4D polytope) whose surface consists of 120 dodecahedral cells
* – a dodecahedron shaped coccolithophore (a unicellular phytoplankton algae)
* Pentakis dodecahedron
* Roman dodecahedron
* Snub dodecahedron
* Truncated dodecahedron

References

External links

*''Plato's Fourth Solid and the "Pyritohedron"'', by Paul Stephenson, 1993, The Mathematical Gazette, Vol. 77, No. 479 (Jul., 1993), pp. 220–22
Stellation of Pyritohedron
VRML models and animations of Pyritohedron and its stellations
*
Editable printable net of a dodecahedron with interactive 3D viewThe Uniform PolyhedraOrigami Polyhedra
– Models made with Modular Origami

The Encyclopedia of Polyhedra

*[http://www.bodurov.com/VectorVisualizer/?vectors=-0.94/-2.885/-3.975/-1.52/-4.67/-0.94v-3.035/0/-3.975/-4.91/0/-0.94v3.975/-2.885/-0.94/1.52/-4.67/0.94v1.52/-4.67/0.94/-1.52/-4.67/-0.94v0.94/-2.885/3.975/1.52/-4.67/0.94v-3.975/-2.885/0.94/-1.52/-4.67/-0.94v-3.975/-2.885/0.94/-4.91/0/-0.94v-3.975/2.885/0.94/-4.91/0/-0.94v-3.975/2.885/0.94/-1.52/4.67/-0.94v-2.455/1.785/3.975/-3.975/2.885/0.94v-2.455/-1.785/3.975/-3.975/-2.885/0.94v-1.52/4.67/-0.94/-0.94/2.885/-3.975v4.91/0/0.94/3.975/-2.885/-0.94v3.975/2.885/-0.94/2.455/1.785/-3.975v2.455/-1.785/-3.975/3.975/-2.885/-0.94v1.52/4.67/0.94/-1.52/4.67/-0.94v3.035/0/3.975/0.94/2.885/3.975v0.94/2.885/3.975/-2.455/1.785/3.975v-2.455/1.785/3.975/-2.455/-1.785/3.975v-2.455/-1.785/3.975/0.94/-2.885/3.975v0.94/-2.885/3.975/3.035/0/3.975v2.455/1.785/-3.975/-0.94/2.885/-3.975v-0.94/2.885/-3.975/-3.035/0/-3.975v-3.035/0/-3.975/-0.94/-2.885/-3.975v-0.94/-2.885/-3.975/2.455/-1.785/-3.975v2.455/-1.785/-3.975/2.455/1.785/-3.97v3.035/0/3.975/4.91/0/0.94v4.91/0/0.94/3.975/2.885/-0.94v3.975/2.885/-0.94/1.52/4.67/0.94v1.52/4.67/0.94/0.94/2.885/3.975 Dodecahedron 3D Visualization]
Stella: Polyhedron Navigator
Software used to create some of the images on this page.
How to make a dodecahedron from a Styrofoam cube

{{Authority control

Individual graphs
Planar graphs
Platonic solids
12 (number)