|
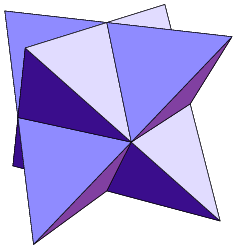
Snub Disphenoid
In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its face (geometry), faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape is also called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron. The snub disphenoid can be visualized as an atom cluster surrounding a central atom, that is the dodecahedral molecular geometry. Its vertices may be placed in a sphere and can also be used as a minimum possible Lennard-Jones potential among all eight-sphere clusters. The dual polyhedron of the snub disphenoid is the elongated gyrobifastigium. Construction The snub disphenoid can be constructed in different ways. As suggested by the name, the snub disphenoid is constructed from a tetragonal disphenoid by cutting all the edges from its faces, and adding equilateral triangles (the light blue colors in the following image) that are twisted in a certain a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Gyrobifastigium
In geometry, the elongated gyrobifastigium or gabled rhombohedron is a space-filling octahedron with 4 rectangles and 4 right-angled pentagonal faces. Name The first name is from the regular-faced gyrobifastigium but Elongation (geometry), elongated with 4 triangles expanded into pentagons. The name of the gyrobifastigium comes from the Latin ''fastigium'', meaning a sloping roof. In the standard naming convention of the Johnson solids, ''bi-'' means two solids connected at their bases, and ''gyro-'' means the two halves are twisted with respect to each other. The gyrobifastigium is first in a series of gyrobicupola, so this solid can also be called an ''elongated digonal gyrobicupola''. Geometrically it can also be constructed as the dual of a digonal gyrobianticupola. This construction is space-filling. The second name, ''gabled rhombohedron'', is from Michael Goldberg's paper on space-filling octahedra, model 8-VI, the 6th of at least 49 space-filling octahedra. A gable is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deltahedron
A deltahedron is a polyhedron whose faces are all equilateral triangles. The deltahedron was named by Martyn Cundy, after the Greek capital letter delta resembling a triangular shape Δ. Deltahedra can be categorized by the property of convexity. The simplest convex deltahedron is the regular tetrahedron, a pyramid with four equilateral triangles. There are eight convex deltahedra, which can be used in the applications of chemistry as in the polyhedral skeletal electron pair theory and chemical compounds. There are infinitely many concave deltahedra. Strictly convex deltahedron A polyhedron is said to be ''convex'' if a line between any two of its vertices lies either within its interior or on its boundary, and additionally, if no two faces are coplanar (lying in the same plane) and no two edges are collinear (segments of the same line), it can be considered as being strictly convex. Of the eight convex deltahedra, three are Platonic solids and five are Johnson solids. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Bipyramid
The pentagonal bipyramid (or pentagonal dipyramid) is a polyhedron with ten triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an example of deltahedra, composite polyhedron, and Johnson solid. The pentagonal bipyramid may be represented as four-connected well-covered graph. This polyhedron may be used in the chemical compound as the description of an atom cluster known as pentagonal bipyramidal molecular geometry, as a solution in Thomson problem, as well as in decahedral nanoparticles. Special cases As a right bipyramid Like other bipyramids, the pentagonal bipyramid can be constructed by attaching the base of two pentagonal pyramids. These pyramids cover their pentagonal base, such that the resulting polyhedron has ten triangles as its faces, fifteen edges, and seven vertices. The pentagonal bipyramid is said to be right if the pyramids are symmetri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a set of points is convex if it contains every line segment between two points in the set. For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary (topology), boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval (mathematics), interval with the property that its epigraph (mathematics), epigraph (the set of points on or above the graph of a function, graph of the function) is a convex set. Convex minimization is a subfield of mathematical optimization, optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compass-and-straightedge Construction
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a compass. The idealized ruler, known as a straightedge, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so it may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really means: see Markable rulers below.) More formally, the o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Casus Irreducibilis
() is the name given by mathematicians of the 16th century to cubic equations that cannot be solved in terms of real radicals, that is to those equations such that the computation of the solutions cannot be ''reduced'' to the computation of square and cube roots. Cardano's formula for solution in radicals of a cubic equation was discovered at this time. It applies in the ''casus irreducibilis'', but, in this case, requires the computation of the square root of a negative number, which involves knowledge of complex numbers, unknown at the time. The casus irreducibilis occurs when the three solutions are real and distinct, or, equivalently, when the discriminant is positive. It is only in 1843 that Pierre Wantzel proved that there cannot exist any solution in real radicals in the ''casus irreducibilis''. The three cases of the discriminant Let : ax^3+bx^2+cx+d=0 be a cubic equation with a\ne0. Then the discriminant is given by : D := \bigl((x_1-x_2)(x_1-x_3)(x_2-x_3)\bigr)^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular oriented lines, called '' coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the '' origin'' and has as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any dimension . These coordinates are the signed distances from the point to mutually perpendicular fixed h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Origami
) is the Japanese art of paper folding. In modern usage, the word "origami" is often used as an inclusive term for all folding practices, regardless of their culture of origin. The goal is to transform a flat square sheet of paper into a finished sculpture through folding and sculpting techniques. Modern origami practitioners generally discourage the use of cuts, glue, or markings on the paper. Origami folders often use the Japanese word ' to refer to designs which use cuts. In the detailed Japanese classification, origami is divided into stylized ceremonial origami (儀礼折り紙, ''girei origami'') and recreational origami (遊戯折り紙, ''yūgi origami''), and only recreational origami is generally recognized as origami. In Japan, ceremonial origami is generally called "origata" ( :ja:折形) to distinguish it from recreational origami. The term "origata" is one of the old terms for origami. The small number of basic origami folds can be combined in a variety of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Montroll
John Montroll is an American origami artist, author, teacher, and mathematician. He has written many books on origami, promoting the single-square, no-cut, no glue approach. Montroll taught mathematics at St. Anselm's Abbey School in Washington, D.C. from 1990 to 2021. Biography John Montroll was born in Washington, D.C.The Origamian, Vol.9, Issue 3, 1970, Published by the Origami Center He is the son of Elliott Waters Montroll, an American scientist and mathematician. He has a Bachelor of Arts degree in Mathematics from the University of Rochester, a Master of Arts in Electrical Engineering from the University of Michigan, and a Master of Arts in applied mathematics from the University of Maryland. Montroll mastered his first origami book, Isao Honda's ''How to make Origami'', at the age of six, the same age he began creating his own origami animals.The Paper, Issue 55, Summer 1996, The Magazine of OrigamiUSA He became a member of the Origami Center of America at age twelve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyiamond
A polyiamond (also polyamond or simply iamond, or sometimes triangular polyomino) is a polyform whose base form is an equilateral triangle. The word ''polyiamond'' is a back-formation from ''diamond'', because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial 'di-' looks like a Greek prefix meaning 'two-' (though ''diamond'' actually derives from Greek '' ἀδάμας'' - also the basis for the word "adamant"). The name was suggested by recreational mathematics writer Thomas H. O'Beirne in ''New Scientist'' 1961 number 1, page 164. Counting The basic combinatorial question is, How many different polyiamonds exist with a given number of cells? Like polyominoes, polyiamonds may be either free or one-sided. Free polyiamonds are invariant under reflection as well as translation and rotation. One-sided polyiamonds distinguish reflections. The number of free ''n''-iamonds for ''n'' = 1, 2, 3, ... is: :1, 1, 1, 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Net (polyhedron)
In geometry, a net of a polyhedron is an arrangement of non-overlapping Edge (geometry), edge-joined polygons in the plane (geometry), plane which can be folded (along edges) to become the face (geometry), faces of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and solid geometry in general, as they allow for physical models of polyhedra to be constructed from material such as thin cardboard. An early instance of polyhedral nets appears in the works of Albrecht Dürer, whose 1525 book ''A Course in the Art of Measurement with Compass and Ruler'' (''Unterweysung der Messung mit dem Zyrkel und Rychtscheyd '') included nets for the Platonic solids and several of the Archimedean solids. These constructions were first called nets in 1543 by Augustin Hirschvogel. Existence and uniqueness Many different nets can exist for a given polyhedron, depending on the choices of which edges are joined and which are separated. The edges that are cut from a convex poly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |