Oscillation on:
[Wikipedia]
[Google]
[Amazon]
 Oscillation is the repetitive or periodic variation, typically in
Oscillation is the repetitive or periodic variation, typically in
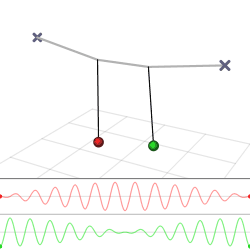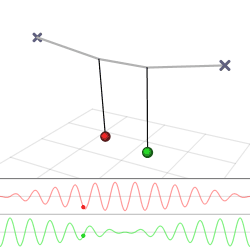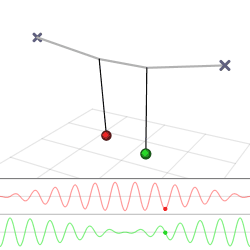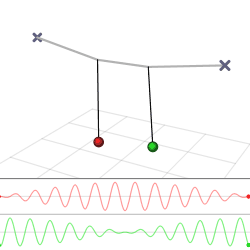 The harmonic oscillator and the systems it models have a single degree of freedom. More complicated systems have more degrees of freedom, for example, two masses and three springs (each mass being attached to fixed points and to each other). In such cases, the behavior of each variable influences that of the others. This leads to a ''coupling'' of the oscillations of the individual degrees of freedom. For example, two pendulum clocks (of identical frequency) mounted on a common wall will tend to synchronise. This
The harmonic oscillator and the systems it models have a single degree of freedom. More complicated systems have more degrees of freedom, for example, two masses and three springs (each mass being attached to fixed points and to each other). In such cases, the behavior of each variable influences that of the others. This leads to a ''coupling'' of the oscillations of the individual degrees of freedom. For example, two pendulum clocks (of identical frequency) mounted on a common wall will tend to synchronise. This
 Oscillation is the repetitive or periodic variation, typically in
Oscillation is the repetitive or periodic variation, typically in time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ...
, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum
A pendulum is a device made of a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate i ...
and alternating current
Alternating current (AC) is an electric current that periodically reverses direction and changes its magnitude continuously with time, in contrast to direct current (DC), which flows only in one direction. Alternating current is the form in w ...
. Oscillations can be used in physics to approximate complex interactions, such as those between atoms.
Oscillations occur not only in mechanical systems but also in dynamic systems in virtually every area of science: for example the beating of the human heart (for circulation), business cycle
Business cycles are intervals of general expansion followed by recession in economic performance. The changes in economic activity that characterize business cycles have important implications for the welfare of the general population, governmen ...
s in economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
, predator–prey population cycles in ecology
Ecology () is the natural science of the relationships among living organisms and their Natural environment, environment. Ecology considers organisms at the individual, population, community (ecology), community, ecosystem, and biosphere lev ...
, geothermal geysers in geology
Geology (). is a branch of natural science concerned with the Earth and other astronomical objects, the rocks of which they are composed, and the processes by which they change over time. Modern geology significantly overlaps all other Earth ...
, vibration of strings in guitar
The guitar is a stringed musical instrument that is usually fretted (with Fretless guitar, some exceptions) and typically has six or Twelve-string guitar, twelve strings. It is usually held flat against the player's body and played by strumming ...
and other string instrument
In musical instrument classification, string instruments, or chordophones, are musical instruments that produce sound from vibrating strings when a performer strums, plucks, strikes or sounds the strings in varying manners.
Musicians play some ...
s, periodic firing of nerve cells in the brain, and the periodic swelling of Cepheid variable stars in astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
. The term ''vibration
Vibration () is a mechanical phenomenon whereby oscillations occur about an equilibrium point. Vibration may be deterministic if the oscillations can be characterised precisely (e.g. the periodic motion of a pendulum), or random if the os ...
'' is precisely used to describe a mechanical oscillation.
Oscillation, especially rapid oscillation, may be an undesirable phenomenon in process control
Industrial process control (IPC) or simply process control is a system used in modern manufacturing which uses the principles of control theory and physical industrial control systems to monitor, control and optimize continuous Industrial processe ...
and control theory
Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the applic ...
(e.g. in sliding mode control), where the aim is convergence to stable state. In these cases it is called chattering or flapping, as in valve chatter, and route flapping.
Simple harmonic oscillation
The simplest mechanical oscillating system is aweight
In science and engineering, the weight of an object is a quantity associated with the gravitational force exerted on the object by other objects in its environment, although there is some variation and debate as to the exact definition.
Some sta ...
attached to a linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
spring subject to only weight
In science and engineering, the weight of an object is a quantity associated with the gravitational force exerted on the object by other objects in its environment, although there is some variation and debate as to the exact definition.
Some sta ...
and tension. Such a system may be approximated on an air table or ice surface. The system is in an equilibrium state when the spring is static. If the system is displaced from the equilibrium, there is a net ''restoring force'' on the mass, tending to bring it back to equilibrium. However, in moving the mass back to the equilibrium position, it has acquired momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
which keeps it moving beyond that position, establishing a new restoring force in the opposite sense. If a constant force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitu ...
such as gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
is added to the system, the point of equilibrium is shifted. The time taken for an oscillation to occur is often referred to as the oscillatory ''period''.
The systems where the restoring force on a body is directly proportional to its displacement, such as the dynamics of the spring-mass system, are described mathematically by the simple harmonic oscillator
In mechanics and physics, simple harmonic motion (sometimes abbreviated as ) is a special type of periodic function, periodic motion an object experiences by means of a restoring force whose magnitude is directly proportionality (mathematics), ...
and the regular periodic motion is known as simple harmonic motion. In the spring-mass system, oscillations occur because, at the static equilibrium displacement, the mass has kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
which is converted into potential energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity ...
stored in the spring at the extremes of its path. The spring-mass system illustrates some common features of oscillation, namely the existence of an equilibrium and the presence of a restoring force which grows stronger the further the system deviates from equilibrium.
In the case of the spring-mass system, Hooke's law states that the restoring force of a spring is:
By using Newton's second law, the differential equation can be derived:
where
The solution to this differential equation produces a sinusoidal position function:
where is the frequency of the oscillation, is the amplitude, and is the phase shift of the function. These are determined by the initial conditions of the system. Because cosine oscillates between 1 and −1 infinitely, our spring-mass system would oscillate between the positive and negative amplitude forever without friction.
Two-dimensional oscillators
In two or three dimensions, harmonic oscillators behave similarly to one dimension. The simplest example of this is an isotropic oscillator, where the restoring force is proportional to the displacement from equilibrium with the same restorative constant in all directions. This produces a similar solution, but now there is a different equation for every direction.Anisotropic oscillators
Withanisotropic
Anisotropy () is the structural property of non-uniformity in different directions, as opposed to isotropy. An anisotropic object or pattern has properties that differ according to direction of measurement. For example, many materials exhibit ver ...
oscillators, different directions have different constants of restoring forces. The solution is similar to isotropic oscillators, but there is a different frequency in each direction. Varying the frequencies relative to each other can produce interesting results. For example, if the frequency in one direction is twice that of another, a figure eight pattern is produced. If the ratio of frequencies is irrational, the motion is quasiperiodic. This motion is periodic on each axis, but is not periodic with respect to r, and will never repeat.
Damped oscillations
All real-world oscillator systems are thermodynamically irreversible. This means there are dissipative processes such as friction orelectrical resistance
The electrical resistance of an object is a measure of its opposition to the flow of electric current. Its reciprocal quantity is , measuring the ease with which an electric current passes. Electrical resistance shares some conceptual paral ...
which continually convert some of the energy stored in the oscillator into heat in the environment. This is called damping. Thus, oscillations tend to decay with time unless there is some net source of energy into the system. The simplest description of this decay process can be illustrated by oscillation decay of the harmonic oscillator.
Damped oscillators are created when a resistive force is introduced, which is dependent on the first derivative of the position, or in this case velocity. The differential equation created by Newton's second law adds in this resistive force with an arbitrary constant . This example assumes a linear dependence on velocity.
This equation can be rewritten as before:
where .
This produces the general solution:
where .
The exponential term outside of the parenthesis is the decay function and is the damping coefficient. There are 3 categories of damped oscillators: under-damped, where ; over-damped, where ; and critically damped, where .
Driven oscillations
In addition, an oscillating system may be subject to some external force, as when an AC circuit is connected to an outside power source. In this case the oscillation is said to be '' driven''. The simplest example of this is a spring-mass system with a sinusoidal driving force. where This gives the solution: where and The second term of is the transient solution to the differential equation. The transient solution can be found by using the initial conditions of the system. Some systems can be excited by energy transfer from the environment. This transfer typically occurs where systems are embedded in somefluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...
flow. For example, the phenomenon of flutter in aerodynamics
Aerodynamics () is the study of the motion of atmosphere of Earth, air, particularly when affected by a solid object, such as an airplane wing. It involves topics covered in the field of fluid dynamics and its subfield of gas dynamics, and is an ...
occurs when an arbitrarily small displacement of an aircraft
An aircraft ( aircraft) is a vehicle that is able to flight, fly by gaining support from the Atmosphere of Earth, air. It counters the force of gravity by using either Buoyancy, static lift or the Lift (force), dynamic lift of an airfoil, or, i ...
wing
A wing is a type of fin that produces both Lift (force), lift and drag while moving through air. Wings are defined by two shape characteristics, an airfoil section and a planform (aeronautics), planform. Wing efficiency is expressed as lift-to-d ...
(from its equilibrium) results in an increase in the angle of attack of the wing on the air flow and a consequential increase in lift coefficient, leading to a still greater displacement. At sufficiently large displacements, the stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force.
The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is.
Calculations
The stiffness, k, of a ...
of the wing dominates to provide the restoring force that enables an oscillation.
Resonance
Resonance
Resonance is a phenomenon that occurs when an object or system is subjected to an external force or vibration whose frequency matches a resonant frequency (or resonance frequency) of the system, defined as a frequency that generates a maximu ...
occurs in a damped driven oscillator when ω = ω0, that is, when the driving frequency is equal to the natural frequency of the system. When this occurs, the denominator of the amplitude is minimized, which maximizes the amplitude of the oscillations.
Coupled oscillations
 The harmonic oscillator and the systems it models have a single degree of freedom. More complicated systems have more degrees of freedom, for example, two masses and three springs (each mass being attached to fixed points and to each other). In such cases, the behavior of each variable influences that of the others. This leads to a ''coupling'' of the oscillations of the individual degrees of freedom. For example, two pendulum clocks (of identical frequency) mounted on a common wall will tend to synchronise. This
The harmonic oscillator and the systems it models have a single degree of freedom. More complicated systems have more degrees of freedom, for example, two masses and three springs (each mass being attached to fixed points and to each other). In such cases, the behavior of each variable influences that of the others. This leads to a ''coupling'' of the oscillations of the individual degrees of freedom. For example, two pendulum clocks (of identical frequency) mounted on a common wall will tend to synchronise. This phenomenon
A phenomenon ( phenomena), sometimes spelled phaenomenon, is an observable Event (philosophy), event. The term came into its modern Philosophy, philosophical usage through Immanuel Kant, who contrasted it with the noumenon, which ''cannot'' be ...
was first observed by Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution ...
in 1665. The apparent motions of the compound oscillations typically appears very complicated but a more economic, computationally simpler and conceptually deeper description is given by resolving the motion into normal mode
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies ...
s.
The simplest form of coupled oscillators is a 3 spring, 2 mass system, where masses and spring constants are the same. This problem begins with deriving Newton's second law for both masses.
The equations are then generalized into matrix form.
where , , and
The values of and can be substituted into the matrices.
These matrices can now be plugged into the general solution.
The determinant of this matrix yields a quadratic equation.
Depending on the starting point of the masses, this system has 2 possible frequencies (or a combination of the two). If the masses are started with their displacements in the same direction, the frequency is that of a single mass system, because the middle spring is never extended. If the two masses are started in opposite directions, the second, faster frequency is the frequency of the system.
More special cases are the coupled oscillators where energy alternates between two forms of oscillation. Well-known is the Wilberforce pendulum, where the oscillation alternates between the elongation of a vertical spring and the rotation of an object at the end of that spring.
Coupled oscillators are a common description of two related, but different phenomena. One case is where both oscillations affect each other mutually, which usually leads to the occurrence of a single, entrained oscillation state, where both oscillate with a ''compromise frequency''. Another case is where one external oscillation affects an internal oscillation, but is not affected by this. In this case the regions of synchronization, known as Arnold Tongues, can lead to highly complex phenomena as for instance chaotic dynamics.
Small oscillation approximation
In physics, a system with a set of conservative forces and an equilibrium point can be approximated as a harmonic oscillator near equilibrium. An example of this is the Lennard-Jones potential, where the potential is given by: