|
Classical Limit
The classical limit or correspondence limit is the ability of a physical theory to approximate or "recover" classical mechanics when considered over special values of its parameters. The classical limit is used with physical theories that predict non-classical behavior. Quantum theory A heuristic postulate called the correspondence principle was introduced to quantum theory by Niels Bohr: in effect it states that some kind of continuity argument should apply to the classical limit of quantum systems as the value of the Planck constant normalized by the action of these systems becomes very small. Often, this is approached through "quasi-classical" techniques (cf. WKB approximation). More rigorously, the mathematical operation involved in classical limits is a group contraction, approximating physical systems where the relevant action is much larger than the reduced Planck constant , so the "deformation parameter" / can be effectively taken to be zero (cf. Weyl quantization.) Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain, and predict List of natural phenomena, natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena. The advancement of science generally depends on the interplay between experimental studies and theory. In some cases, theoretical physics adheres to standards of mathematical rigour while giving little weight to experiments and observations.There is some debate as to whether or not theoretical physics uses mathematics to build intuition and illustrativeness to extract physical insight (especially when normal experience fails), rather than as a tool in formalizing theories. This links to the question of it using mathematics in a less formally rigorous, and more intuitive or heuristic way than, say, mathematical physics. For example, while developing special relativity, Albert E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Werner Heisenberg
Werner Karl Heisenberg (; ; 5 December 1901 – 1 February 1976) was a German theoretical physicist, one of the main pioneers of the theory of quantum mechanics and a principal scientist in the German nuclear program during World War II. He published his Umdeutung paper, ''Umdeutung'' paper in 1925, a major reinterpretation of old quantum theory. In the subsequent series of papers with Max Born and Pascual Jordan, during the same year, his matrix mechanics, matrix formulation of quantum mechanics was substantially elaborated. He is known for the uncertainty principle, which he published in 1927. Heisenberg was awarded the 1932 Nobel Prize in Physics "for the creation of quantum mechanics". Heisenberg also made contributions to the theories of the Fluid dynamics, hydrodynamics of turbulent flows, the atomic nucleus, ferromagnetism, cosmic rays, and subatomic particles. He introduced the concept of a wave function collapse. He was also instrumental in planning the first West Germa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Koopman–von Neumann Classical Mechanics
The Koopman–von Neumann (KvN) theory is a description of classical mechanics as an operatorial theory similar to quantum mechanics, based on a Hilbert space of complex, square-integrable wavefunctions. As its name suggests, the KvN theory is related to work by Bernard Koopman and John von Neumann. History Statistical mechanics describes macroscopic systems in terms of statistical ensembles, such as the macroscopic properties of an ideal gas. Ergodic theory is a branch of mathematics arising from the study of statistical mechanics. The origins of the Koopman–von Neumann theory are tightly connected with the rise of ergodic theory as an independent branch of mathematics, in particular with Ludwig Boltzmann's ergodic hypothesis. In 1931, Koopman observed that the phase space of the classical system can be converted into a Hilbert space. According to this formulation, functions representing physical observables become vectors, with an inner product defined in terms of a natu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Review A
''Physical Review A'' (also known as PRA) is a monthly peer-reviewed scientific journal published by the American Physical Society covering atomic, molecular, and optical physics and quantum information. the editor was Jan M. Rost ( Max Planck Institute for the Physics of Complex Systems). History In 1893, the '' Physical Review'' was established at Cornell University. It was taken over by the American Physical Society (formed in 1899) in 1913. In 1970, ''Physical Review'' was subdivided into ''Physical Review A'', ''B'', ''C'', and ''D''. At that time, section ''A'' was subtitled ''Physical Review A: General Physics''. In 1990, a process was started to split this journal into two, resulting in the creation of '' Physical Review E'' in 1993. Hence, in 1993, ''Physical Review A'' changed its statement of scope to ''Atomic, Molecular and Optical Physics.'' In January 2007, the section of ''Physical Review E'' that published papers on classical optics was merged into ''Physical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liouville's Theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical mechanics, statistical and Hamiltonian mechanics. It asserts that ''the phase space, phase-space distribution function is constant along the Trajectory, trajectories of the system''—that is that the density of system points in the vicinity of a given system point traveling through phase-space is constant with time. This time-independent density is in statistical mechanics known as the classical a priori probability. Liouville's theorem applies to conservative systems, that is, systems in which the effects of friction are absent or can be ignored. The general mathematical formulation for such systems is the measure-preserving dynamical system. Liouville's theorem applies when there are degrees of freedom that can be interpreted as positions and momenta; not all measure-preserving dynamical systems have these, but Hamiltonian systems do. The general se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Space Formulation
Phase or phases may refer to: Science *State of matter, or phase, one of the distinct forms in which matter can exist *Phase (matter), a region of space throughout which all physical properties are essentially uniform *Phase space, a mathematical space in which each possible state of a physical system is represented by a point also referred to as a "microscopic state" ** Phase space formulation, a formulation of quantum mechanics in phase space *Phase (waves), the position of a point in time (an instant) on a waveform cycle **Instantaneous phase, generalization for both cyclic and non-cyclic phenomena * AC phase, the phase offset between alternating current electric power in multiple conducting wires **Single-phase electric power, distribution of AC electric power in a system where the voltages of the supply vary in unison **Three-phase electric power, a common method of AC electric power generation, transmission, and distribution *Phase problem, the loss of information (the phase ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
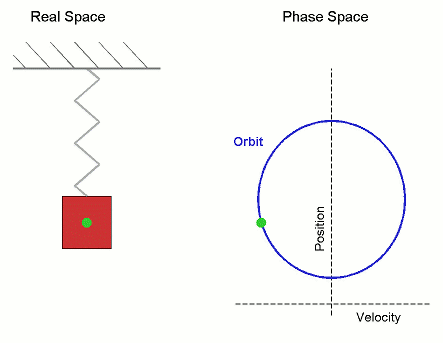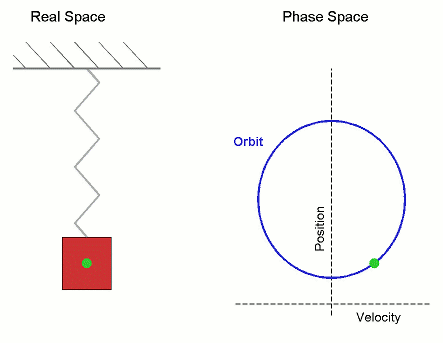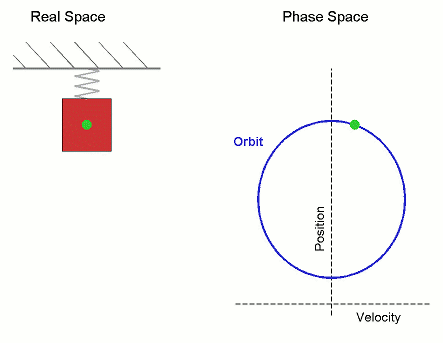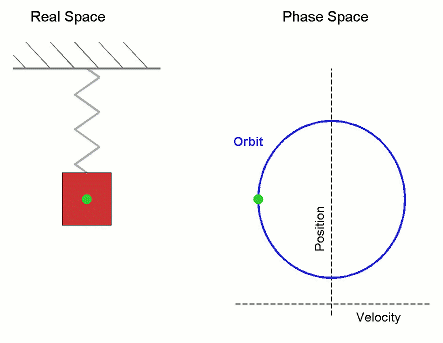
Phase Space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Principles In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, a Hilbert space is a real number, real or complex number, complex inner product space that is also a complete metric space with respect to the metric induced by the inner product. It generalizes the notion of Euclidean space. The inner product allows lengths and angles to be defined. Furthermore, Complete metric space, completeness means that there are enough limit (mathematics), limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space. Hilbert spaces were studied beginning in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, mathematical formulation of quantum mechanics, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chaos
Quantum chaos is a branch of physics focused on how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is: "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle states that classical mechanics is the classical limit of quantum mechanics, specifically in the limit as the ratio of the Planck constant to the action of the system tends to zero. If this is true, then there must be quantum mechanisms underlying classical chaos (although this may not be a fruitful way of examining classical chaos). If quantum mechanics does not demonstrate an exponential sensitivity to initial conditions, how can exponential sensitivity to initial conditions arise in classical chaos, which must be the correspondence principle limit of quantum mechanics? Michael Berry, "Quantum Chaology", pp 104-5 of ''Quantum: a guide for the perplexed'' by Jim Al-Khalili (Weidenfeld ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coherent States
In physics, specifically in quantum mechanics, a coherent state is the specific quantum state of the quantum harmonic oscillator, often described as a state that has dynamics most closely resembling the oscillatory behavior of a classical harmonic oscillator. It was the first example of quantum dynamics when Erwin Schrödinger derived it in 1926, while searching for solutions of the Schrödinger equation that satisfy the correspondence principle. The quantum harmonic oscillator (and hence the coherent states) arise in the quantum theory of a wide range of physical systems.J.R. Klauder and B. Skagerstam, ''Coherent States'', World Scientific, Singapore, 1985. For instance, a coherent state describes the oscillating motion of a particle confined in a quadratic potential well (for an early reference, see e.g. Schiff's textbook). The coherent state describes a state in a system for which the ground-state wavepacket is displaced from the origin of the system. This state can be relat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplitude (see below), which are all functions of the magnitude of the differences between the variable's extreme values. In older texts, the phase of a periodic function is sometimes called the amplitude. Definitions Peak amplitude and semi-amplitude For symmetric periodic waves, like sine waves or triangle waves, ''peak amplitude'' and ''semi amplitude'' are the same. Peak amplitude In audio system measurements, telecommunications and others where the measurand is a signal that swings above and below a reference value but is not sinusoidal, peak amplitude is often used. If the reference is zero, this is the maximum absolute value of the signal; if the reference is a mean value ( DC component), the peak amplitude is the maximum ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Occupation Number
In quantum mechanics, a Fock state or number state is a quantum state that is an element of a Fock space with a well-defined number of particles (or quanta). These states are named after the Soviet physicist Vladimir Fock. Fock states play an important role in the second quantization formulation of quantum mechanics. The particle representation was first treated in detail by Paul Dirac for bosons and by Pascual Jordan and Eugene Wigner for fermions. The Fock states of bosons and fermions obey useful relations with respect to the Fock space creation and annihilation operators. Definition One specifies a multiparticle state of ''N'' non-interacting identical particles by writing the state as a sum of tensor products of ''N'' one-particle states. Additionally, depending on the integrality of the particles' spin, the tensor products must be alternating (anti-symmetric) or symmetric products of the underlying one-particle Hilbert spaces. Specifically: * Fermions, having half-inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |