Morton order on:
[Wikipedia]
[Google]
[Amazon]
 In
In
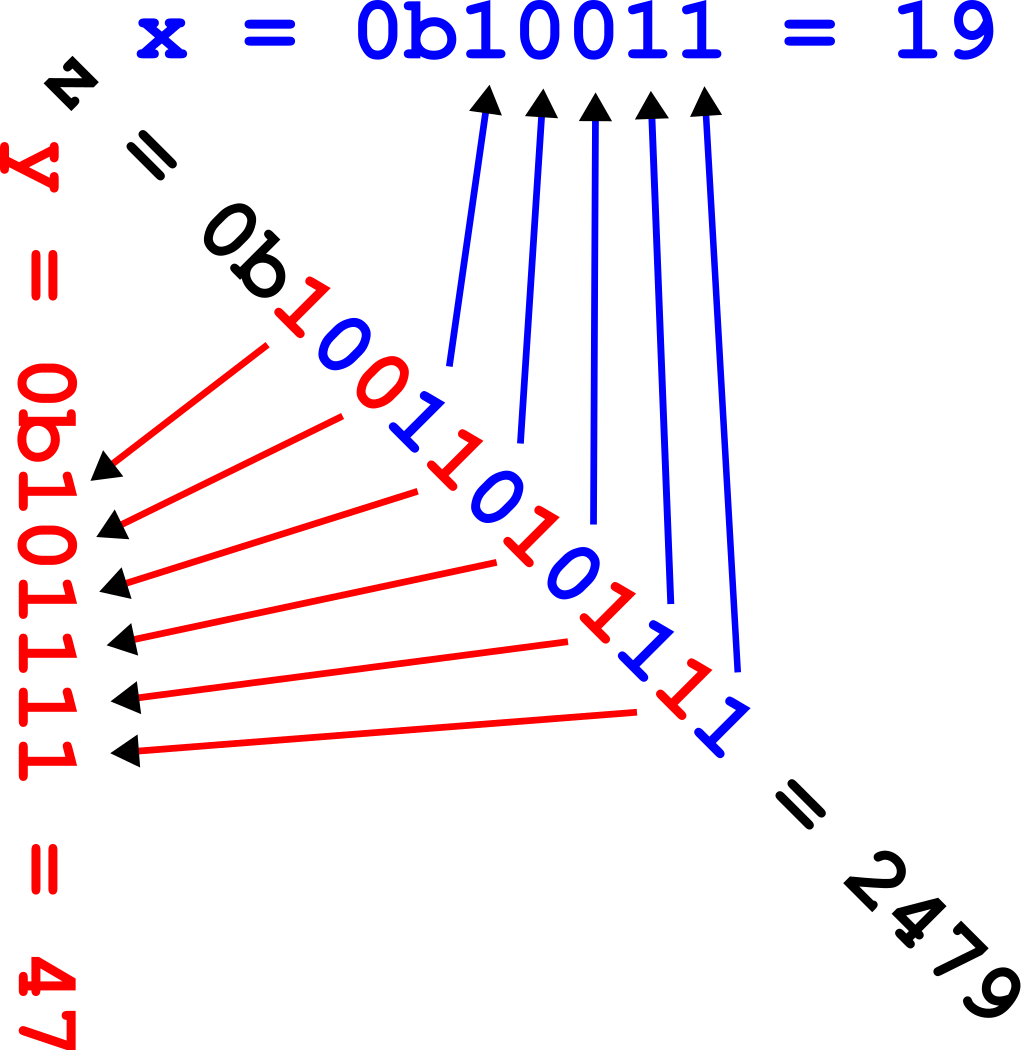 The figure below shows the Z-values for the two dimensional case with integer coordinates 0 ≤ ''x'' ≤ 7, 0 ≤ ''y'' ≤ 7 (shown both in decimal and binary). Interleaving the binary coordinate values (starting to the right with the ''x''-bit (in blue) and alternating to the left with the ''y''-bit (in red)) yields the binary ''z''-values (tilted by 45° as shown). Connecting the ''z''-values in their numerical order produces the recursively Z-shaped curve. Two-dimensional Z-values are also known as quadkey values.
The figure below shows the Z-values for the two dimensional case with integer coordinates 0 ≤ ''x'' ≤ 7, 0 ≤ ''y'' ≤ 7 (shown both in decimal and binary). Interleaving the binary coordinate values (starting to the right with the ''x''-bit (in blue) and alternating to the left with the ''y''-bit (in red)) yields the binary ''z''-values (tilted by 45° as shown). Connecting the ''z''-values in their numerical order produces the recursively Z-shaped curve. Two-dimensional Z-values are also known as quadkey values.
 The Z-values of the ''x'' coordinates are described as binary numbers from the Moser–de Bruijn sequence, having nonzero bits only in their even positions:
x[] =
The sum and difference of two ''x'' values are calculated by using bitwise operations:
x[i+j] = ((x[i] , 0b10101010) + x[j]) & 0b01010101
x[i−j] = ((x[i] & 0b01010101) − x[j]) & 0b01010101 if i ≥ j
This property can be used to offset a Z-value, for example in two dimensions the coordinates to the top (decreasing y), bottom (increasing y), left (decreasing x) and right (increasing x) from the current Z-value ''z'' are:
top = (((z & 0b10101010) − 1) & 0b10101010) , (z & 0b01010101)
bottom = (((z , 0b01010101) + 1) & 0b10101010) , (z & 0b01010101)
left = (((z & 0b01010101) − 1) & 0b01010101) , (z & 0b10101010)
right = (((z , 0b10101010) + 1) & 0b01010101) , (z & 0b10101010)
And in general to add two two-dimensional Z-values ''w'' and ''z'':
sum = ((z , 0b10101010) + (w & 0b01010101) & 0b01010101) , ((z , 0b01010101) + (w & 0b10101010) & 0b10101010)
The Z-values of the ''x'' coordinates are described as binary numbers from the Moser–de Bruijn sequence, having nonzero bits only in their even positions:
x[] =
The sum and difference of two ''x'' values are calculated by using bitwise operations:
x[i+j] = ((x[i] , 0b10101010) + x[j]) & 0b01010101
x[i−j] = ((x[i] & 0b01010101) − x[j]) & 0b01010101 if i ≥ j
This property can be used to offset a Z-value, for example in two dimensions the coordinates to the top (decreasing y), bottom (increasing y), left (decreasing x) and right (increasing x) from the current Z-value ''z'' are:
top = (((z & 0b10101010) − 1) & 0b10101010) , (z & 0b01010101)
bottom = (((z , 0b01010101) + 1) & 0b10101010) , (z & 0b01010101)
left = (((z & 0b01010101) − 1) & 0b01010101) , (z & 0b10101010)
right = (((z , 0b10101010) + 1) & 0b01010101) , (z & 0b10101010)
And in general to add two two-dimensional Z-values ''w'' and ''z'':
sum = ((z , 0b10101010) + (w & 0b01010101) & 0b01010101) , ((z , 0b01010101) + (w & 0b10101010) & 0b10101010)
def cmp_zorder(lhs, rhs) -> bool:
"""Compare z-ordering."""
# Assume lhs and rhs array-like objects of indices.
assert len(lhs) len(rhs)
# Will contain the most significant dimension.
msd = 0
# Loop over the other dimensions.
for dim in range(1, len(lhs)):
# Check if the current dimension is more significant
# by comparing the most significant bits.
if less_msb(lhs sd^ rhs sd lhs im^ rhs im:
msd = dim
return lhs sd< rhs sd
One way to determine whether the most significant bit is smaller is to compare the floor of the base-2 logarithm of each point. It turns out the following operation is equivalent, and only requires exclusive or operations:
def less_msb(x: int, y: int) -> bool:
return x < y and x < (x ^ y)
It is also possible to compare floating point numbers using the same technique. The
 In this example, the range being queried (''x'' = 2, ..., 3, ''y'' = 2, ..., 6) is indicated by the dotted rectangle. Its highest Z-value (MAX) is 45. In this example, the value ''F'' = 19 is encountered when searching a data structure in increasing Z-value direction, so we would have to search in the interval between ''F'' and MAX (hatched area). To speed up the search, one would calculate the next Z-value which is in the search range, called BIGMIN (36 in the example) and only search in the interval between BIGMIN and MAX (bold values), thus skipping most of the hatched area. Searching in decreasing direction is analogous with LITMAX which is the highest Z-value in the query range lower than ''F''. The BIGMIN problem has first been stated and its solution shown in Tropf and Herzog. For the history after the puplication see.
An extensive explanation of the LITMAX/BIGMIN calculation algorithm, together with Pascal Source Code (3D, easy to adapt to nD) and hints on how to handle floating point data and possibly negative data, is provide
In this example, the range being queried (''x'' = 2, ..., 3, ''y'' = 2, ..., 6) is indicated by the dotted rectangle. Its highest Z-value (MAX) is 45. In this example, the value ''F'' = 19 is encountered when searching a data structure in increasing Z-value direction, so we would have to search in the interval between ''F'' and MAX (hatched area). To speed up the search, one would calculate the next Z-value which is in the search range, called BIGMIN (36 in the example) and only search in the interval between BIGMIN and MAX (bold values), thus skipping most of the hatched area. Searching in decreasing direction is analogous with LITMAX which is the highest Z-value in the query range lower than ''F''. The BIGMIN problem has first been stated and its solution shown in Tropf and Herzog. For the history after the puplication see.
An extensive explanation of the LITMAX/BIGMIN calculation algorithm, together with Pascal Source Code (3D, easy to adapt to nD) and hints on how to handle floating point data and possibly negative data, is provide
2021 by Tropf
Here, bit interleaving is not done explicitly; the data structure has just pointers to the original (unsorted) database records. With a general record comparison function (greater-less-equal, in the sense of z-value), complications with bit sequences length exceeding the computer word length are avoided, and the code can easily be adapted to any number of dimensions and any record key word length. As the approach does not depend on the one dimensional data structure chosen, there is still free choice of structuring the data, so well known methods such as balanced trees can be used to cope with dynamic data, and keeping the tree balance when inserting or deleting takes O(log n) time. The method is also used in UB-trees (balanced). The Free choice makes it easier to incorporate the method into existing databases. This is in contrast for example to
STANN: A library for approximate nearest neighbor search, using Z-order curve
Sean Eron Anderson, Stanford University Fractal curves Database algorithms Geometric data structures Database index techniques Linear algebra
mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series ( ...
and computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, functions which are Z-order, Lebesgue curve, Morton space-filling curve
In mathematical analysis, a space-filling curve is a curve whose Range of a function, range reaches every point in a higher dimensional region, typically the unit square (or more generally an ''n''-dimensional unit hypercube). Because Giuseppe Pea ...
, Morton order or Morton code map multidimensional data to one dimension while preserving locality of the data points (two points close together in multidimensions with high probability lie also close together in Morton order). It is named in France after Henri Lebesgue
Henri Léon Lebesgue (; ; June 28, 1875 – July 26, 1941) was a French mathematician known for his Lebesgue integration, theory of integration, which was a generalization of the 17th-century concept of integration—summing the area between an ...
, who studied it in 1904, and named in the United States after Guy Macdonald Morton, who first applied the order to file sequencing in 1966. The z-value of a point in multidimensions is simply calculated by bit interleaving the binary representations of its coordinate values. However, when querying a multidimensional search range in these data, using binary search is not really efficient: It is necessary for calculating, from a point encountered in the data structure, the next possible Z-value which is in the multidimensional search range, called BIGMIN. The BIGMIN problem has first been stated and its solution shown by Tropf and Herzog in 1981. Once the data are sorted by bit interleaving, any one-dimensional data structure can be used, such as simple one dimensional arrays
An array is a systematic arrangement of similar objects, usually in rows and columns.
Things called an array include:
{{TOC right
Music
* In twelve-tone and serial composition, the presentation of simultaneous twelve-tone sets such that the ...
, binary search tree
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a Rooted tree, rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left ...
s, B-tree
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing fo ...
s, skip lists or (with low significant bits truncated) hash table
In computer science, a hash table is a data structure that implements an associative array, also called a dictionary or simply map; an associative array is an abstract data type that maps Unique key, keys to Value (computer science), values. ...
s. The resulting ordering can equivalently be described as the order one would get from a depth-first traversal of a quadtree or octree
An octree is a tree data structure in which each internal node has exactly eight child node, children. Octrees are most often used to partition a three-dimensional space by recursive subdivision, recursively subdividing it into eight Octant (geo ...
.
Coordinate values
 The figure below shows the Z-values for the two dimensional case with integer coordinates 0 ≤ ''x'' ≤ 7, 0 ≤ ''y'' ≤ 7 (shown both in decimal and binary). Interleaving the binary coordinate values (starting to the right with the ''x''-bit (in blue) and alternating to the left with the ''y''-bit (in red)) yields the binary ''z''-values (tilted by 45° as shown). Connecting the ''z''-values in their numerical order produces the recursively Z-shaped curve. Two-dimensional Z-values are also known as quadkey values.
The figure below shows the Z-values for the two dimensional case with integer coordinates 0 ≤ ''x'' ≤ 7, 0 ≤ ''y'' ≤ 7 (shown both in decimal and binary). Interleaving the binary coordinate values (starting to the right with the ''x''-bit (in blue) and alternating to the left with the ''y''-bit (in red)) yields the binary ''z''-values (tilted by 45° as shown). Connecting the ''z''-values in their numerical order produces the recursively Z-shaped curve. Two-dimensional Z-values are also known as quadkey values.
Efficiently building quadtrees and octrees
The Z-ordering can be used to efficiently build a quadtree (2D) oroctree
An octree is a tree data structure in which each internal node has exactly eight child node, children. Octrees are most often used to partition a three-dimensional space by recursive subdivision, recursively subdividing it into eight Octant (geo ...
(3D) for a set of points.. The basic idea is to sort the input set according to Z-order. Once sorted, the points can either be stored in a binary search tree and used directly, which is called a linear quadtree, or they can be used to build a pointer based quadtree.
The input points are usually scaled in each dimension to be positive integers, either as a fixed point representation over the unit range or corresponding to the machine word size. Both representations are equivalent and allow for the highest order non-zero bit to be found in constant time. Each square in the quadtree has a side length which is a power of two, and corner coordinates which are multiples of the side length. Given any two points, the ''derived square'' for the two points is the smallest square covering both points. The interleaving of bits from the ''x'' and ''y'' components of each point is called the ''shuffle'' of ''x'' and ''y'', and can be extended to higher dimensions.
Points can be sorted according to their shuffle without explicitly interleaving the bits. To do this, for each dimension, the most significant bit of the exclusive or
Exclusive or, exclusive disjunction, exclusive alternation, logical non-equivalence, or logical inequality is a logical operator whose negation is the logical biconditional. With two inputs, XOR is true if and only if the inputs differ (on ...
of the coordinates of the two points for that dimension is examined. The dimension for which the most significant bit is largest is then used to compare the two points to determine their shuffle order.
The exclusive or operation masks off the higher order bits for which the two coordinates are identical. Since the shuffle interleaves bits from higher order to lower order, identifying the coordinate with the largest most significant bit, identifies the first bit in the shuffle order which differs, and that coordinate can be used to compare the two points.. This is shown in the following Python code:
less_msb function is modified to first compare the exponents. Only when they are equal is the standard less_msb function used on the mantissas.
Once the points are in sorted order, two properties make it easy to build a quadtree: The first is that the points contained in a square of the quadtree form a contiguous interval in the sorted order. The second is that if more than one child of a square contains an input point, the square is the ''derived square'' for two adjacent points in the sorted order.
For each adjacent pair of points, the derived square is computed and its side length determined. For each derived square, the interval containing it is bounded by the first larger square to the right and to the left in sorted order. Each such interval corresponds to a square in the quadtree. The result of this is a compressed quadtree, where only nodes containing input points or two or more children are present. A non-compressed quadtree can be built by restoring the missing nodes, if desired.
Rather than building a pointer based quadtree, the points can be maintained in sorted order in a data structure such as a binary search tree. This allows points to be added and deleted in time. Two quadtrees can be merged by merging the two sorted sets of points, and removing duplicates. Point location can be done by searching for the points preceding and following the query point in the sorted order. If the quadtree is compressed, the predecessor node found may be an arbitrary leaf inside the compressed node of interest. In this case, it is necessary to find the predecessor of the least common ancestor of the query point and the leaf found.
Use with one-dimensional data structures for range searching
By bit interleaving, the database records are converted to a (possibly very long) sequence of bits. The bit sequences are interpreted as binary numbers and the data are sorted or indexed by the binary values, using any one dimensional data structure, as mentioned in the introduction. However, when querying a multidimensional search range in these data, using binary search is not really efficient. Although Z-order is preserving locality well, for efficient range searches an algorithm is necessary for calculating, from a point encountered in the data structure, the next possible Z-value which is in the multidimensional search range:2021 by Tropf
Here, bit interleaving is not done explicitly; the data structure has just pointers to the original (unsorted) database records. With a general record comparison function (greater-less-equal, in the sense of z-value), complications with bit sequences length exceeding the computer word length are avoided, and the code can easily be adapted to any number of dimensions and any record key word length. As the approach does not depend on the one dimensional data structure chosen, there is still free choice of structuring the data, so well known methods such as balanced trees can be used to cope with dynamic data, and keeping the tree balance when inserting or deleting takes O(log n) time. The method is also used in UB-trees (balanced). The Free choice makes it easier to incorporate the method into existing databases. This is in contrast for example to
R-tree
R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons. The R-tree was proposed by Antonin Guttman in 1984 and has found s ...
s where special considerations are necessary.
Applying the method hierarchically (according to the data structure at hand), optionally in both increasing and decreasing direction, yields highly efficient multidimensional range search which is important in both commercial and technical applications, e.g. as a procedure underlying nearest neighbour searches. Z-order is one of the few multidimensional access methods that has found its way into commercial database systems. The method is used in various technical applications of different fields. and in commercial database systems.
As long ago as 1966, G.M.Morton proposed Z-order for file sequencing of a static two dimensional geographical database. Areal data units are contained in one or a few quadratic frames represented by their sizes and lower right corner Z-values, the sizes complying with the Z-order hierarchy at the corner position. With high probability, changing to an adjacent frame is done with one or a few relatively small scanning steps.
Related structures
As an alternative, the Hilbert curve has been suggested as it has a better order-preserving behaviour, and, in fact, was used in an optimized index, the S2-geometry.Applications
Linear algebra
The Strassen algorithm for matrix multiplication is based on splitting the matrices in four blocks, and then recursively splitting each of these blocks in four smaller blocks, until the blocks are single elements (or more practically: until reaching matrices so small that the Moser–de Bruijn sequence trivial algorithm is faster). Arranging the matrix elements in Z-order then improves locality, and has the additional advantage (compared to row- or column-major ordering) that the subroutine for multiplying two blocks does not need to know the total size of the matrix, but only the size of the blocks and their location in memory. Effective use of Strassen multiplication with Z-order has been demonstrated, see Valsalam and Skjellum's 2002 paper. Buluç ''et al.'' present asparse matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse ...
data structure that Z-orders its non-zero elements to enable parallel matrix-vector multiplication.
Matrices in linear algebra can also be traversed using a space-filling curve. Conventional loops traverse a matrix row by row. Traversing with the Z-curve allows efficient access to the memory hierarchy
In computer architecture, the memory hierarchy separates computer storage into a hierarchy based on response time. Since response time, complexity, and capacity are related, the levels may also be distinguished by their performance and contr ...
.Martin Perdacher, Claudia Plant, Christian Böhm: Improved Data Locality Using Morton-order Curve on the Example of LU Decomposition. IEEE BigData 2020: pp. 351–360
Texture mapping
Some GPUs store texture maps in Z-order to increase spatiallocality of reference
In computer science, locality of reference, also known as the principle of locality, is the tendency of a processor to access the same set of memory locations repetitively over a short period of time. There are two basic types of reference localit ...
during texture mapped rasterization. This allows cache lines to represent rectangular tiles, increasing the probability that nearby accesses are in the cache. At a larger scale, it also decreases the probability of costly, so called, "page breaks" (i.e., the cost of changing rows) in SDRAM/DDRAM. This is important because 3D rendering involves arbitrary transformations (rotations, scaling, perspective, and distortion by animated surfaces).
These formats are often referred to as ''swizzled textures'' or ''twiddled textures''. Other tiled formats may also be used.
''n''-body problem
The Barnes–Hut algorithm requires construction of an octree. Storing the data as a pointer-based tree requires many sequential pointer dereferences to iterate over the octree in depth-first order (expensive on a distributed-memory machine). Instead, if one stores the data in a hashtable, using octree hashing, the Z-order curve naturally iterates the octree in depth-first order.See also
* Geohash *Hilbert R-tree
Hilbert R-tree, an R-tree variant, is an index for multidimensional objects such as lines, regions, 3-D objects, or high-dimensional feature-based parametric objects. It can be thought of as an extension to B+-tree for multidimensional objects.
T ...
* Linear algebra
Linear algebra is the branch of mathematics concerning linear equations such as
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrix (mathemat ...
* Locality preserving hashing
* Matrix representation
* Netto's theorem
* PH-tree
* Spatial index
A spatial database is a general-purpose database (usually a relational database) that has been enhanced to include spatial data that represents objects defined in a geometric space, along with tools for querying and analyzing such data.
Most ...
References
{{reflistExternal links
STANN: A library for approximate nearest neighbor search, using Z-order curve
Sean Eron Anderson, Stanford University Fractal curves Database algorithms Geometric data structures Database index techniques Linear algebra