Mixed Models

A mixed model, mixed-effects model or mixed error-component model is a statistical model containing both fixed effects and random effects. These models are useful in a wide variety of disciplines in the physical, biological and social sciences.
They are particularly useful in settings where repeated measurements are made on the same statistical units (see also longitudinal study), or where measurements are made on clusters of related statistical units. Mixed models are often preferred over traditional analysis of variance regression models because they don't rely on the independent observations assumption. Further, they have their flexibility in dealing with missing values and uneven spacing of repeated measurements. The Mixed model analysis allows measurements to be explicitly modeled in a wider variety of correlation and variance-covariance avoiding biased estimations structures.

This page will discuss mainly linear mixed-effects models rather than generalized linear mixed models or nonlinear mixed-effects models.

Qualitative Description

Linear mixed models (LMMs) are statistical models that incorporate fixed and random effects to accurately represent non-independent data structures. LMM is an alternative to analysis of variance. Often, ANOVA assumes the independence of observations within each group, however, this assumption may not hold in non-independent data, such as multilevel/hierarchical, longitudinal, or correlated datasets.

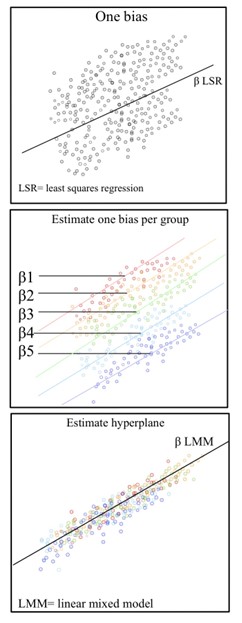
Non-independent sets are ones in which the variability between outcomes is due to correlations within groups or between groups. Mixed models properly account for nest structures/hierarchical data structures where observations are influenced by their nested associations. For example, when studying education methods involving multiple schools, there are multiple levels of variables to consider. The individual level/lower level comprises individual students or teachers within the school. The observations obtained from this student/teacher is nested within their school. For example, Student A is a unit within the School A. The next higher level is the school. At the higher level, the school contains multiple individual students and teachers. The school level influences the observations obtained from the students and teachers. For Example, School A and School B are the higher levels each with its set of Student A and Student B respectively. This represents a hierarchical data scheme. A solution to modeling hierarchical data is using linear mixed models.

LMMs allow us to understand the important effects between and within levels while incorporating the corrections for standard errors for non-independence embedded in the data structure. In experimental fields such as social psychology, psycholinguistics, cognitive psychology (and neuroscience), where studies often involve multiple grouping variables, failing to account for random effects can lead to inflated Type I error rates and unreliable conclusions. For instance, when analyzing data from experiments that involve both samples of participants and samples of stimuli (e.g., images, scenarios, etc.), ignoring variation in either of these grouping variables (e.g., by averaging over stimuli) can result in misleading conclusions. In such cases, researchers can instead treat both participant and stimulus as random effects with LMMs, and in doing so, can correctly account for the variation in their data across multiple grouping variables. Similarly, when analyzing data from comparative longitudinal surveys, failing to include random effects at all relevant levels—such as country and country-year—can significantly distort the results.

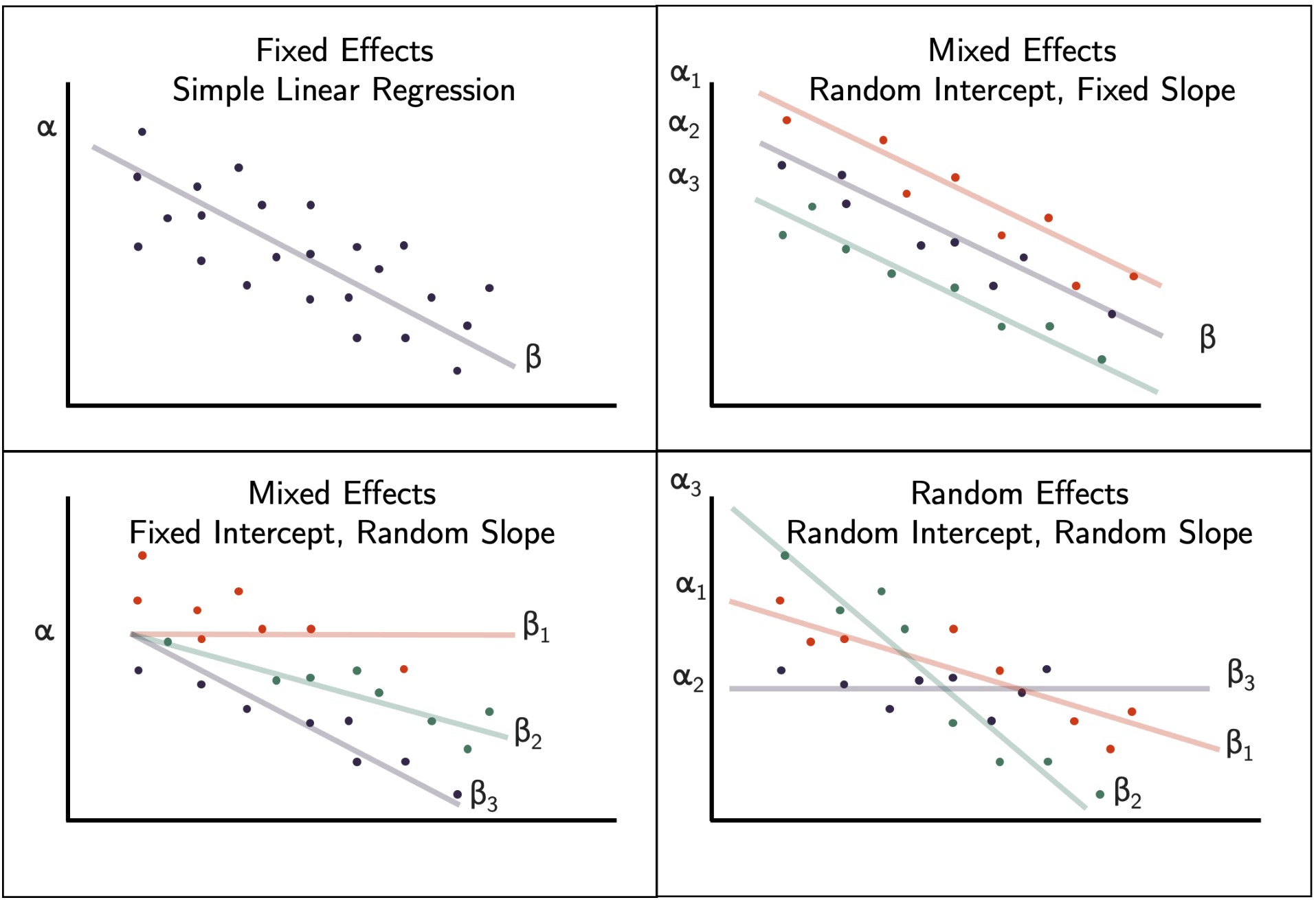
The Fixed Effect

Fixed effects encapsulate the tendencies/trends that are consistent at the levels of primary interest. These effects are considered fixed because they are non-random and assumed to be constant for the population being studied. For example, when studying education a fixed effect could represent overall school level effects that are consistent across all schools.

While the hierarchy of the data set is typically obvious, the specific fixed effects that affect the average responses for all subjects must be specified. Some fixed effect coefficients are sufficient without corresponding random effects where as other fixed coefficients only represent an average where the individual units are random. These may be determined by incorporating random intercepts and slopes.

In most situations, several related models are considered and the model that best represents a universal model is adopted.

The Random Effect, ε

A key component of the mixed model is the incorporation of random effects with the fixed effect. Fixed effects are often fitted to represent the underlying model. In Linear mixed models, the true regression of the population is linear, β. The fixed data is fitted at the highest level. Random effects introduce statistical variability at different levels of the data hierarchy. These account for the unmeasured sources of variance that affect certain groups in the data. For example, the differences between student 1 and student 2 in the same class, or the differences between class 1 and class 2 in the same school.

History and current status

Ronald Fisher introduced random effects models to study the correlations of trait values between relatives. In the 1950s, Charles Roy Henderson
provided best linear unbiased estimates of fixed effects and best linear unbiased predictions of random effects. Subsequently, mixed modeling has become a major area of statistical research, including work on computation of maximum likelihood estimates, non-linear mixed effects models, missing data in mixed effects models, and Bayesian estimation of mixed effects models. Mixed models are applied in many disciplines where multiple correlated measurements are made on each unit of interest. They are prominently used in research involving human and animal subjects in fields ranging from genetics to marketing, and have also been used in baseball and industrial statistics.
The mixed linear model association has improved the prevention of false positive associations. Populations are deeply interconnected and the relatedness structure of population dynamics is extremely difficult to model without the use of mixed models. Linear mixed models may not, however, be the only solution. LMM's have a constant- residual variance assumption that is sometimes violated when accounting for deeply associated continuous and binary traits.

Definition

In matrix notation a linear mixed model can be represented as

:$\boldsymbol = X \boldsymbol + Z \boldsymbol + \boldsymbol$

where

*$\boldsymbol$ is a known vector of observations, with mean $E(\boldsymbol) = X \boldsymbol$;
*$\boldsymbol$ is an unknown vector of fixed effects;
*$\boldsymbol$ is an unknown vector of random effects, with mean $E(\boldsymbol)=\boldsymbol$ and variance–covariance matrix $\operatorname(\boldsymbol)=G$;
*$\boldsymbol$ is an unknown vector of random errors, with mean $E(\boldsymbol)=\boldsymbol$ and variance $\operatorname(\boldsymbol)=R$;
*$X$ is the known design matrix for the fixed effects relating the observations $\boldsymbol$ to $\boldsymbol$, respectively
* $Z$ is the known design matrix for the random effects relating the observations $\boldsymbol$ to $\boldsymbol$, respectively.

For example, if each observation can belong to any zero or more of categories then , which has one row per observation, can be chosen to have columns, where a value of for a matrix element of indicates that an observation is known to belong to a category and a value of indicates that an observation is known to not belong to a category. The inferred value of for a category is then a category-specific intercept. If has additional columns, where the non-zero values are instead the value of an independent variable for an observation, then the corresponding inferred value of is a category-specific slope for that independent variable. The prior distribution for the category intercepts and slopes is described by the covariance matrix .

Estimation

The joint density of $\boldsymbol$ and $\boldsymbol$ can be written as: $f(\boldsymbol,\boldsymbol) = f(\boldsymbol , \boldsymbol) \, f(\boldsymbol)$.
Assuming normality, $\boldsymbol \sim \mathcal(\boldsymbol,G)$, $\boldsymbol \sim \mathcal(\boldsymbol,R)$ and $\mathrm(\boldsymbol,\boldsymbol)=\boldsymbol$, and maximizing the joint density over $\boldsymbol$ and $\boldsymbol$, gives Henderson's "mixed model equations" (MME) for linear mixed models:

:$\begin X'R^X & X'R^Z \\ Z'R^X & Z'R^Z + G^ \end \begin \hat \\ \hat \end = \begin X'R^\boldsymbol \\ Z'R^\boldsymbol \end$
where for example is the matrix transpose of and is the matrix inverse of .

The solutions to the MME, $\textstyle\hat$ and $\textstyle\hat$ are best linear unbiased estimates and predictors for $\boldsymbol$ and $\boldsymbol$, respectively. This is a consequence of the Gauss–Markov theorem when the conditional variance of the outcome is not scalable to the identity matrix. When the conditional variance is known, then the inverse variance weighted least squares estimate is best linear unbiased estimates. However, the conditional variance is rarely, if ever, known. So it is desirable to jointly estimate the variance and weighted parameter estimates when solving MMEs.

Choice of random effects structure

One choice that analysts face with mixed models is which random effects (i.e., grouping variables, random intercepts, and random slopes) to include. One prominent recommendation in the context of confirmatory hypothesis testing is to adopt a "maximal" random effects structure, including all possible random effects justified by the experimental design, as a means to control Type I error rates.

Software

One method used to fit such mixed models is that of the expectation–maximization algorithm (EM) where the variance components are treated as unobserved nuisance parameters in the joint likelihood. Currently, this is the method implemented in statistical software such as Python (statsmodels package) and SAS (proc mixed), and as initial step only in R's nlme package lme(). The solution to the mixed model equations is a maximum likelihood estimate when the distribution of the errors is normal.

There are several other methods to fit mixed models, including using a mixed effect model (MEM) initially, and then Newton-Raphson (used by R package nlme's lme()), penalized least squares to get a profiled log likelihood only depending on the (low-dimensional) variance-covariance parameters of $\boldsymbol$, i.e., its cov matrix $\boldsymbol$, and then modern direct optimization for that reduced objective function (used by R's lme4 package lmer() and the Julia package MixedModels.jl) and direct optimization of the likelihood (used by e.g. R's glmmTMB). Notably, while the canonical form proposed by Henderson is useful for theory, many popular software packages use a different formulation for numerical computation in order to take advantage of sparse matrix methods (e.g. lme4 and MixedModels.jl).

In the context of Bayesian methods, the brms package provides a user-friendly interface for fitting mixed models in R using Stan, allowing for the incorporation of prior distributions and the estimation of posterior distributions. In python, Bambi provides a similarly streamlined approach for fitting mixed effects models using PyMC.

See also

* Nonlinear mixed-effects model
* Fixed effects model
* Generalized linear mixed model
* Linear regression
* Mixed-design analysis of variance
* Multilevel model
* Random effects model
* Repeated measures design
* Empirical Bayes method

References

Further reading

*
*
*

{{DEFAULTSORT:Mixed Model
Regression models
Analysis of variance