|
Random Effect
In econometrics, a random effects model, also called a variance components model, is a statistical model where the model parameters are random variables. It is a kind of hierarchical linear model, which assumes that the data being analysed are drawn from a hierarchy of different populations whose differences relate to that hierarchy. A random effects model is a special case of a mixed model. Contrast this to the biostatistics definitions, as biostatisticians use "fixed" and "random" effects to respectively refer to the population-average and subject-specific effects (and where the latter are generally assumed to be unknown, latent variables). Qualitative description Random effect models assist in controlling for unobserved heterogeneity when the heterogeneity is constant over time and not correlated with independent variables. This constant can be removed from longitudinal data through differencing, since taking a first difference will remove any time invariant components of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Econometrics
Econometrics is an application of statistical methods to economic data in order to give empirical content to economic relationships. M. Hashem Pesaran (1987). "Econometrics", '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8–22 Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1 p. 1–34Abstract ( 2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference." An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships." Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today. A basic tool for econometrics is the multiple linear regression model. ''Econome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Mean Square
In statistics, expected mean squares (EMS) are the expected values of certain statistics arising in partitions of sums of squares in the analysis of variance (ANOVA). They can be used for ascertaining which statistic should appear in the denominator in an F-test for testing a null hypothesis that a particular effect is absent. Definition When the total corrected sum of squares in an ANOVA is partitioned into several components, each attributed to the effect of a particular predictor variable, each of the sums of squares in that partition is a random variable that has an expected value. That expected value divided by the corresponding number of degrees of freedom is the expected mean square for that predictor variable. Example The following example is from ''Longitudinal Data Analysis'' by Donald Hedeker and Robert D. Gibbons. Donald Hedeker, Robert D. Gibbons. ''Longitudinal Data Analysis.'' Wiley Interscience. 2006. pp. 21–24 Each of ''s'' treatments (one of which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
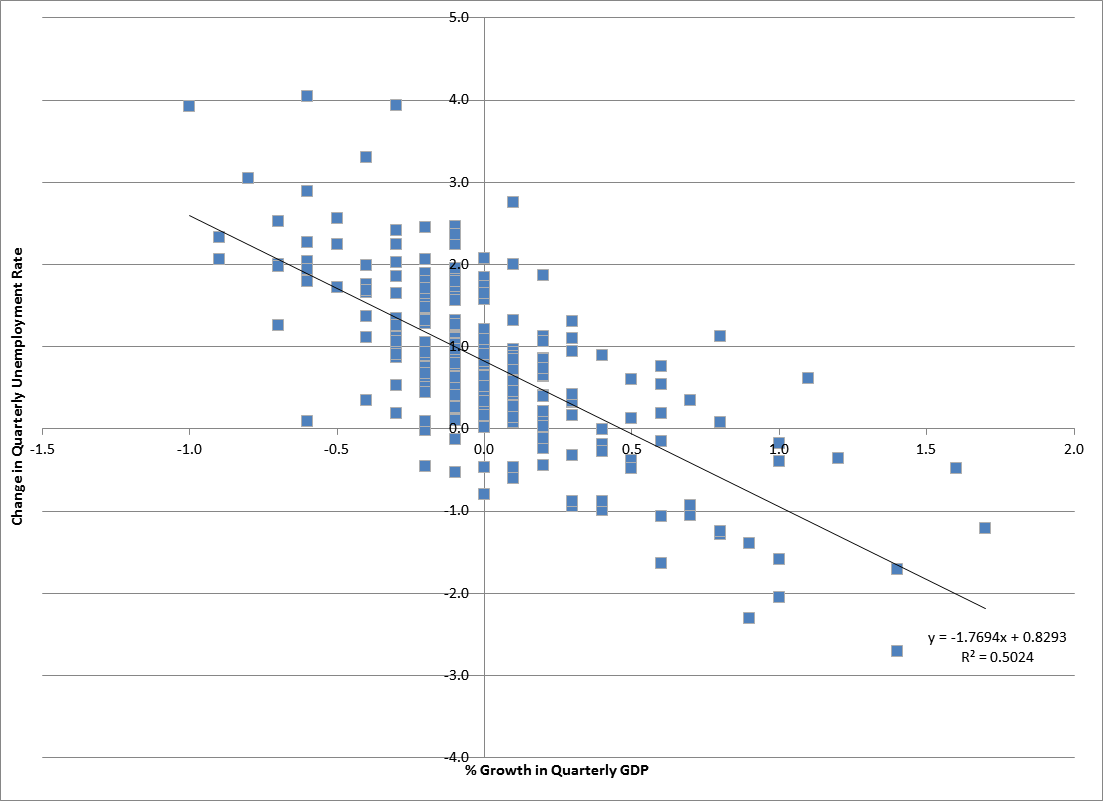
Panel Analysis
Panel (data) analysis is a statistical method, widely used in social science, epidemiology, and econometrics to analyze two-dimensional (typically cross sectional and longitudinal) panel data. The data are usually collected over time and over the same individuals and then a regression is run over these two dimensions. Multidimensional analysis is an econometric method in which data are collected over more than two dimensions (typically, time, individuals, and some third dimension). A common panel data regression model looks like y_=a+bx_+\varepsilon_, where y is the dependent variable, x is the independent variable, a and b are coefficients, i and t are indices for individuals and time. The error \varepsilon_ is very important in this analysis. Assumptions about the error term determine whether we speak of fixed effects or random effects. In a fixed effects model, \varepsilon_ is assumed to vary non-stochastically over i or t making the fixed effects model analogous to a dummy va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Variance
In probability theory and statistics, a conditional variance is the variance of a random variable given the value(s) of one or more other variables. Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function. Conditional variances are important parts of autoregressive conditional heteroskedasticity (ARCH) models. Definition The conditional variance of a random variable ''Y'' given another random variable ''X'' is :\operatorname(Y\mid X) = \operatorname\Big(\big(Y - \operatorname(Y\mid X)\big)^\;\Big, \; X\Big). The conditional variance tells us how much variance is left if we use \operatorname(Y\mid X) to "predict" ''Y''. Here, as usual, \operatorname(Y\mid X) stands for the conditional expectation of ''Y'' given ''X'', which we may recall, is a random variable itself (a function of ''X'', determined up to probability one). As a result, \operatorname(Y\mid X) itself is a random variable (and is a function of ''X''). Expl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance Estimation
In statistics, sometimes the covariance matrix of a multivariate random variable is not known but has to be estimated. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution. Simple cases, where observations are complete, can be dealt with by using the sample covariance matrix. The sample covariance matrix (SCM) is an unbiased and efficient estimator of the covariance matrix if the space of covariance matrices is viewed as an extrinsic convex cone in R''p''×''p''; however, measured using the intrinsic geometry of positive-definite matrices, the SCM is a biased and inefficient estimator. In addition, if the random variable has a normal distribution, the sample covariance matrix has a Wishart distribution and a slightly differently scaled version of it is the maximum likelihood estimate. Cases involving missing data, heteroscedasticity, or autocorrelated res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MINQUE
In statistics, the theory of minimum norm quadratic unbiased estimation (MINQUE) was developed by C. R. Rao. MINQUE is a theory alongside other estimation methods in estimation theory, such as the method of moments or maximum likelihood estimation. Similar to the theory of best linear unbiased estimation, MINQUE is specifically concerned with linear regression models. The method was originally conceived to estimate heteroscedastic error variance in multiple linear regression. MINQUE estimators also provide an alternative to maximum likelihood estimators or restricted maximum likelihood estimators for variance components in mixed effects models. MINQUE estimators are quadratic forms of the response variable and are used to estimate a linear function of the variances. Principles We are concerned with a mixed effects model for the random vector \mathbf \in \mathbb^n with the following linear structure. \mathbf = \mathbf\boldsymbol\beta + \mathbf_1 \boldsymbol\xi_1 + \cdots ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Effects
In statistics, a fixed effects model is a statistical model in which the model parameters are fixed or non-random quantities. This is in contrast to random effects models and mixed models in which all or some of the model parameters are random variables. In many applications including econometrics and biostatistics a fixed effects model refers to a regression model in which the group means are fixed (non-random) as opposed to a random effects model in which the group means are a random sample from a population. Generally, data can be grouped according to several observed factors. The group means could be modeled as fixed or random effects for each grouping. In a fixed effects model each group mean is a group-specific fixed quantity. In panel data where longitudinal observations exist for the same subject, fixed effects represent the subject-specific means. In panel data analysis the term fixed effects estimator (also known as the within estimator) is used to refer to an estimat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hierarchical Linear Modeling
Multilevel models are statistical models of parameters that vary at more than one level. An example could be a model of student performance that contains measures for individual students as well as measures for classrooms within which the students are grouped. These models can be seen as generalizations of linear models (in particular, linear regression), although they can also extend to non-linear models. These models became much more popular after sufficient computing power and software became available. Multilevel models are particularly appropriate for research designs where data for participants are organized at more than one level (i.e., nested data). The units of analysis are usually individuals (at a lower level) who are nested within contextual/aggregate units (at a higher level). While the lowest level of data in multilevel models is usually an individual, repeated measurements of individuals may also be examined. As such, multilevel models provide an alternative type ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Area Estimation
Small area estimation is any of several statistical techniques involving the estimation of parameters for small sub-populations, generally used when the sub-population of interest is included in a larger survey. The term "small area" in this context generally refers to a small geographical area such as a county. It may also refer to a "small domain", i.e. a particular demographic within an area. If a survey has been carried out for the population as a whole (for example, a nation or statewide survey), the sample size within any particular small area may be too small to generate accurate estimates from the data. To deal with this problem, it may be possible to use additional data (such as census records) that exists for these small areas in order to obtain estimates. One of the more common small area models A model is an informative representation of an object, person, or system. The term originally denoted the plans of a building in late 16th-century English, and derived via ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bühlmann Model
In credibility theory, a branch of study in actuarial science, the Bühlmann model is a random effects model (or "variance components model" or hierarchical linear model) used to determine the appropriate premium for a group of insurance contracts. The model is named after Hans Bühlmann who first published a description in 1967. Model description Consider ''i'' risks which generate random losses for which historical data of ''m'' recent claims are available (indexed by ''j''). A premium for the ''i''th risk is to be determined based on the expected value of claims. A linear estimator which minimizes the mean square error is sought. Write * ''X''ij for the ''j''-th claim on the ''i''-th risk (we assume that all claims for ''i''-th risk are independent and identically distributed Independent or Independents may refer to: Arts, entertainment, and media Artist groups * Independents (artist group), a group of modernist painters based in Pennsylvania, United States * Independ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marginal Likelihood
A marginal likelihood is a likelihood function that has been integrated over the parameter space. In Bayesian statistics, it represents the probability of generating the observed sample for all possible values of the parameters; it can be understood as the probability of the model itself and is therefore often referred to as model evidence or simply evidence. Due to the integration over the parameter space, the marginal likelihood does not directly depend upon the parameters. If the focus is not on model comparison, the marginal likelihood is simply the normalizing constant that ensures that the posterior is a proper probability. It is related to the partition function in statistical mechanics. Concept Given a set of independent identically distributed data points \mathbf=(x_1,\ldots,x_n), where x_i \sim p(x, \theta) according to some probability distribution parameterized by \theta, where \theta itself is a random variable described by a distribution, i.e. \theta \sim p(\t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |