Maxwell Electrodynamics

Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, electric and magnetic circuits.
The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar, etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields.''Electric'' and ''magnetic'' fields, according to the theory of relativity, are the components of a single electromagnetic field. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern form of the equations in their most common formulation is credited to Oliver Heaviside.

Maxwell's equations may be combined to demonstrate how fluctuations in electromagnetic fields (waves) propagate at a constant speed in vacuum, '' c'' (). Known as electromagnetic radiation, these waves occur at various wavelengths to produce a spectrum of radiation from radio waves to gamma rays.

In partial differential equation form and a coherent system of units, Maxwell's microscopic equations can be written as (top to bottom: Gauss's law, Gauss's law for magnetism, Faraday's law, Ampère-Maxwell law)
$\begin \nabla \cdot \mathbf \,\,\, &= \frac \\ \nabla \cdot \mathbf \,\,\, &= 0 \\ \nabla \times \mathbf &= -\frac \\ \nabla \times \mathbf &= \mu_0 \left(\mathbf + \varepsilon_0 \frac \right) \end$
With $\mathbf$ the electric field, $\mathbf$ the magnetic field, $\rho$ the electric charge density and $\mathbf$ the current density. $\varepsilon_0$ is the vacuum permittivity and $\mu_0$ the vacuum permeability.

The equations have two major variants:
* The ''microscopic'' equations have universal applicability but are unwieldy for common calculations. They relate the electric and magnetic fields to total charge and total current, including the complicated charges and currents in materials at the atomic scale.
* The ''macroscopic'' equations define two new auxiliary fields that describe the large-scale behaviour of matter without having to consider atomic-scale charges and quantum phenomena like spins. However, their use requires experimentally determined parameters for a phenomenological description of the electromagnetic response of materials.

The term "Maxwell's equations" is often also used for equivalent alternative formulations. Versions of Maxwell's equations based on the electric and magnetic scalar potentials are preferred for explicitly solving the equations as a boundary value problem, analytical mechanics, or for use in quantum mechanics. The covariant formulation (on spacetime rather than space and time separately) makes the compatibility of Maxwell's equations with special relativity manifest. Maxwell's equations in curved spacetime, commonly used in high-energy and gravitational physics, are compatible with general relativity.In general relativity, however, they must enter, through its stress–energy tensor, into Einstein field equations that include the spacetime curvature. In fact, Albert Einstein developed special and general relativity to accommodate the invariant speed of light, a consequence of Maxwell's equations, with the principle that only relative movement has physical consequences.

The publication of the equations marked the unification of a theory for previously separately described phenomena: magnetism, electricity, light, and associated radiation.
Since the mid-20th century, it has been understood that Maxwell's equations do not give an exact description of electromagnetic phenomena, but are instead a classical limit of the more precise theory of quantum electrodynamics.

History of the equations

Conceptual descriptions

Gauss's law

Gauss's law describes the relationship between an electric field and electric charges: an electric field points away from positive charges and towards negative charges, and the net outflow of the electric field through a closed surface is proportional to the enclosed charge, including bound charge due to polarization of material. The coefficient of the proportion is the permittivity of free space.

Gauss's law for magnetism

Gauss's law for magnetism states that electric charges have no magnetic analogues, called magnetic monopoles; no north or south magnetic poles exist in isolation. Instead, the magnetic field of a material is attributed to a dipole, and the net outflow of the magnetic field through a closed surface is zero. Magnetic dipoles may be represented as loops of current or inseparable pairs of equal and opposite "magnetic charges". Precisely, the total magnetic flux through a Gaussian surface is zero, and the magnetic field is a solenoidal vector field.The absence of sinks/sources of the field does not imply that the field lines must be closed or escape to infinity. They can also wrap around indefinitely, without self-intersections. Moreover, around points where the field is zero (that cannot be intersected by field lines, because their direction would not be defined), there can be the simultaneous begin of some lines and end of other lines. This happens, for instance, in the middle between two identical cylindrical magnets, whose north poles face each other. In the middle between those magnets, the field is zero and the axial field lines coming from the magnets end. At the same time, an infinite number of divergent lines emanate radially from this point. The simultaneous presence of lines which end and begin around the point preserves the divergence-free character of the field. For a detailed discussion of non-closed field lines, see L. Zilbert
"The Misconception of Closed Magnetic Flux Lines"
IEEE Magnetics Letters, vol. 8, art. 1306005, 2017.

Faraday's law

The Maxwell–Faraday version of Faraday's law of induction describes how a time-varying magnetic field corresponds to the negative curl of an electric field. In integral form, it states that the work per unit charge required to move a charge around a closed loop equals the rate of change of the magnetic flux through the enclosed surface.

The electromagnetic induction is the operating principle behind many electric generators: for example, a rotating bar magnet creates a changing magnetic field and generates an electric field in a nearby wire.

Ampère–Maxwell law

The original law of Ampère states that magnetic fields relate to electric current. Maxwell's addition states that magnetic fields also relate to changing electric fields, which Maxwell called displacement current. The integral form states that electric and displacement currents are associated with a proportional magnetic field along any enclosing curve.

Maxwell's modification of Ampère's circuital law is important because the laws of Ampère and Gauss must otherwise be adjusted for static fields. As a consequence, it predicts that a rotating magnetic field occurs with a changing electric field. A further consequence is the existence of self-sustaining electromagnetic waves which travel through empty space.

The speed calculated for electromagnetic waves, which could be predicted from experiments on charges and currents,The quantity we would now call , with units of velocity, was directly measured before Maxwell's equations, in an 1855 experiment by Wilhelm Eduard Weber and Rudolf Kohlrausch. They charged a leyden jar (a kind of capacitor), and measured the electrostatic force associated with the potential; then, they discharged it while measuring the magnetic force from the current in the discharge wire. Their result was , remarkably close to the speed of light. See Joseph F. Keithley
''The story of electrical and magnetic measurements: from 500 B.C. to the 1940s'', p. 115
matches the speed of light; indeed, light ''is'' one form of electromagnetic radiation (as are X-rays, radio waves, and others). Maxwell understood the connection between electromagnetic waves and light in 1861, thereby unifying the theories of electromagnetism and optics.

Formulation in terms of electric and magnetic fields (microscopic or in vacuum version)

In the electric and magnetic field formulation there are four equations that determine the fields for given charge and current distribution. A separate law of nature, the Lorentz force law, describes how the electric and magnetic fields act on charged particles and currents. By convention, a version of this law in the original equations by Maxwell is no longer included. The vector calculus formalism below, the work of Oliver Heaviside, has become standard. It is rotationally invariant, and therefore mathematically more transparent than Maxwell's original 20 equations in ''x'', ''y'' and ''z'' components. The relativistic formulations are more symmetric and Lorentz invariant. For the same equations expressed using tensor calculus or differential forms (see ').

The differential and integral formulations are mathematically equivalent; both are useful. The integral formulation relates fields within a region of space to fields on the boundary and can often be used to simplify and directly calculate fields from symmetric distributions of charges and currents. On the other hand, the differential equations are purely ''local'' and are a more natural starting point for calculating the fields in more complicated (less symmetric) situations, for example using finite element analysis.

Key to the notation

Symbols in bold represent vector quantities, and symbols in ''italics'' represent scalar quantities, unless otherwise indicated.
The equations introduce the electric field, , a vector field, and the magnetic field, , a pseudovector field, each generally having a time and location dependence.
The sources are
* the total electric charge density (total charge per unit volume), , and
* the total electric current density (total current per unit area), .

The universal constants appearing in the equations (the first two ones explicitly only in the SI formulation) are:
* the permittivity of free space, , and
* the permeability of free space, , and
* the speed of light, $c = ()^$

Differential equations

In the differential equations,
*the nabla symbol, , denotes the three-dimensional gradient operator, del,
*the symbol (pronounced "del dot") denotes the divergence operator,
*the symbol (pronounced "del cross") denotes the curl operator.

Integral equations

In the integral equations,
* is any volume with closed boundary surface , and
* is any surface with closed boundary curve ,
The equations are a little easier to interpret with time-independent surfaces and volumes. Time-independent surfaces and volumes are "fixed" and do not change over a given time interval. For example, since the surface is time-independent, we can bring the differentiation under the integral sign in Faraday's law:
$\frac \iint_ \mathbf \cdot \mathrm\mathbf = \iint_ \frac \cdot \mathrm\mathbf\,,$
Maxwell's equations can be formulated with possibly time-dependent surfaces and volumes by using the differential version and using Gauss' and Stokes' theorems as appropriate.
* $_$ is a surface integral over the boundary surface , with the loop indicating the surface is closed
* $\iiint_\Omega$ is a volume integral over the volume ,
* $\oint_$ is a line integral around the boundary curve , with the loop indicating the curve is closed.
* $\iint_\Sigma$ is a surface integral over the surface ,
* The ''total'' electric charge enclosed in is the volume integral over of the charge density (see the "macroscopic formulation" section below): $Q = \iiint_\Omega \rho \ \mathrmV,$ where is the volume element.
* The ''net'' magnetic flux is the surface integral of the magnetic field passing through a fixed surface, : $\Phi_B = \iint_ \mathbf \cdot \mathrm \mathbf,$
* The ''net'' electric flux is the surface integral of the electric field passing through : $\Phi_E = \iint_ \mathbf \cdot \mathrm \mathbf,$
* The ''net'' electric current is the surface integral of the electric current density passing through : $I = \iint_ \mathbf \cdot \mathrm \mathbf,$ where denotes the differential vector element of surface area , normal to surface . (Vector area is sometimes denoted by rather than , but this conflicts with the notation for magnetic vector potential).

Formulation in the SI

Formulation in the Gaussian system

The definitions of charge, electric field, and magnetic field can be altered to simplify theoretical calculation, by absorbing dimensioned factors of and into the units (and thus redefining these). With a corresponding change in the values of the quantities for the Lorentz force law this yields the same physics, i.e. trajectories of charged particles, or work done by an electric motor. These definitions are often preferred in theoretical and high energy physics where it is natural to take the electric and magnetic field with the same units, to simplify the appearance of the electromagnetic tensor: the Lorentz covariant object unifying electric and magnetic field would then contain components with uniform unit and dimension. Such modified definitions are conventionally used with the Gaussian ( CGS) units. Using these definitions, colloquially "in Gaussian units",

the Maxwell equations become:

The equations simplify slightly when a system of quantities is chosen in the speed of light, ''c'', is used for nondimensionalization, so that, for example, seconds and lightseconds are interchangeable, and ''c'' = 1.

Further changes are possible by absorbing factors of . This process, called rationalization, affects whether Coulomb's law or Gauss's law includes such a factor (see ''Heaviside–Lorentz units'', used mainly in particle physics).

Relationship between differential and integral formulations

The equivalence of the differential and integral formulations are a consequence of the Gauss divergence theorem and the Kelvin–Stokes theorem.

Flux and divergence

According to the (purely mathematical) Gauss divergence theorem, the electric flux through the
boundary surface can be rewritten as
: $\vphantom_ \mathbf\cdot\mathrm\mathbf=\iiint_ \nabla\cdot\mathbf\, \mathrmV$
The integral version of Gauss's equation can thus be rewritten as
$\iiint_ \left(\nabla \cdot \mathbf - \frac\right) \, \mathrmV = 0$
Since is arbitrary (e.g. an arbitrary small ball with arbitrary center), this is satisfied if and only if the integrand is zero everywhere. This is
the differential equations formulation of Gauss equation up to a trivial rearrangement.

Similarly rewriting the magnetic flux in Gauss's law for magnetism in integral form gives
: $\vphantom_ \mathbf\cdot\mathrm\mathbf = \iiint_ \nabla \cdot \mathbf\, \mathrmV = 0.$
which is satisfied for all if and only if $\nabla \cdot \mathbf = 0$ everywhere.

Circulation and curl

By the Kelvin–Stokes theorem we can rewrite the line integrals of the fields around the closed boundary curve to an integral of the "circulation of the fields" (i.e. their curls) over a surface it bounds, i.e.
$\oint_ \mathbf \cdot \mathrm\boldsymbol = \iint_\Sigma (\nabla \times \mathbf) \cdot \mathrm\mathbf,$
Hence the Ampère–Maxwell law, the modified version of Ampère's circuital law, in integral form can be rewritten as
$\iint_\Sigma \left(\nabla \times \mathbf - \mu_0 \left(\mathbf + \varepsilon_0 \frac\right)\right)\cdot \mathrm\mathbf = 0.$
Since can be chosen arbitrarily, e.g. as an arbitrary small, arbitrary oriented, and arbitrary centered disk, we conclude that the integrand is zero if and only if the Ampère–Maxwell law in differential equations form is satisfied.
The equivalence of Faraday's law in differential and integral form follows likewise.

The line integrals and curls are analogous to quantities in classical fluid dynamics: the circulation of a fluid is the line integral of the fluid's flow velocity field around a closed loop, and the vorticity of the fluid is the curl of the velocity field.

Charge conservation

The invariance of charge can be derived as a corollary of Maxwell's equations. The left-hand side of the Ampère–Maxwell law has zero divergence by the div–curl identity. Expanding the divergence of the right-hand side, interchanging derivatives, and applying Gauss's law gives:
$0 = \nabla\cdot (\nabla\times \mathbf) = \nabla \cdot \left(\mu_0 \left(\mathbf + \varepsilon_0 \frac \right) \right) = \mu_0\left(\nabla\cdot \mathbf + \varepsilon_0\frac\nabla\cdot \mathbf\right) = \mu_0\left(\nabla\cdot \mathbf +\frac\right)$
i.e.,
$\frac + \nabla \cdot \mathbf = 0.$
By the Gauss divergence theorem, this means the rate of change of charge in a fixed volume equals the net current flowing through the boundary:
: $\fracQ_\Omega = \frac \iiint_ \rho \mathrmV = -$$\vphantom_ \mathbf \cdot \mathbf = - I_.$
In particular, in an isolated system the total charge is conserved.

Vacuum equations, electromagnetic waves and speed of light

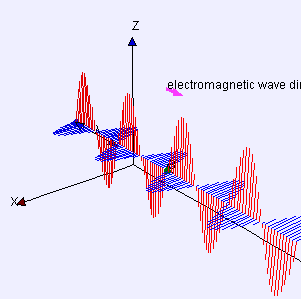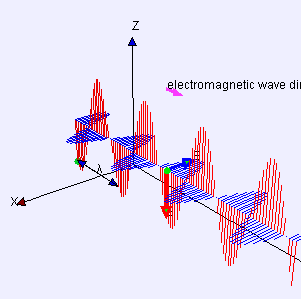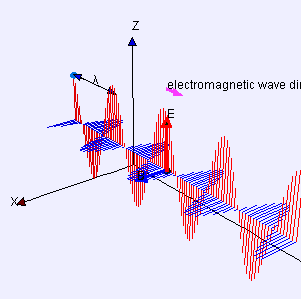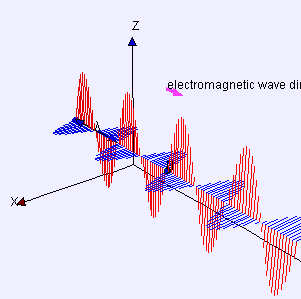
In a region with no charges () and no currents (), such as in vacuum, Maxwell's equations reduce to:
$\begin \nabla \cdot \mathbf &= 0, & \nabla \times \mathbf + \frac = 0, \\ \nabla \cdot \mathbf &= 0, & \nabla \times \mathbf - \mu_0\varepsilon_0 \frac = 0. \end$

Taking the curl of the curl equations, and using the curl of the curl identity we obtain
$\begin \mu_0\varepsilon_0 \frac - \nabla^2 \mathbf = 0, \\ \mu_0\varepsilon_0 \frac - \nabla^2 \mathbf = 0. \end$

The quantity $\mu_0\varepsilon_0$ has the dimension (T/L)². Defining $c = (\mu_0 \varepsilon_0)^$, the equations above have the form of the standard wave equations
$\begin \frac \frac - \nabla^2 \mathbf = 0, \\ \frac \frac - \nabla^2 \mathbf = 0. \end$

Already during Maxwell's lifetime, it was found that the known values for $\varepsilon_0$ and $\mu_0$ give $c \approx 2.998 \times 10^8~\text$, then already known to be the speed of light in free space. This led him to propose that light and radio waves were propagating electromagnetic waves, since amply confirmed. In the old SI system of units, the values of $\mu_0 = 4\pi\times 10^$ and $c = 299\,792\,458~\text$ are defined constants, (which means that by definition $\varepsilon_0 = 8.854\,187\,8... \times 10^~\text$) that define the ampere and the metre. In the new SI system, only ''c'' keeps its defined value, and the electron charge gets a defined value.

In materials with relative permittivity, , and relative permeability, , the phase velocity of light becomes
$v_\text = \frac\sqrt,$
which is usuallyThere are cases ( anomalous dispersion) where the phase velocity can exceed , but the "signal velocity" will still be less than .

In addition, and are perpendicular to each other and to the direction of wave propagation, and are in phase with each other. A sinusoidal plane wave is one special solution of these equations. Maxwell's equations explain how these waves can physically propagate through space. The changing magnetic field creates a changing electric field through Faraday's law. In turn, that electric field creates a changing magnetic field through Maxwell's modification of Ampère's circuital law. This perpetual cycle allows these waves, now known as electromagnetic radiation, to move through space at velocity .

Macroscopic formulation

The above equations are the microscopic version of Maxwell's equations, expressing the electric and the magnetic fields in terms of the (possibly atomic-level) charges and currents present. This is sometimes called the "general" form, but the macroscopic version below is equally general, the difference being one of bookkeeping.

The microscopic version is sometimes called "Maxwell's equations in vacuum": this refers to the fact that the material medium is not built into the structure of the equations, but appears only in the charge and current terms. The microscopic version was introduced by Lorentz, who tried to use it to derive the macroscopic properties of bulk matter from its microscopic constituents.

"Maxwell's macroscopic equations", also known as Maxwell's equations in matter, are more similar to those that Maxwell introduced himself.

In the macroscopic equations, the influence of bound charge and bound current is incorporated into the displacement field and the magnetizing field , while the equations depend only on the free charges and free currents . This reflects a splitting of the total electric charge ''Q'' and current ''I'' (and their densities and J) into free and bound parts:
$\begin Q &= Q_\text + Q_\text = \iiint_\Omega \left(\rho_\text + \rho_\text \right) \, \mathrmV = \iiint_\Omega \rho \,\mathrmV, \\ I &= I_\text + I_\text = \iint_\Sigma \left(\mathbf_\text + \mathbf_\text \right) \cdot \mathrm\mathbf = \iint_\Sigma \mathbf \cdot \mathrm\mathbf. \end$

The cost of this splitting is that the additional fields and need to be determined through phenomenological constituent equations relating these fields to the electric field and the magnetic field , together with the bound charge and current.

See below for a detailed description of the differences between the microscopic equations, dealing with ''total'' charge and current including material contributions, useful in air/vacuum;In some books—e.g., in U. Krey and A. Owen's Basic Theoretical Physics (Springer 2007)—the term ''effective charge'' is used instead of ''total charge'', while ''free charge'' is simply called ''charge''.
and the macroscopic equations, dealing with ''free'' charge and current, practical to use within materials.

Bound charge and current

When an electric field is applied to a dielectric material its molecules respond by forming microscopic electric dipoles – their atomic nuclei move a tiny distance in the direction of the field, while their electrons move a tiny distance in the opposite direction. This produces a ''macroscopic'' ''bound charge'' in the material even though all of the charges involved are bound to individual molecules. For example, if every molecule responds the same, similar to that shown in the figure, these tiny movements of charge combine to produce a layer of positive bound charge on one side of the material and a layer of negative charge on the other side. The bound charge is most conveniently described in terms of the polarization of the material, its dipole moment per unit volume. If is uniform, a macroscopic separation of charge is produced only at the surfaces where enters and leaves the material. For non-uniform , a charge is also produced in the bulk.

Somewhat similarly, in all materials the constituent atoms exhibit magnetic moments that are intrinsically linked to the angular momentum of the components of the atoms, most notably their electrons. The connection to angular momentum suggests the picture of an assembly of microscopic current loops. Outside the material, an assembly of such microscopic current loops is not different from a macroscopic current circulating around the material's surface, despite the fact that no individual charge is traveling a large distance. These '' bound currents'' can be described using the magnetization .

The very complicated and granular bound charges and bound currents, therefore, can be represented on the macroscopic scale in terms of and , which average these charges and currents on a sufficiently large scale so as not to see the granularity of individual atoms, but also sufficiently small that they vary with location in the material. As such, ''Maxwell's macroscopic equations'' ignore many details on a fine scale that can be unimportant to understanding matters on a gross scale by calculating fields that are averaged over some suitable volume.

Auxiliary fields, polarization and magnetization

The ''definitions'' of the auxiliary fields are:
$\begin \mathbf(\mathbf, t) &= \varepsilon_0 \mathbf(\mathbf, t) + \mathbf(\mathbf, t), \\ \mathbf(\mathbf, t) &= \frac \mathbf(\mathbf, t) - \mathbf(\mathbf, t), \end$
where is the polarization field and is the magnetization field, which are defined in terms of microscopic bound charges and bound currents respectively. The macroscopic bound charge density and bound current density in terms of polarization and magnetization are then defined as
$\begin \rho_\text &= -\nabla\cdot\mathbf, \\ \mathbf_\text &= \nabla\times\mathbf + \frac. \end$

If we define the total, bound, and free charge and current density by
$\begin \rho &= \rho_\text + \rho_\text, \\ \mathbf &= \mathbf_\text + \mathbf_\text, \end$
and use the defining relations above to eliminate , and , the "macroscopic" Maxwell's equations reproduce the "microscopic" equations.

Constitutive relations

In order to apply 'Maxwell's macroscopic equations', it is necessary to specify the relations between displacement field and the electric field , as well as the magnetizing field and the magnetic field . Equivalently, we have to specify the dependence of the polarization (hence the bound charge) and the magnetization (hence the bound current) on the applied electric and magnetic field. The equations specifying this response are called constitutive relations. For real-world materials, the constitutive relations are rarely simple, except approximately, and usually determined by experiment. See the main article on constitutive relations for a fuller description.

For materials without polarization and magnetization, the constitutive relations are (by definition)
$\mathbf = \varepsilon_0\mathbf, \quad \mathbf = \frac\mathbf,$
where is the permittivity of free space and the permeability of free space. Since there is no bound charge, the total and the free charge and current are equal.

An alternative viewpoint on the microscopic equations is that they are the macroscopic equations ''together'' with the statement that vacuum behaves like a perfect linear "material" without additional polarization and magnetization.
More generally, for linear materials the constitutive relations are
$\mathbf = \varepsilon\mathbf, \quad \mathbf = \frac\mathbf,$
where is the permittivity and the permeability of the material. For the displacement field the linear approximation is usually excellent because for all but the most extreme electric fields or temperatures obtainable in the laboratory (high power pulsed lasers) the interatomic electric fields of materials of the order of 10¹¹ V/m are much higher than the external field. For the magnetizing field $\mathbf$, however, the linear approximation can break down in common materials like iron leading to phenomena like hysteresis. Even the linear case can have various complications, however.
* For homogeneous materials, and are constant throughout the material, while for inhomogeneous materials they depend on location within the material (and perhaps time).
* For isotropic materials, and are scalars, while for anisotropic materials (e.g. due to crystal structure) they are tensors.
* Materials are generally dispersive, so and depend on the frequency of any incident EM waves.

Even more generally, in the case of non-linear materials (see for example nonlinear optics), and are not necessarily proportional to , similarly or is not necessarily proportional to . In general and depend on both and , on location and time, and possibly other physical quantities.

In applications one also has to describe how the free currents and charge density behave in terms of and possibly coupled to other physical quantities like pressure, and the mass, number density, and velocity of charge-carrying particles. E.g., the original equations given by Maxwell (see ''History of Maxwell's equations'') included Ohm's law in the form
$\mathbf_\text = \sigma \mathbf.$

Alternative formulations

Following are some of the several other mathematical formalisms of Maxwell's equations, with the columns separating the two homogeneous Maxwell equations from the two inhomogeneous ones. Each formulation has versions directly in terms of the electric and magnetic fields, and indirectly in terms of the electrical potential and the vector potential . Potentials were introduced as a convenient way to solve the homogeneous equations, but it was thought that all observable physics was contained in the electric and magnetic fields (or relativistically, the Faraday tensor). The potentials play a central role in quantum mechanics, however, and act quantum mechanically with observable consequences even when the electric and magnetic fields vanish (Aharonov–Bohm effect).

Each table describes one formalism. See the main article for details of each formulation.

The direct spacetime formulations make manifest that the Maxwell equations are relativistically invariant, where space and time are treated on equal footing. Because of this symmetry, the electric and magnetic fields are treated on equal footing and are recognized as components of the Faraday tensor. This reduces the four Maxwell equations to two, which simplifies the equations, although we can no longer use the familiar vector formulation. Maxwell equations in formulation that do not treat space and time manifestly on the same footing have Lorentz invariance as a hidden symmetry. This was a major source of inspiration for the development of relativity theory. Indeed, even the formulation that treats space and time separately is not a non-relativistic approximation and describes the same physics by simply renaming variables. For this reason the relativistic invariant equations are usually called the Maxwell equations as well.

Each table below describes one formalism.

* In the tensor calculus formulation, the electromagnetic tensor is an antisymmetric covariant order 2 tensor; the four-potential, , is a covariant vector; the current, , is a vector; the square brackets, , denote antisymmetrization of indices; is the partial derivative with respect to the coordinate, . In Minkowski space coordinates are chosen with respect to an inertial frame; , so that the metric tensor used to raise and lower indices is . The d'Alembert operator on Minkowski space is as in the vector formulation. In general spacetimes, the coordinate system is arbitrary, the covariant derivative , the Ricci tensor, and raising and lowering of indices are defined by the Lorentzian metric, and the d'Alembert operator is defined as . The topological restriction is that the second real cohomology group of the space vanishes (see the differential form formulation for an explanation). This is violated for Minkowski space with a line removed, which can model a (flat) spacetime with a point-like monopole on the complement of the line.
* In the differential form formulation on arbitrary space times, is the electromagnetic tensor considered as a 2-form, is the potential 1-form, $J = - J_\alpha \mathrmx^\alpha$ is the current 3-form, is the exterior derivative, and $$ is the Hodge star on forms defined (up to its orientation, i.e. its sign) by the Lorentzian metric of spacetime. In the special case of 2-forms such as ''F'', the Hodge star $$ depends on the metric tensor only for its local scale. This means that, as formulated, the differential form field equations are conformally invariant, but the Lorenz gauge condition breaks conformal invariance. The operator $\Box = (- \mathrm \mathrm - \mathrm \mathrm )$ is the d'Alembert–Laplace–Beltrami operator on 1-forms on an arbitrary Lorentzian spacetime. The topological condition is again that the second real cohomology group is 'trivial' (meaning that its form follows from a definition). By the isomorphism with the second de Rham cohomology this condition means that every closed 2-form is exact.

Other formalisms include the geometric algebra formulation and a matrix representation of Maxwell's equations. Historically, a quaternionic formulation was used.

Solutions

Maxwell's equations are partial differential equations that relate the electric and magnetic fields to each other and to the electric charges and currents. Often, the charges and currents are themselves dependent on the electric and magnetic fields via the Lorentz force equation and the constitutive relations. These all form a set of coupled partial differential equations which are often very difficult to solve: the solutions encompass all the diverse phenomena of classical electromagnetism. Some general remarks follow.

As for any differential equation, boundary conditions


and initial conditions
are necessary for a unique solution. For example, even with no charges and no currents anywhere in spacetime, there are the obvious solutions for which E and B are zero or constant, but there are also non-trivial solutions corresponding to electromagnetic waves. In some cases, Maxwell's equations are solved over the whole of space, and boundary conditions are given as asymptotic limits at infinity.
In other cases, Maxwell's equations are solved in a finite region of space, with appropriate conditions on the boundary of that region, for example an artificial absorbing boundary representing the rest of the universe,
or periodic boundary conditions, or walls that isolate a small region from the outside world (as with a waveguide or cavity resonator).

Jefimenko's equations (or the closely related Liénard–Wiechert potentials) are the explicit solution to Maxwell's equations for the electric and magnetic fields created by any given distribution of charges and currents. It assumes specific initial conditions to obtain the so-called "retarded solution", where the only fields present are the ones created by the charges. However, Jefimenko's equations are unhelpful in situations when the charges and currents are themselves affected by the fields they create.

Numerical methods for differential equations can be used to compute approximate solutions of Maxwell's equations when exact solutions are impossible. These include the finite element method and finite-difference time-domain method.


For more details, see Computational electromagnetics.

Overdetermination of Maxwell's equations

Maxwell's equations ''seem'' overdetermined, in that they involve six unknowns (the three components of and ) but eight equations (one for each of the two Gauss's laws, three vector components each for Faraday's and Ampère's circuital laws). (The currents and charges are not unknowns, being freely specifiable subject to charge conservation.) This is related to a certain limited kind of redundancy in Maxwell's equations: It can be proven that any system satisfying Faraday's law and Ampère's circuital law ''automatically'' also satisfies the two Gauss's laws, as long as the system's initial condition does, and assuming conservation of charge and the nonexistence of magnetic monopoles.
This explanation was first introduced by Julius Adams Stratton in 1941.

Although it is possible to simply ignore the two Gauss's laws in a numerical algorithm (apart from the initial conditions), the imperfect precision of the calculations can lead to ever-increasing violations of those laws. By introducing dummy variables characterizing these violations, the four equations become not overdetermined after all. The resulting formulation can lead to more accurate algorithms that take all four laws into account.

Both identities $\nabla\cdot \nabla\times \mathbf \equiv 0, \nabla\cdot \nabla\times \mathbf \equiv 0$, which reduce eight equations to six independent ones, are the true reason of overdetermination.

Equivalently, the overdetermination can be viewed as implying conservation of electric and magnetic charge, as they are required in the derivation described above but implied by the two Gauss's laws.

For linear algebraic equations, one can make 'nice' rules to rewrite the equations and unknowns. The equations can be linearly dependent. But in differential equations, and especially partial differential equations (PDEs), one needs appropriate boundary conditions, which depend in not so obvious ways on the equations. Even more, if one rewrites them in terms of vector and scalar potential, then the equations are underdetermined because of gauge fixing.

Maxwell's equations as the classical limit of QED

Maxwell's equations and the Lorentz force law (along with the rest of classical electromagnetism) are extraordinarily successful at explaining and predicting a variety of phenomena. However, they do not account for quantum effects, and so their domain of applicability is limited. Maxwell's equations are thought of as the classical limit of quantum electrodynamics (QED).

Some observed electromagnetic phenomena cannot be explained with Maxwell's equations if the source of the electromagnetic fields are the classical distributions of charge and current. These include photon–photon scattering and many other phenomena related to photons or virtual photons, "nonclassical light" and quantum entanglement of electromagnetic fields (see ''Quantum optics''). E.g. quantum cryptography cannot be described by Maxwell theory, not even approximately. The approximate nature of Maxwell's equations becomes more and more apparent when going into the extremely strong field regime (see ''Euler–Heisenberg Lagrangian'') or to extremely small distances.

Finally, Maxwell's equations cannot explain any phenomenon involving individual photons interacting with quantum matter, such as the photoelectric effect, Planck's law, the Duane–Hunt law, and single-photon light detectors. However, many such phenomena may be explained using a halfway theory of quantum matter coupled to a classical electromagnetic field, either as external field or with the expected value of the charge current and density on the right hand side of Maxwell's equations. This is known as semiclassical theory or self-field QED and was initially discovered by de Broglie and Schrödinger and later fully developed by E.T. Jaynes and A.O. Barut.

Variations

Popular variations on the Maxwell equations as a classical theory of electromagnetic fields are relatively scarce because the standard equations have stood the test of time remarkably well.

Magnetic monopoles

Maxwell's equations posit that there is electric charge, but no magnetic charge (also called magnetic monopoles), in the universe. Indeed, magnetic charge has never been observed, despite extensive searches,See magnetic monopole for a discussion of monopole searches. Recently, scientists have discovered that some types of condensed matter, including spin ice and topological insulators, display ''emergent'' behavior resembling magnetic monopoles. (Se
sciencemag.org
an

) Although these were described in the popular press as the long-awaited discovery of magnetic monopoles, they are only superficially related. A "true" magnetic monopole is something where , whereas in these condensed-matter systems, while only . and may not exist. If they did exist, both Gauss's law for magnetism and Faraday's law would need to be modified, and the resulting four equations would be fully symmetric under the interchange of electric and magnetic fields.

See also

Explanatory notes

References

Further reading

*

Historical publications

On Faraday's Lines of Force
nbsp;– 1855/56. Maxwell's first paper (Part 1 & 2) – Compiled by Blaze Labs Research (PDF).
* /upload.wikimedia.org/wikipedia/commons/b/b8/On_Physical_Lines_of_Force.pdf On Physical Lines of Forcenbsp;– 1861. Maxwell's 1861 paper describing magnetic lines of force – Predecessor to 1873 Treatise.
* James Clerk Maxwell, "A Dynamical Theory of the Electromagnetic Field", ''Philosophical Transactions of the Royal Society of London'' 155, 459–512 (1865). (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
*
A Dynamical Theory Of The Electromagnetic Field
nbsp;– 1865. Maxwell's 1865 paper describing his 20 equations, link from Google Books.
* J. Clerk Maxwell (1873), "A Treatise on Electricity and Magnetism":
** Maxwell, J. C., "A Treatise on Electricity And Magnetism" �
Volume 1
– 1873 – Posner Memorial Collection – Carnegie Mellon University.
** Maxwell, J. C., "A Treatise on Electricity And Magnetism" �
Volume 2
– 1873 – Posner Memorial Collection – Carnegie Mellon University.

; Developments before the theory of relativity :
*
*
*
* Henri Poincaré (1900) "La théorie de Lorentz et le Principe de Réaction" , ''Archives Néerlandaises'', V, 253–278.
* Henri Poincaré (1902) "La Science et l'Hypothèse" .
* Henri Poincaré (1905
"Sur la dynamique de l'électron"
, ''Comptes Rendus de l'Académie des Sciences'', 140, 1504–1508.
* Catt, Walton and Davidson

. ''Wireless World'', March 1979.

External links

*

maxwells-equations.com
— An intuitive tutorial of Maxwell's equations.


* Wikiversity Page on Maxwell's Equations

Modern treatments

Electromagnetism (ch. 11)
B. Crowell, Fullerton College


R. Fitzpatrick, University of Texas at Austin

''Electromagnetic waves from Maxwell's equations''
o
Project PHYSNET



Taught by Professor Walter Lewin.

Other

*

{{DEFAULTSORT:Maxwell's Equations

Electromagnetism
Eponymous equations of physics
Functions of space and time
James Clerk Maxwell
Partial differential equations
Scientific laws