|
Work (physics)
In science, work is the energy transferred to or from an Physical object, object via the application of force along a Displacement (vector), displacement. In its simplest form, for a constant force aligned with the direction of motion, the work equals the Product (mathematics), product of the force strength and the distance traveled. A force is said to do ''positive work'' if it has a component in the direction of the displacement of the point of application. A force does ''negative work'' if it has a component opposite to the direction of the displacement at the point of application of the force. For example, when a ball is held above the ground and then dropped, the work done by the gravitational force on the ball as it falls is positive, and is equal to the weight of the ball (a force) multiplied by the distance to the ground (a displacement). If the ball is thrown upwards, the work done by the gravitational force is negative, and is equal to the weight multiplied by the dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Baseball Pitching Motion 2004
Baseball is a bat-and-ball games, bat-and-ball sport played between two team sport, teams of nine players each, taking turns batting (baseball), batting and Fielding (baseball), fielding. The game occurs over the course of several Pitch (baseball), plays, with each play beginning when a player on the fielding team (baseball), fielding team, called the pitcher, throws a Baseball (ball), ball that a player on the batting team (baseball), batting team, called the Batter (baseball), batter, tries to hit with a baseball bat, bat. The objective of the offensive team (batting team) is to hit the ball into the field of play, away from the other team's players, allowing its players to run the Base (baseball), bases, having them advance counter-clockwise around four bases to score what are called "Run (baseball), runs". The objective of the defensive team (referred to as the fielding team) is to prevent batters from becoming Base running, runners, and to prevent runners base running ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector (mathematics And Physics)
In mathematics and physics, vector is a term that refers to physical quantity, quantities that cannot be expressed by a single number (a scalar (physics), scalar), or to elements of some vector spaces. Historically, vectors were introduced in geometry and physics (typically in mechanics) for quantities that have both a magnitude and a direction, such as displacement (geometry), displacements, forces and velocity. Such quantities are represented by geometric vectors in the same way as distances, masses and time are represented by real numbers. The term ''vector'' is also used, in some contexts, for tuples, which are finite sequences (of numbers or other objects) of a fixed length. Both geometric vectors and tuples can be added and scaled, and these vector operations led to the concept of a vector space, which is a set (mathematics), set equipped with a vector addition and a scalar multiplication that satisfy some axioms generalizing the main properties of operations on the abov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gottfried Wilhelm Leibniz
Gottfried Wilhelm Leibniz (or Leibnitz; – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat who is credited, alongside Sir Isaac Newton, with the creation of calculus in addition to many other branches of mathematics, such as binary arithmetic and statistics. Leibniz has been called the "last universal genius" due to his vast expertise across fields, which became a rarity after his lifetime with the coming of the Industrial Revolution and the spread of specialized labor. He is a prominent figure in both the history of philosophy and the history of mathematics. He wrote works on philosophy, theology, ethics, politics, law, history, philology, games, music, and other studies. Leibniz also made major contributions to physics and technology, and anticipated notions that surfaced much later in probability theory, biology, medicine, geology, psychology, linguistics and computer science. Leibniz contributed to the field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramount to his method of inquiry, and he connected the previously separate fields of geometry and algebra into analytic geometry. Descartes spent much of his working life in the Dutch Republic, initially serving the Dutch States Army, and later becoming a central intellectual of the Dutch Golden Age. Although he served a Dutch Reformed Church, Protestant state and was later counted as a Deism, deist by critics, Descartes was Roman Catholicism, Roman Catholic. Many elements of Descartes's philosophy have precedents in late Aristotelianism, the Neostoicism, revived Stoicism of the 16th century, or in earlier philosophers like Augustine of Hippo, Augustine. In his natural philosophy, he differed from the Scholasticism, schools on two major point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642), commonly referred to as Galileo Galilei ( , , ) or mononymously as Galileo, was an Italian astronomer, physicist and engineer, sometimes described as a polymath. He was born in the city of Pisa, then part of the Duchy of Florence. Galileo has been called the father of observational astronomy, modern-era classical physics, the scientific method, and modern science. Galileo studied speed and velocity, gravity and free fall, the principle of relativity, inertia, projectile motion and also worked in applied science and technology, describing the properties of the pendulum and "hydrostatic balances". He was one of the earliest Renaissance developers of the thermoscope and the inventor of various sector (instrument), military compasses. With an improved telescope he built, he observed the stars of the Milky Way, the phases of Venus, the Galilean moons, four largest satellites of Jupiter, Saturn's r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
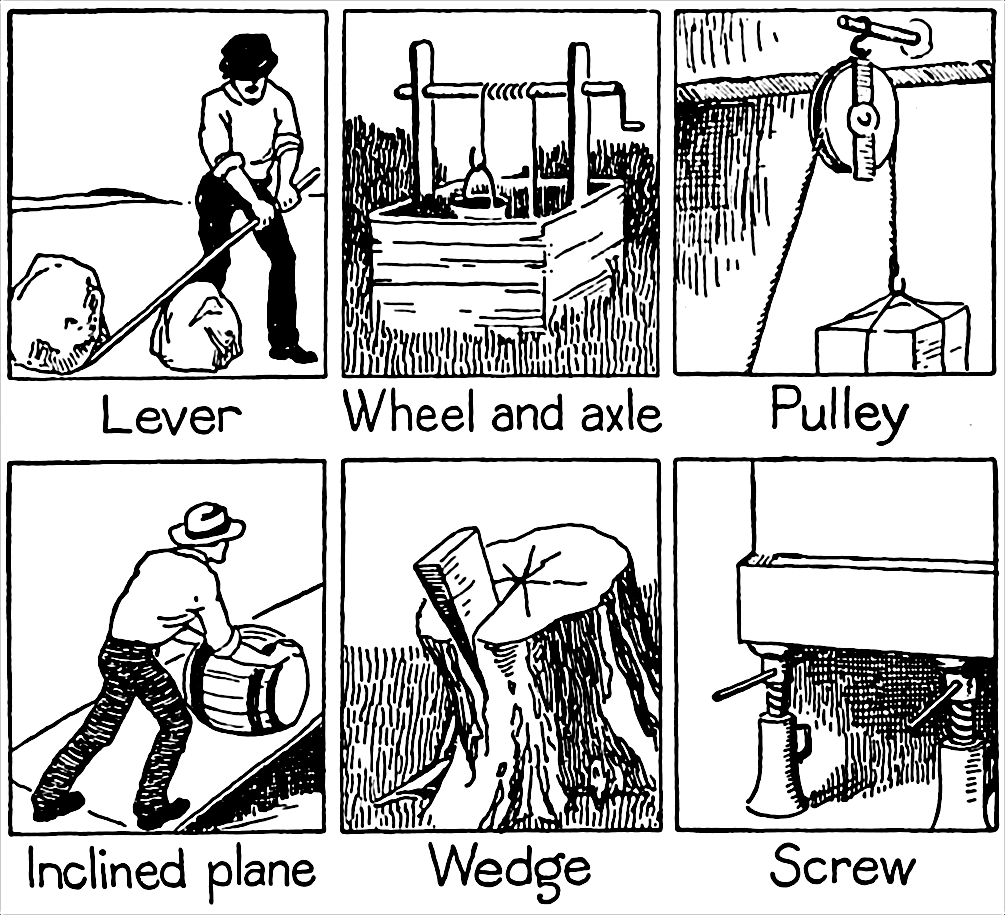
Simple Machine
A simple machine is a machine, mechanical device that changes the Direction (geometry) , direction or Magnitude_(mathematics) , magnitude of a force. In general, they can be defined as the simplest Mechanism (engineering) , mechanisms that use mechanical advantage (also called leverage) to multiply force. Usually the term refers to the six classical simple machines that were defined by Renaissance scientists: * Lever * Wheel and axle * Pulley * Inclined plane * Wedge (mechanical device), Wedge * Screw (simple machine), Screw A simple machine uses a single applied force to do Mechanical work, work against a single load force. Ignoring friction losses, the work done on the load is equal to the work done by the applied force. The machine can increase the amount of the output force, at the cost of a proportional decrease in the distance moved by the load. The ratio of the output to the applied force is called the ''mechanical advantage''. Simple machines can be regarded as the eleme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Renaissance
The Renaissance ( , ) is a Periodization, period of history and a European cultural movement covering the 15th and 16th centuries. It marked the transition from the Middle Ages to modernity and was characterized by an effort to revive and surpass the ideas and achievements of classical antiquity. Associated with great social change in most fields and disciplines, including Renaissance art, art, Renaissance architecture, architecture, politics, Renaissance literature, literature, Renaissance exploration, exploration and Science in the Renaissance, science, the Renaissance was first centered in the Republic of Florence, then spread to the Italian Renaissance, rest of Italy and later throughout Europe. The term ''rinascita'' ("rebirth") first appeared in ''Lives of the Artists'' () by Giorgio Vasari, while the corresponding French word was adopted into English as the term for this period during the 1830s. The Renaissance's intellectual basis was founded in its version of Renaiss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamics (mechanics)
In physics, dynamics or classical dynamics is the study of forces and their effect on motion. It is a branch of classical mechanics, along with ''statics'' and ''kinematics''. The ''fundamental principle of dynamics'' is linked to Newton's second law. Subdivisions Rigid bodies Fluids Applications Classical dynamics finds many applications: * ''Aerodynamics'', the study of the motion of air * '' Brownian dynamics'', the occurrence of Langevin dynamics in the motion of particles in solution * '' File dynamics'', stochastic motion of particles in a channel * ''Flight dynamics'', the science of aircraft and spacecraft design * ''Molecular dynamics'', the study of motion on the molecular level * '' Langevin dynamics'', a mathematical model for stochastic dynamics * '' Orbital dynamics'', the study of the motion of rockets and spacecraft * '' Stellar dynamics'', a description of the collective motion of stars * '' Vehicle dynamics, the study of vehicles in motion Generalizations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statics
Statics is the branch of classical mechanics that is concerned with the analysis of force and torque acting on a physical system that does not experience an acceleration, but rather is in mechanical equilibrium, equilibrium with its environment. If \textbf F is the total of the forces acting on the system, m is the mass of the system and \textbf a is the acceleration of the system, Newton's second law states that \textbf F = m \textbf a \, (the bold font indicates a Euclidean vector, vector quantity, i.e. one with both Magnitude (mathematics), magnitude and Direction (geometry), direction). If \textbf a =0, then \textbf F = 0. As for a system in static equilibrium, the acceleration equals zero, the system is either at rest, or its center of mass moves at constant velocity. The application of the assumption of zero acceleration to the summation of Moment (physics), moments acting on the system leads to \textbf M = I \alpha = 0, where \textbf M is the summation of all momen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ancient Greek Technology
Ancient Greek technology developed during the 5th century BC, continuing up to and including the Roman period, and beyond. Inventions that are credited to the ancient Greeks include the gear, screw, rotary mills, bronze casting techniques, water clock, water organ, the torsion catapult, the use of steam to operate some experimental machines and toys, and a chart to find prime numbers. Many of these inventions occurred late in the Greek period, often inspired by the need to improve weapons and tactics in war. However, peaceful uses are shown by their early development of the watermill, a device which pointed to further exploitation on a large scale under the Romans. They developed surveying and mathematics to an advanced state, and many of their technical advances were published by philosophers, like Archimedes and Heron. Water technology Some fields that were encompassed in the area of water resources (mainly for urban use) included groundwater exploitation, construction of aqued ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SI Unit
The International System of Units, internationally known by the abbreviation SI (from French ), is the modern form of the metric system and the world's most widely used system of units of measurement, system of measurement. It is the only system of measurement with official status in nearly every country in the world, employed in science, technology, industry, and everyday commerce. The SI system is coordinated by the International Bureau of Weights and Measures, which is abbreviated BIPM from . The SI comprises a coherence (units of measurement), coherent system of unit of measurement, units of measurement starting with seven SI base unit, base units, which are the second (symbol s, the unit of time), metre (m, length), kilogram (kg, mass), ampere (A, electric current), kelvin (K, thermodynamic temperature), mole (unit), mole (mol, amount of substance), and candela (cd, luminous intensity). The system can accommodate coherent units for an unlimited number of additional quantiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar (physics)
Scalar quantities or simply scalars are physical quantities that can be described by a single pure number (a ''scalar'', typically a real number), accompanied by a unit of measurement, as in "10cm" (ten centimeters). Examples of scalar are length, mass, charge, volume, and time. Scalars may represent the magnitude of physical quantities, such as speed is to velocity. Scalars do not represent a direction. Scalars are unaffected by changes to a vector space basis (i.e., a coordinate rotation) but may be affected by translations (as in relative speed). A change of a vector space basis changes the description of a vector in terms of the basis used but does not change the vector itself, while a scalar has nothing to do with this change. In classical physics, like Newtonian mechanics, rotations and reflections preserve scalars, while in relativity, Lorentz transformations or space-time translations preserve scalars. The term "scalar" has origin in the multiplication o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |