fractional integral

Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator $D$
:$D f(x) = \frac f(x)\,,$

and of the integration operator $J$ The symbol $J$ is commonly used instead of the intuitive $I$ in order to avoid confusion with other concepts identified by similar $I$–like glyphs, such as identities.
:$J f(x) = \int_0^x f(s) \,ds\,,$

and developing a calculus for such operators generalizing the classical one.

In this context, the term ''powers'' refers to iterative application of a linear operator $D$ to a function $f$, that is, repeatedly composing $D$ with itself, as in $D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots)))$.

For example, one may ask for a meaningful interpretation of
:$\sqrt = D^\frac12$

as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to any function, will have the same effect as differentiation. More generally, one can look at the question of defining a linear operator
:$D^a$

for every real number $a$ in such a way that, when $a$ takes an integer value $n\in\mathbb$, it coincides with the usual $n$-fold differentiation $D$ if $n>0$, and with the $n$-th power of $J$ when $n<0$.

One of the motivations behind the introduction and study of these sorts of extensions of the differentiation operator $D$ is that the sets of operator powers $\$ defined in this way are ''continuous'' semigroups with parameter $a$, of which the original ''discrete'' semigroup of $\$ for integer $n$ is a denumerable subgroup: since continuous semigroups have a well developed mathematical theory, they can be applied to other branches of mathematics.

Fractional differential equations, also known as extraordinary differential equations, are a generalization of differential equations through the application of fractional calculus.

Historical notes

In applied mathematics and mathematical analysis, a fractional derivative is a derivative of any arbitrary order, real or complex. Its first appearance is in a letter written to Guillaume de l'Hôpital by Gottfried Wilhelm Leibniz in 1695.  Around the same time, Leibniz wrote to one of the Bernoulli brothers describing the similarity between the binomial theorem and the Leibniz rule for the fractional derivative of a product of two functions.  Fractional calculus was introduced in one of Niels Henrik Abel's early papers where all the elements can be found: the idea of fractional-order integration and differentiation, the mutually inverse relationship between them, the understanding that fractional-order differentiation and integration can be considered as the same generalized operation, and even the unified notation for differentiation and integration of arbitrary real order.
Independently, the foundations of the subject were laid by Liouville in a paper from 1832.
The autodidact Oliver Heaviside introduced the practical use of fractional differential operators in electrical transmission line analysis circa 1890. The theory and applications of fractional calculus expanded greatly over the 19th and 20th centuries, and numerous contributors have given different definitions for fractional derivatives and integrals.

Nature of the fractional derivative

The $a$-th derivative of a function $f$ at a point $x$ is a ''local property'' only when $a$ is an integer; this is not the case for non-integer power derivatives. In other words, a non-integer fractional derivative of $f$ at $x=a$ depends on all values of $f$, even those far away from $a$. Therefore, it is expected that the fractional derivative operation involves some sort of boundary conditions, involving information on the function further out.

The fractional derivative of a function of order $a$ is nowadays often defined by means of the Fourier or Mellin integral transforms.

Heuristics

A fairly natural question to ask is whether there exists a linear operator , or half-derivative, such that
:$H^2 f(x) = D f(x) = \dfrac f(x) = f'(x) \,.$

It turns out that there is such an operator, and indeed for any , there exists an operator such that
:$\left(P ^ a f\right)(x) = f'(x),$

or to put it another way, the definition of can be extended to all real values of .

Let be a function defined for . Form the definite integral from 0 to . Call this
:$( J f ) ( x ) = \int_0^x f(t) \, dt \,.$

Repeating this process gives
:$\left( J^2 f \right) (x) = \int_0^x (Jf)(t) \,dt = \int_0^x \left(\int_0^t f(s) \,ds \right) dt \,,$
and this can be extended arbitrarily.

The Cauchy formula for repeated integration, namely
:$\left(J^n f\right) ( x ) = \frac \int_0^x \left(x-t\right)^ f(t) \, dt \,,$
leads in a straightforward way to a generalization for real .

Using the gamma function to remove the discrete nature of the factorial function gives us a natural candidate for fractional applications of the integral operator.
:$\left(J^\alpha f\right) ( x ) = \frac \int_0^x \left(x-t\right)^ f(t) \, dt \,.$

This is in fact a well-defined operator.

It is straightforward to show that the operator satisfies
:$\left(J^\alpha\right) \left(J^\beta f\right)(x) = \left(J^\beta\right) \left(J^\alpha f\right)(x) = \left(J^ f\right)(x) = \frac \int_0^x \left(x-t\right)^ f(t) \, dt \,.$

This relationship is called the semigroup property of fractional differintegral operators. Unfortunately, the comparable process for the derivative operator is significantly more complex, but it can be shown that is neither commutative nor additive in general.

Fractional integrals

Riemann–Liouville fractional integral

The classical form of fractional calculus is given by the Riemann–Liouville integral, which is essentially what has been described above. The theory of fractional integration for periodic functions (therefore including the "boundary condition" of repeating after a period) is given by the Weyl integral. It is defined on Fourier series, and requires the constant Fourier coefficient to vanish (thus, it applies to functions on the unit circle whose integrals evaluate to zero). The Riemann–Liouville integral exists in two forms, upper and lower. Considering the interval , the integrals are defined as
:$_aD_t^ f(t)=_aI_t^\alpha f(t)=\frac\int_a^t \left(t-\tau\right)^ f(\tau) \, d\tau$
:$_tD_b^ f(t)=_tI_b^\alpha f(t)=\frac\int_t^b \left(\tau-t\right)^ f(\tau) \, d\tau$

Where the former is valid for and the latter is valid for .

By contrast the Grünwald–Letnikov derivative starts with the derivative instead of the integral.

Hadamard fractional integral

The ''Hadamard fractional integral'' was introduced by Jacques Hadamard and is given by the following formula,
:$_a\mathbf_t^ f(t) = \frac \int_a^t \left(\log\frac \right)^ f(\tau)\frac, \qquad t > a\,.$

Atangana–Baleanu fractional integral

The Atangana–Baleanu fractional integral of a continuous function is defined as:
:$^_aI_t^\alpha f(t)=\fracf(t)+\frac\int_a^t \left(t-\tau\right)^ f(\tau) \, d\tau$

Fractional derivatives

Unlike classical Newtonian derivatives, fractional derivatives can be defined in a variety of different ways that often do not all lead to the same result even for smooth functions. Some of these are defined via a fractional integral. Because of the incompatibility of definitions, it is frequently necessary to be explicit about which definition is used.

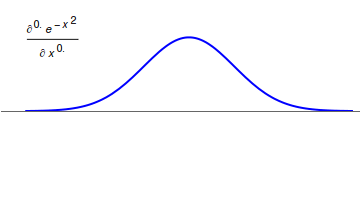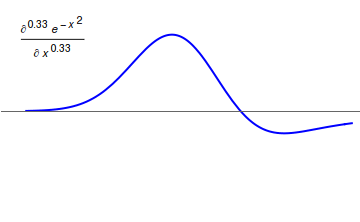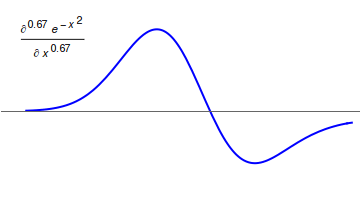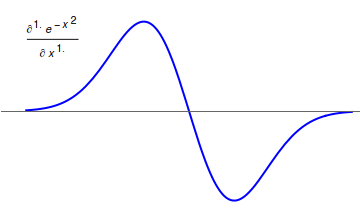
Riemann–Liouville fractional derivative

The corresponding derivative is calculated using Lagrange's rule for differential operators. Computing th order derivative over the integral of order , the order derivative is obtained. It is important to remark that is the smallest integer greater than (that is, ). Similar to the definitions for the Riemann–Liouville integral, the derivative has upper and lower variants.
:$_aD_t^\alpha f(t)=\frac _aD_t^f(t)=\frac _aI_t^ f(t)$
:$_tD_b^\alpha f(t)=\frac _tD_b^f(t)=\frac _tI_b^ f(t)$

Caputo fractional derivative

Another option for computing fractional derivatives is the Caputo fractional derivative. It was introduced by Michele Caputo in his 1967 paper. In contrast to the Riemann–Liouville fractional derivative, when solving differential equations using Caputo's definition, it is not necessary to define the fractional order initial conditions. Caputo's definition is illustrated as follows, where again :
:$^C D_t^\alpha f(t)=\frac \int_0^t \frac\, d\tau.$

There is the Caputo fractional derivative defined as:
: D^\nu f(t)=\frac \int_0^t (t-u)^f^(u)\, du \qquad (n-1)<\nu
which has the advantage that is zero when is constant and its Laplace Transform is expressed by means of the initial values of the function and its derivative. Moreover, there is the Caputo fractional derivative of distributed order defined as
:_a^b D^\nu f(t)=\int_a^b \phi(\nu)\left ^f(t)\right,d\nu=\int_a^b\left frac\int_0^t \left(t-u\right)^f'(u)\,du \right,d\nu
where is a weight function and which is used to represent mathematically the presence of multiple memory formalisms.

Caputo–Fabrizio fractional derivative

In a paper of 2015, M. Caputo and M. Fabrizio presented a definition of fractional derivative with a non singular kernel, for a function $f(t)$ of $C^1$ given by:
:$_a^ D_t^\alpha f(t)=\frac \int_a^t f'(\tau) \ e^\left(-\alpha\frac\right) \ d\tau,$

where $a < 0, \alpha \in (0,1]$

Atangana–Baleanu fractional derivative

In 2016, Atangana and Baleanu suggested differential operators based on the generalized Mittag-Leffler function. The aim was to introduce fractional differential operators with non-singular nonlocal kernel. Their fractional differential operators are given below in Riemann–Liouville sense and Caputo sense respectively. For a function $f(t)$ of $C^1$ given by
:$_a^ D_t^\alpha f(t)=\frac \int_a^t f'(\tau)E_\left(-\alpha\frac\right)d\tau,$

If the function is continuous, the Atangana–Baleanu derivative in Riemann–Liouville sense is given by:
:$_a^ D_t^\alpha f(t)=\frac \frac\int_a^t f(\tau)E_\left(-\alpha\frac\right)d\tau,$

The kernel used in Atangana–Baleanu fractional derivative has some properties of a cumulative distribution function.  For example, for all $\alpha \in (0, 1]$, the function $E_\alpha$ is increasing on the real line, converges to $0$ in $- \infty$, and $E_\alpha (0) = 1$. Therefore, we have that, the function $x \mapsto 1-E_\alpha (-x^\alpha)$ is the cumulative distribution function of a probability measure on the positive real numbers. The distribution is therefore defined, and any of its multiples, is called a Mittag-Leffler distribution of order $\alpha$. It is also very well-known that, all these probability distributions are absolutely continuous. In particular, the function Mittag-Leffler has a particular case $E_1$, which is the exponential function, the Mittag-Leffler distribution of order $1$ is therefore an exponential distribution. However, for $\alpha \in (0, 1)$, the Mittag-Leffler distributions are heavy-tailed. Their Laplace transform is given by:
:$\mathbb (e^) = \frac,$

This directly implies that, for $\alpha \in (0, 1)$, the expectation is infinite. In addition, these distributions are geometric stable distributions.

Riesz derivative

The Riesz derivative is defined as
:$\mathcal \left\(k) = -\left, k\^ \mathcal \(k),$

where $\mathcal$ denotes the Fourier transform.

Other types

Classical fractional derivatives include:
* Grünwald–Letnikov derivative
* Sonin–Letnikov derivative
* Liouville derivative
* Caputo derivative
* Hadamard derivative
* Marchaud derivative
* Riesz derivative
* Miller–Ross derivative
* Weyl derivative
* Erdélyi–Kober derivative
* $F^$-derivative
New fractional derivatives include:
* Coimbra derivative
* Katugampola derivative
* Hilfer derivative
* Davidson derivative
* Chen derivative
* Caputo Fabrizio derivative
* Atangana–Baleanu derivative

Generalizations

Erdélyi–Kober operator

The Erdélyi–Kober operator is an integral operator introduced by Arthur Erdélyi (1940). and Hermann Kober (1940) and is given by
:$\frac\int_0^x \left(t-x\right)^t^f(t) \,dt\,,$

which generalizes the Riemann–Liouville fractional integral and the Weyl integral.

Functional calculus

In the context of functional analysis, functions more general than powers are studied in the functional calculus of spectral theory. The theory of pseudo-differential operators also allows one to consider powers of . The operators arising are examples of singular integral operators; and the generalisation of the classical theory to higher dimensions is called the theory of Riesz potentials. So there are a number of contemporary theories available, within which ''fractional calculus'' can be discussed. See also Erdélyi–Kober operator, important in special function theory , .

Applications

Fractional conservation of mass

As described by Wheatcraft and Meerschaert (2008), a fractional conservation of mass equation is needed to model fluid flow when the control volume is not large enough compared to the scale of heterogeneity and when the flux within the control volume is non-linear. In the referenced paper, the fractional conservation of mass equation for fluid flow is:
:$-\rho \left(\nabla^\alpha \cdot \vec \right) = \Gamma(\alpha +1)\Delta x^ \rho \left (\beta_s+\phi \beta_w \right ) \frac$

Electrochemical analysis

When studying the redox behavior of a substrate in solution, a voltage is applied at an electrode surface to force electron transfer between electrode and substrate. The resulting electron transfer is measured as a current. The current depends upon the concentration of substrate at the electrode surface. As substrate is consumed, fresh substrate diffuses to the electrode as described by Fick's laws of diffusion. Taking the Laplace transform of Fick's second law yields an ordinary second-order differential equation (here in dimensionless form):
:$\frac C(x,s) = sC(x,s)$

whose solution C(x,s) contains a one-half power dependence on s. Taking the derivative of C(x,s) and then the inverse Laplace transform yields the following relationship:
:$\frac C(x,t) = \fracC(x,t)$

which relates the concentration of substrate at the electrode surface to the current. This relationship is applied in electrochemical kinetics to elucidate mechanistic behavior. For example, it has been used to study the rate of dimerization of substrates upon electrochemical reduction.

Groundwater flow problem

In 2013–2014 Atangana et al. described some groundwater flow problems using the concept of a derivative with fractional order. In these works, the classical Darcy law is generalized by regarding the water flow as a function of a non-integer order derivative of the piezometric head. This generalized law and the law of conservation of mass are then used to derive a new equation for groundwater flow.

Fractional advection dispersion equation

This equation has been shown useful for modeling contaminant flow in heterogenous porous media.

Atangana and Kilicman extended the fractional advection dispersion equation to a variable order equation. In their work, the hydrodynamic dispersion equation was generalized using the concept of a variational order derivative. The modified equation was numerically solved via the Crank–Nicolson method. The stability and convergence in numerical simulations showed that the modified equation is more reliable in predicting the movement of pollution in deformable aquifers than equations with constant fractional and integer derivatives

Time-space fractional diffusion equation models

Anomalous diffusion processes in complex media can be well characterized by using fractional-order diffusion equation models. The time derivative term corresponds to long-time heavy tail decay and the spatial derivative for diffusion nonlocality. The time-space fractional diffusion governing equation can be written as
:$\frac=-K (-\Delta)^\beta u.$

A simple extension of the fractional derivative is the variable-order fractional derivative, and are changed into and . Its applications in anomalous diffusion modeling can be found in the reference.

Structural damping models

Fractional derivatives are used to model viscoelastic damping in certain types of materials like polymers.

PID controllers

Generalizing PID controllers to use fractional orders can increase their degree of freedom. The new equation relating the ''control variable'' in terms of a measured ''error value'' can be written as
:$u(t) = K_\mathrm e(t) + K_\mathrm D_t^ e(t) + K_\mathrm D_t^ e(t)$

where and are positive fractional orders and , , and , all non-negative, denote the coefficients for the proportional, integral, and derivative terms, respectively (sometimes denoted , , and ).

Acoustic wave equations for complex media

The propagation of acoustical waves in complex media, such as in biological tissue, commonly implies attenuation obeying a frequency power-law. This kind of phenomenon may be described using a causal wave equation which incorporates fractional time derivatives:
:$\nabla^2 u -\dfrac 1 \frac + \tau_\sigma^\alpha \dfrac\nabla^2 u - \dfrac \dfrac = 0\,.$

See also Holm & Näsholm (2011) and the references therein. Such models are linked to the commonly recognized hypothesis that multiple relaxation phenomena give rise to the attenuation measured in complex media. This link is further described in Näsholm & Holm (2011b) and in the survey paper, as well as the '' Acoustic attenuation'' article. See Holm & Nasholm (2013) for a paper which compares fractional wave equations which model power-law attenuation. This book on power-law attenuation also covers the topic in more detail.

Pandey and Holm gave a physical meaning to fractional differential equations by deriving them from physical principles and interpreting the fractional-order in terms of the parameters of the acoustical media, example in fluid-saturated granular unconsolidated marine sediments. Interestingly, Pandey and Holm derived Lomnitz's law in seismology and Nutting's law in non-Newtonian rheology using the framework of fractional calculus. Nutting's law was used to model the wave propagation in marine sediments using fractional derivatives.

Fractional Schrödinger equation in quantum theory

The fractional Schrödinger equation, a fundamental equation of fractional quantum mechanics, has the following form:
:$i\hbar \frac=D_ \left(-\hbar^2\Delta \right)^\psi (\mathbf,t)+V(\mathbf,t)\psi (\mathbf,t)\,.$

where the solution of the equation is the wavefunction – the quantum mechanical probability amplitude for the particle to have a given position vector at any given time , and is the reduced Planck constant. The potential energy function depends on the system.

Further, is the Laplace operator, and is a scale constant with physical dimension , (at , for a particle of mass ), and the operator is the 3-dimensional fractional quantum Riesz derivative defined by
:$(-\hbar^2\Delta)^\frac\psi (\mathbf,t) = \frac 1 \int d^3 p e^, \mathbf, ^\alpha \varphi (\mathbf,t) \,.$

The index in the fractional Schrödinger equation is the Lévy index, .

Variable-order fractional Schrödinger equation

As a natural generalization of the fractional Schrödinger equation, the variable-order fractional Schrödinger equation has been exploited to study fractional quantum phenomena:
:$i\hbar \frac = \left(-\hbar^2\Delta \right)^\psi (\mathbf,t)+V(\mathbf,t)\psi (\mathbf,t),$

where is the Laplace operator and the operator is the variable-order fractional quantum Riesz derivative.

See also

* Acoustic attenuation
* Autoregressive fractionally integrated moving average
* Initialized fractional calculus
* Nonlocal operator

Other fractional theories

* Fractional-order system
* Fractional Fourier transform

Notes

References

Further reading

Articles regarding the history of fractional calculus

*
*
*
*
*

Books

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

External links

* From MathWorld:
**
**
**
*
* Specialized journals

Fractional Calculus and Applied Analysis
1998–2014

Fractional Calculus and Applied Analysis
2015—

Fractional Differential Calculus (FDC)
2011–

Communications in Fractional Calculus


Journal of Fractional Calculus and Applications (JFCA)
2011—
*
*
* collection of books, articles, preprints, etc.
*
*

Fractional Calculus Modelling

Introductory Notes on Fractional Calculus



The CRONE Toolbox
a Matlab and Simulink Toolbox dedicated to fractional calculus, which is freely downloadable
*
*

{{Authority control

Generalizations