|
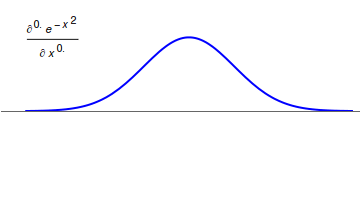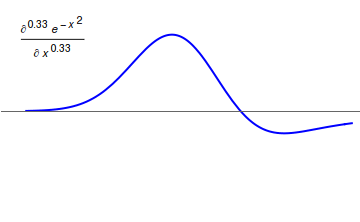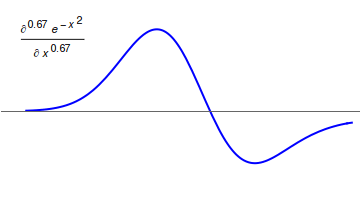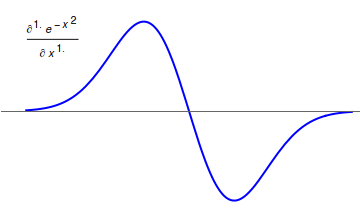
Grünwald–Letnikov Derivative
In mathematics, the Grünwald–Letnikov derivative is a basic extension of the derivative in fractional calculus that allows one to take the derivative a non-integer number of times. It was introduced by Anton Karl Grünwald (1838–1920) from Prague, in 1867, and by Aleksey Vasilievich Letnikov (1837–1888) in Moscow in 1868. Constructing the Grünwald–Letnikov derivative The formula :f'(x) = \lim_ \frac for the derivative can be applied recursively to get higher-order derivatives. For example, the second-order derivative would be: :\beginf''(x)&=\lim_\frac\\&=\lim_\frac\end Assuming that the ''h'' 's converge synchronously, this simplifies to: : = \lim_ \frac which can be justified rigorously by the mean value theorem. In general, we have (see binomial coefficient In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers and is writte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar glyphs, such as identities. J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function that is, repeatedly composing D with itself, as in \begin D^n(f) &= (\underbrace_n)(f) \\ &= \underbrace_n (f)\cdots))). \end For example, one may ask for a meaningful interpretation of \sqrt = D^ as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied to any f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anton Karl Grünwald
Anton may refer to: People *Anton (given name), a list of people with the given name *Anton (surname), a list of people with the surname Places *Anton Municipality, Bulgaria **Anton, Sofia Province, a village *Antón District, Panama **Antón, a town and capital of the district *Anton, Colorado, an unincorporated town *Anton, Texas, a city *Anton, Wisconsin, an unincorporated community *River Anton, Hampshire, United Kingdom Other uses *Case Anton, codename for the German and Italian occupation of Vichy France in 1942 *Anton (computer), a highly parallel supercomputer for molecular dynamics simulations * ''Anton'' (1973 film), a Norwegian film * ''Anton'' (2008 film), an Irish film * Anton Cup, the championship trophy of the Swedish junior hockey league J20 SuperElit * Dynamite Anton, an name of the main protagonist of Antonblast, a 2024 video game and Antonball Deluxe ''Antonball Deluxe'', stylized in all caps, is a 2021 Puzzle video game, puzzle-Breakout clone, brick b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prague
Prague ( ; ) is the capital and List of cities and towns in the Czech Republic, largest city of the Czech Republic and the historical capital of Bohemia. Prague, located on the Vltava River, has a population of about 1.4 million, while its Prague metropolitan area, metropolitan area is home to approximately 2.3 million people. Prague is a historical city with Romanesque architecture, Romanesque, Czech Gothic architecture, Gothic, Czech Renaissance architecture, Renaissance and Czech Baroque architecture, Baroque architecture. It was the capital of the Kingdom of Bohemia and residence of several Holy Roman Emperors, most notably Charles IV, Holy Roman Emperor, Charles IV (r. 1346–1378) and Rudolf II, Holy Roman Emperor, Rudolf II (r. 1575–1611). It was an important city to the Habsburg monarchy and Austria-Hungary. The city played major roles in the Bohemian Reformation, Bohemian and the Protestant Reformations, the Thirty Years' War and in 20th-century history a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aleksey Letnikov
Aleksey Vasilyevich Letnikov (, 1837–1888) was a Russian mathematician. After graduating from the Konstantinovsky Land-Surveying Institute () in Moscow, Letnikov attended classes at Moscow University and the Sorbonne. In 1860 he became an Instructor of Mathematics at the Konstantinovsky Institute. He obtained the degrees of Master and Ph.D. from Moscow University in 1868 and 1874 respectively. In 1868 Letnikov became a professor at the Imperial Moscow Technical School and from 1879 to 1880 was an Inspector at the school. From 1883 he was the principal of the Aleksandrov Commercial School (, currently The State University of Managementbr>and from 1884 he was a Corresponding Member of the Russian Academy of Sciences. His most renowned contribution to mathematics was the creation of the Grünwald–Letnikov derivative. He also published results in the fields of analytic geometry, ordinary differential equations, and non-Euclidean geometry. Letnikov died in Moscow in 1888 an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moscow
Moscow is the Capital city, capital and List of cities and towns in Russia by population, largest city of Russia, standing on the Moskva (river), Moskva River in Central Russia. It has a population estimated at over 13 million residents within the city limits, over 19.1 million residents in the urban area, and over 21.5 million residents in Moscow metropolitan area, its metropolitan area. The city covers an area of , while the urban area covers , and the metropolitan area covers over . Moscow is among the world's List of largest cities, largest cities, being the List of European cities by population within city limits, most populous city entirely in Europe, the largest List of urban areas in Europe, urban and List of metropolitan areas in Europe, metropolitan area in Europe, and the largest city by land area on the European continent. First documented in 1147, Moscow became the capital of the Grand Principality of Moscow, which led the unification of the Russian lan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Value Theorem
In mathematics, the mean value theorem (or Lagrange's mean value theorem) states, roughly, that for a given planar arc (geometry), arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant line, secant through its endpoints. It is one of the most important results in real analysis. This theorem is used to prove statements about a function on an interval (mathematics), interval starting from local hypotheses about derivatives at points of the interval. History A special case of this theorem for inverse interpolation of the sine was first described by Parameshvara (1380–1460), from the Kerala School of Astronomy and Mathematics in India, in his commentaries on Govindasvāmi and Bhāskara II. A restricted form of the theorem was proved by Michel Rolle in 1691; the result was what is now known as Rolle's theorem, and was proved only for polynomials, without the techniques of calculus. The mean value theorem in its modern for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Coefficient
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers and is written \tbinom. It is the coefficient of the term in the polynomial expansion of the binomial power ; this coefficient can be computed by the multiplicative formula : \binom nk = \frac, which using factorial notation can be compactly expressed as : \binom = \frac. For example, the fourth power of is : \begin (1 + x)^4 &= \tbinom x^0 + \tbinom x^1 + \tbinom x^2 + \tbinom x^3 + \tbinom x^4 \\ &= 1 + 4x + 6 x^2 + 4x^3 + x^4, \end and the binomial coefficient \tbinom =\tfrac = \tfrac = 6 is the coefficient of the term. Arranging the numbers \tbinom, \tbinom, \ldots, \tbinom in successive rows for gives a triangular array called Pascal's triangle, satisfying the recurrence relation : \binom = \binom + \binom . The binomial coefficients occur in many areas of mathematics, and espe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |