|
Mittag-Leffler Function
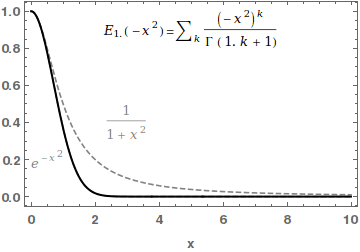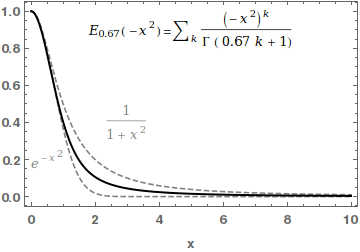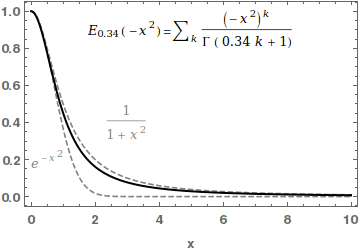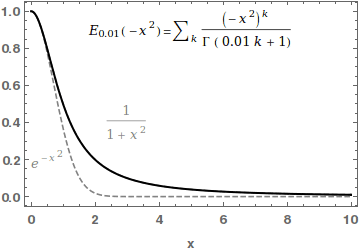
In mathematics, the Mittag-Leffler functions are a family of special functions. They are complex-valued functions of a complex argument ''z'', and moreover depend on one or two complex parameters. The one-parameter Mittag-Leffler function, introduced by Gösta Mittag-Leffler in 1903,Haubold,H J and Mathai,A M and Saxena,R KJ Appl Math 2011, 298628/ref> can be defined by the Maclaurin series :E_ (z) = \sum_^\infty \frac, where \Gamma(x) is the gamma function, and \alpha is a complex parameter with \operatorname\left(\alpha \right)> 0. The two-parameter Mittag-Leffler function, introduced by Wiman in 1905, is occasionally called the generalized Mittag-Leffler function. It has an additional complex parameter \beta, and may be defined by the series :E_ (z) = \sum_^\infty \frac, When \beta=1, the one-parameter function E_\alpha = E_ is recovered. In the case \alpha and \beta are real and positive, the series converges for all values of the argument z, so the Mittag-Leffler fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and Data and information visualization, data visualization. It has been widely adopted in the fields of data mining, bioinformatics, data analysis, and data science. The core R language is extended by a large number of R package, software packages, which contain Reusability, reusable code, documentation, and sample data. Some of the most popular R packages are in the tidyverse collection, which enhances functionality for visualizing, transforming, and modelling data, as well as improves the ease of programming (according to the authors and users). R is free and open-source software distributed under the GNU General Public License. The language is implemented primarily in C (programming language), C, Fortran, and Self-hosting (compilers), R itself. Preprocessor, Precompiled executables are available for the major operating systems (including Linux, MacOS, and Microsoft Windows). Its core is an interpreted language with a na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mittag-Leffler Distribution
The Mittag-Leffler distributions are two families of probability distributions on the half-line ,\infty). They are parametrized by a real \alpha \in (0, 1/math> or \alpha \in , 1/math>. Both are defined with the Mittag-Leffler function, named after Gösta Mittag-Leffler. The Mittag-Leffler function For any complex \alpha whose real part is positive, the series :E_\alpha (z) := \sum_^\infty \frac defines an entire function. For \alpha = 0, the series converges only on a disc of radius one, but it can be analytically extended to \mathbb \setminus \. First family of Mittag-Leffler distributions The first family of Mittag-Leffler distributions is defined by a relation between the Mittag-Leffler function and their cumulative distribution functions. For all \alpha \in (0, 1], the function E_\alpha is increasing on the real line, converges to 0 in - \infty, and E_\alpha (0) = 1. Hence, the function x \mapsto 1-E_\alpha (-x^\alpha) is the cumulative distribution function of a probab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Series
In mathematics, a power series (in one variable) is an infinite series of the form \sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a constant called the ''center'' of the series. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function. In many situations, the center ''c'' is equal to zero, for instance for Maclaurin series. In such cases, the power series takes the simpler form \sum_^\infty a_n x^n = a_0 + a_1 x + a_2 x^2 + \dots. The partial sums of a power series are polynomials, the partial sums of the Taylor series of an analytic function are a sequence of converging polynomial approximations to the function at the center, and a converging power series can be seen as a kind of generalized polynom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Linear Solid Model
The standard linear solid (SLS), also known as the Zener model after Clarence Zener, is a method of modeling the behavior of a viscoelastic material using a linear combination of springs and dashpots to represent elastic and viscous components, respectively. Often, the simpler Maxwell model and the Kelvin–Voigt model are used. These models often prove insufficient, however; the Maxwell model does not describe creep or recovery, and the Kelvin–Voigt model does not describe stress relaxation. SLS is the simplest model that predicts both phenomena. Definition Materials undergoing strain are often modeled with mechanical components, such as springs (restorative force component) and dashpots (damping component). Connecting a spring and damper in series yields a model of a Maxwell material while connecting a spring and damper in parallel yields a model of a Kelvin–Voigt material.David Roylance, "Engineering Viscoelasticity" (October 24, 2001) https://ocw.mit.edu/course ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscoelasticity
In materials science and continuum mechanics, viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like water, resist both shear flow and strain linearly with time when a stress is applied. Elastic materials strain when stretched and immediately return to their original state once the stress is removed. Viscoelastic materials have elements of both of these properties and, as such, exhibit time-dependent strain. Whereas elasticity is usually the result of bond stretching along crystallographic planes in an ordered solid, viscosity is the result of the diffusion of atoms or molecules inside an amorphous material.Meyers and Chawla (1999): "Mechanical Behavior of Materials", 98-103. Background In the nineteenth century, physicists such as James Clerk Maxwell, Ludwig Boltzmann, and Lord Kelvin researched and experimented with creep and recovery of glasses, metals, and rubbers. Viscoel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pochhammer Symbol
In mathematics, the falling factorial (sometimes called the descending factorial, falling sequential product, or lower factorial) is defined as the polynomial \begin (x)_n = x^\underline &= \overbrace^ \\ &= \prod_^n(x-k+1) = \prod_^(x-k) . \end The rising factorial (sometimes called the Pochhammer function, Pochhammer polynomial, ascending factorial, — A reprint of the 1950 edition by Chelsea Publishing. rising sequential product, or upper factorial) is defined as \begin x^ = x^\overline &= \overbrace^ \\ &= \prod_^n(x+k-1) = \prod_^(x+k) . \end The value of each is taken to be 1 (an empty product) when n=0. These symbols are collectively called factorial powers. The Pochhammer symbol, introduced by Leo August Pochhammer, is the notation (x)_n, where is a non-negative integer. It may represent ''either'' the rising or the falling factorial, with different articles and authors using different conventions. Pochhammer himself actually used (x)_n with yet another meaning, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prabhakar Function
Prabhakar function is a certain special function in mathematics introduced by the Indian mathematician Tilak Raj Prabhakar in a paper published in 1971. The function is a three-parameter generalization of the well known two-parameter Mittag-Leffler function in mathematics. The function was originally introduced to solve certain classes of integral equations. Later the function was found to have applications in the theory of fractional calculus and also in certain areas of physics. Definition The one-parameter and two-parameter Mittag-Leffler functions are defined first. Then the definition of the three-parameter Mittag-Leffler function, the Prabhakar function, is presented. In the following definitions, \Gamma (z) is the well known gamma function defined by ::\Gamma(z)= \int_0^\infty t^e^\, dz, \quad\Re(z) > 0. In the following it will be assumed that \alpha, \beta and \gamma are all complex numbers. One-parameter Mittag-Leffler function The one-parameter Mittag-Leffler func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mittag-Leffler Summation
In mathematics, Mittag-Leffler summation is any of several variations of the Borel summation method for summing possibly divergent formal power series, introduced by Definition Let :y(z) = \sum_^\infty y_kz^k be a formal power series in ''z''. Define the transform \scriptstyle \mathcal_\alpha y of \scriptstyle y by :\mathcal_\alpha y(t) \equiv \sum_^\infty \fract^k Then the Mittag-Leffler sum of ''y'' is given by :\lim_\mathcal_\alpha y( z) if each sum converges and the limit exists. A closely related summation method, also called Mittag-Leffler summation, is given as follows . Suppose that the Borel transform \mathcal_1 y(z) converges to an analytic function near 0 that can be analytically continued along the positive real axis to a function growing sufficiently slowly that the following integral is well defined (as an improper integral). Then the Mittag-Leffler sum of ''y'' is given by :\int_0^\infty e^ \mathcal_\alpha y(t^\alpha z) \, dt When ''α'' = 1 this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex-valued frequency domain, also known as ''s''-domain, or ''s''-plane). The transform is useful for converting derivative, differentiation and integral, integration in the time domain into much easier multiplication and Division (mathematics), division in the Laplace domain (analogous to how logarithms are useful for simplifying multiplication and division into addition and subtraction). This gives the transform many applications in science and engineering, mostly as a tool for solving linear differential equations and dynamical systems by simplifying ordinary differential equations and integral equations into algebraic equation, algebraic polynomial equations, and by simplifyin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Cosine
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions are used to express the angle of parallelism in hyperbolic geometry. They are used to express Lorentz boosts as hyperbolic rotations in special relativity. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, and fluid dynamics. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictionary'', p. 32 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |