fluxion (mathematics)

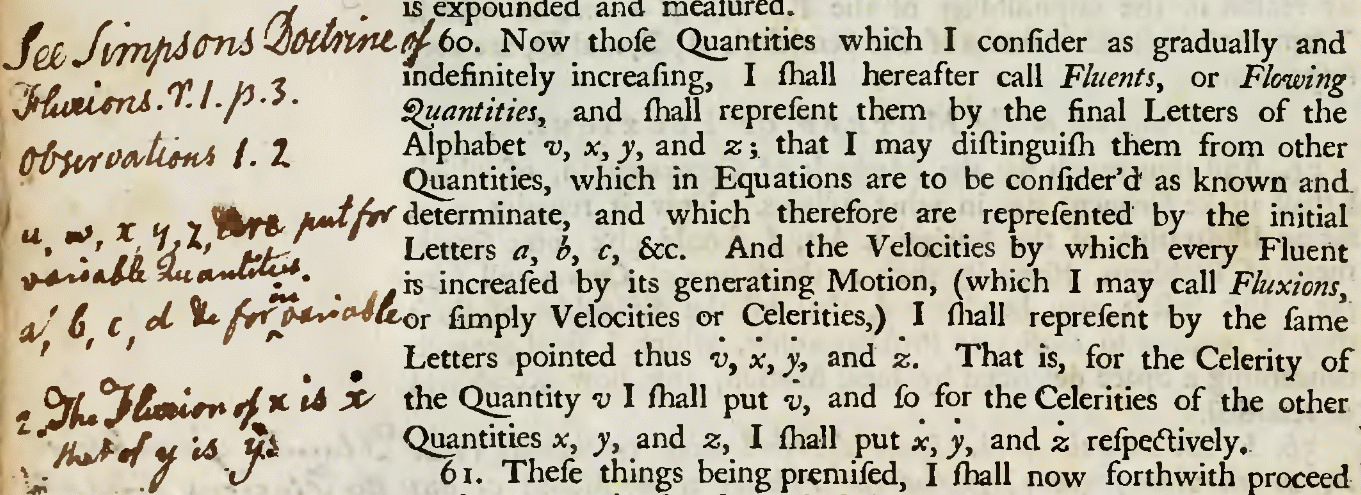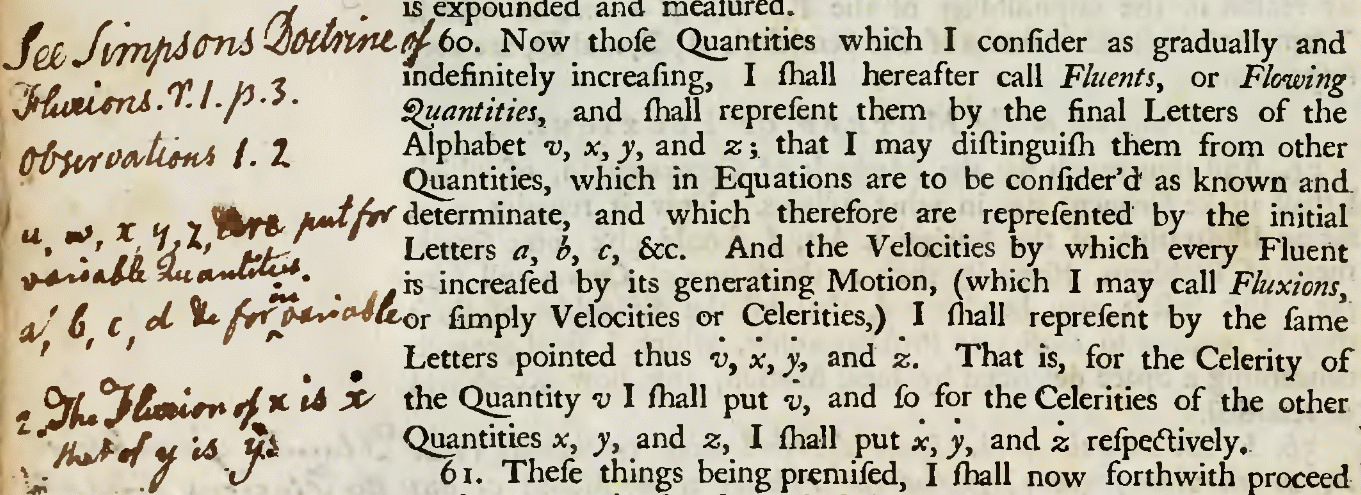A fluxion is the instantaneous rate of change, or gradient, of a fluent (a time-varying quantity, or function) at a given point. Fluxions were introduced by Isaac Newton to describe his form of a time derivative (a derivative with respect to time). Newton introduced the concept in 1665 and detailed them in his mathematical treatise, '' Method of Fluxions''. Fluxions and fluents made up Newton's early calculus.

History

Fluxions were central to the Leibniz–Newton calculus controversy, when Newton sent a letter to Gottfried Wilhelm Leibniz explaining them, but concealing his words in code due to his suspicion. He wrote:

The gibberish string was in fact a hash code (by denoting the frequency of each letter) of the Latin phrase ''Data æqvatione qvotcvnqve flventes qvantitates involvente, flvxiones invenire: et vice versa'', meaning: "Given an equation that consists of any number of flowing quantities, to find the fluxions: and vice versa".

Example

If the fluent is defined as $y=t^2$ (where is time) the fluxion (derivative) at $t=2$ is:
:$\dot y = \frac = \frac = \frac = \frac$
Here is an infinitely small amount of time. So, the term is second order infinite small term and according to Newton, we can now ignore because of its second order infinite smallness comparing to first order infinite smallness of . So, the final equation gets the form:
:$\dot y = \frac=\frac=4$
He justified the use of as a non-zero quantity by stating that fluxions were a consequence of movement by an object.

Criticism

Bishop George Berkeley, a prominent philosopher of the time, denounced Newton's fluxions in his essay ''The Analyst'', published in 1734. Berkeley refused to believe that they were accurate because of the use of the infinitesimal . He did not believe it could be ignored and pointed out that if it was zero, the consequence would be division by zero. Berkeley referred to them as "ghosts of departed quantities", a statement which unnerved mathematicians of the time and led to the eventual disuse of infinitesimals in calculus.

Towards the end of his life Newton revised his interpretation of as infinitely small, preferring to define it as approaching zero, using a similar definition to the concept of limit. He believed this put fluxions back on safe ground. By this time, Leibniz's derivative (and his notation) had largely replaced Newton's fluxions and fluents, and remains in use today.

See also

*History of calculus
* Newton's notation
*Hyperreal number: A modern formalization of the reals that includes infinity and infinitesimals
*Nonstandard analysis

References

{{Isaac Newton, state=collapsed
Mathematical analysis
Differential calculus
History of calculus